Contexto del Proyecto
La integración arquitectónica de energía solar es tendencia, pero conlleva riesgos si no se calcula bien. Anda Gestión Global S.L., responsable del Odalys Campus en Sevilla, detectó anomalías visuales en su instalación de paneles tras un tiempo de operación.
Estas deficiencias sugerían un incumplimiento de los estándares de seguridad del Código Técnico de la Edificación (CTE).
Ante esta situación, se vuelve imperativa una validación estructural de fachada PV. En Atreydes Ingeniería hemos asumido el control técnico. Nuestro objetivo es determinar si la configuración instalada es segura para los estudiantes y la estructura. Para ello, empleamos la avanzada metodología de los elementos finitos (FEM).
Este caso real ilustra la importancia de nuestro servicio de cálculo estructural para diagnosticar y prevenir patologías en edificaciones existentes.

Proceso de validación estructural de fachada PV
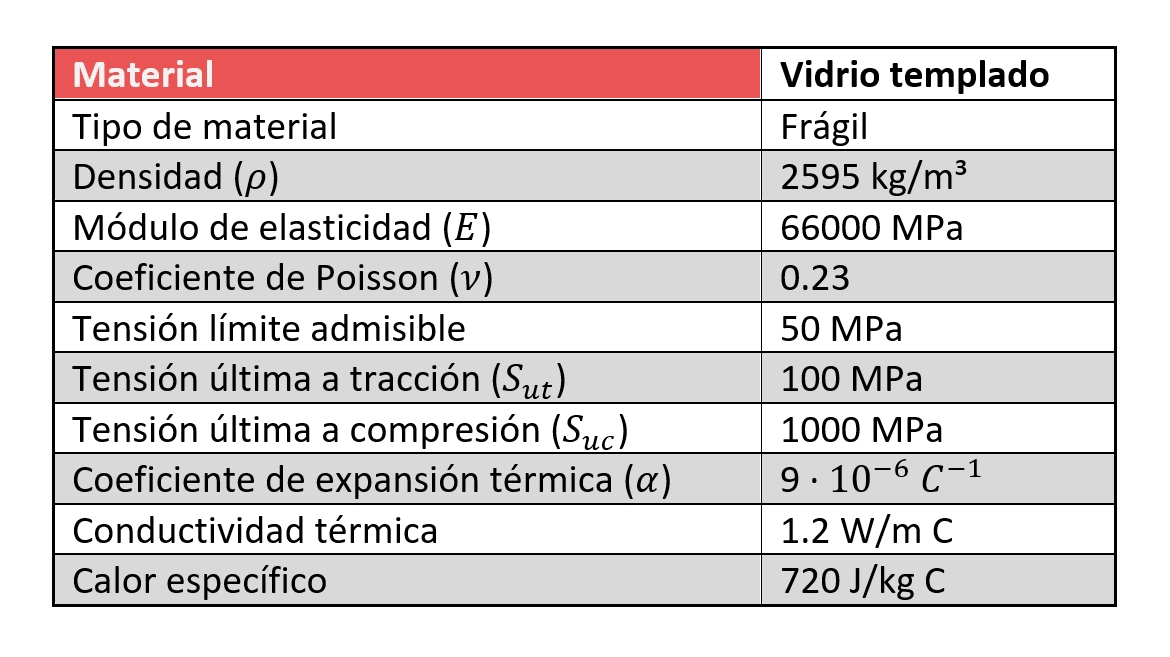
Para ejecutar la validación estructural de fachada PV, comenzamos digitalizando la geometría real. Los paneles son de vidrio templado. El formato más grande es de 1800x600x10 mm, instalados en posición vertical (modo retrato).
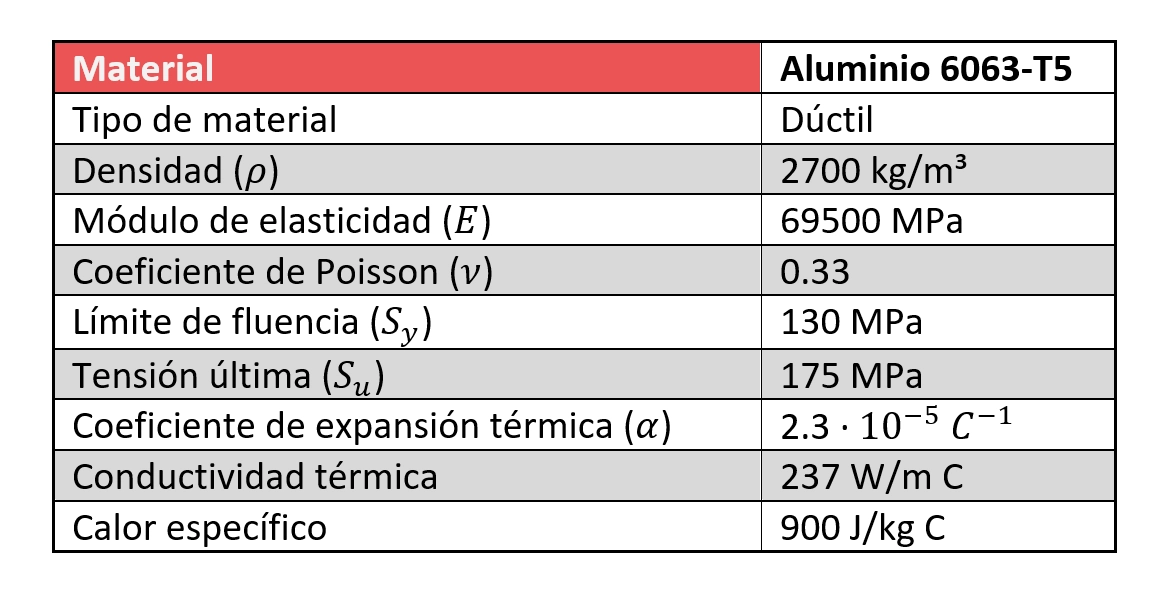
El sistema de fijación es el punto neurálgico. Los paneles apoyan sobre guías verticales de aluminio (aleación 6063-T5). Se sujetan por sus lados cortos mediante dos grapas de aluminio atornilladas a las guías.
La carga viaja de las guías a la pared a través de anclajes en L. Aseguramos todo el conjunto con tornillería tirafondo. Si un eslabón falla, la validación estructural de fachada PV será negativa.
A continuación, presentamos el modelo de estudio generado.
La unidad debe resistir su peso propio y, sobre todo, el viento. En esta fachada, la succión del viento es más crítica que la compresión. Por seguridad, basamos el cálculo en la succión.
En el modelo FEM, usamos elementos «shell» para el vidrio y anclajes en L (espesor constante). Usamos elementos «solid» para las guías complejas. Esta precisión es vital para una validación estructural de fachada PV fiable.
El fallo no siempre es una rotura visible; a veces es una deformación permanente que inutiliza la pieza. En ingeniería distinguimos entre comportamiento dúctil (se deforma antes de romper) y frágil (rompe súbitamente).
Los materiales dúctiles tienen una deformación a rotura ( \epsilon_f ) > 0.05. Los frágiles se definen por su resistencia última a tracción ( S_{ut} ).
Materiales dúctiles
Para la validación estructural de fachada PV en elementos de aluminio, aplicamos Von Mises ( \sigma_{VM} ). El componente es seguro si la tensión no supera el límite elástico reducido por un coeficiente ( \gamma ):
\sigma_{VM} \leq S_y' = \Large \frac{S_y}{\gamma}
Donde:
- \sigma_{MV} : tensión de von Mises
- S_y : límite de fluencia
- \gamma : coeficiente de seguridad (1.05)
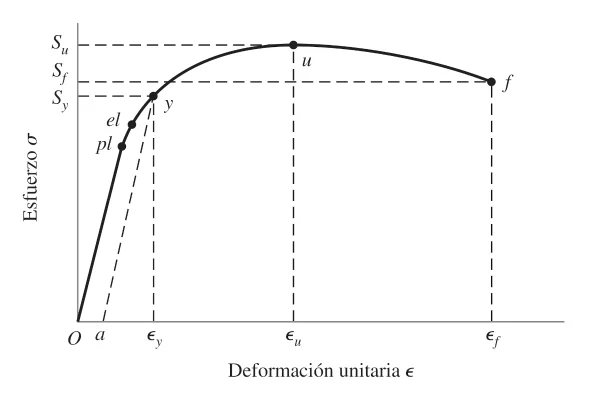
La tensión de Von Mises predice cuándo el material empieza a ceder plásticamente:
\sigma_{MV} = \sqrt{\Large \frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}}
Asumimos un comportamiento lineal (Ley de Hooke) para simplificar el cálculo en rango elástico:
\sigma = E \epsilon; \forall \epsilon < \epsilon_y
\epsilon_y = \Large \frac{\sigma_y}{E}
Con:
- E : módulo elástico
- \epsilon : deformación unitaria
- \sigma : tensión
Donde:
- S_y : límite de fluencia
- S_u : límite de resistencia
- S_f : límite de rotura
En 3D, la fórmula se desarrolla así:
\sigma_{MV} = \sqrt{\Large \frac{(\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+6 (\tau_x^2+\tau_y^2+\tau_z^2)}{2}}
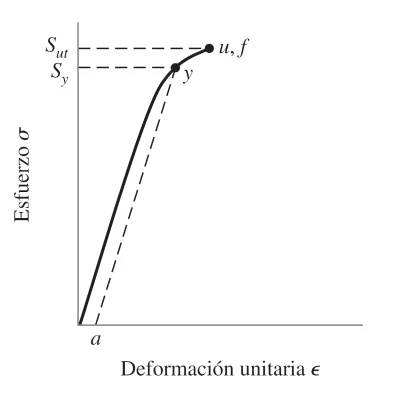
Materiales frágiles
El vidrio sigue la teoría del esfuerzo normal máximo.
Falla si \sigma_1 \geq S_{ut} o \sigma_3 \leq -S_{uc} .
En nuestra validación estructural de fachada PV, verificamos el vidrio templado con:
\sigma_{MV} \leq \Large \frac {1}{\gamma} \normalsize min (S_{ut}, S_{uc})
Donde S_{ut} y S_{uc} son los límites de rotura a tracción y compresión.
La calidad de los materiales es fundamental para el éxito de la validación estructural de fachada PV. En este proyecto intervienen:
- Aluminio 6063-T5: Elemento estructural (guías, grapas, anclajes).
- Vidrio templado: Elemento de captación solar.
Además del peso propio, la carga determinante es el viento. Para el cálculo, aplicamos estrictamente el Código Técnico de la Edificación (CTE).
Cálculo según CTE
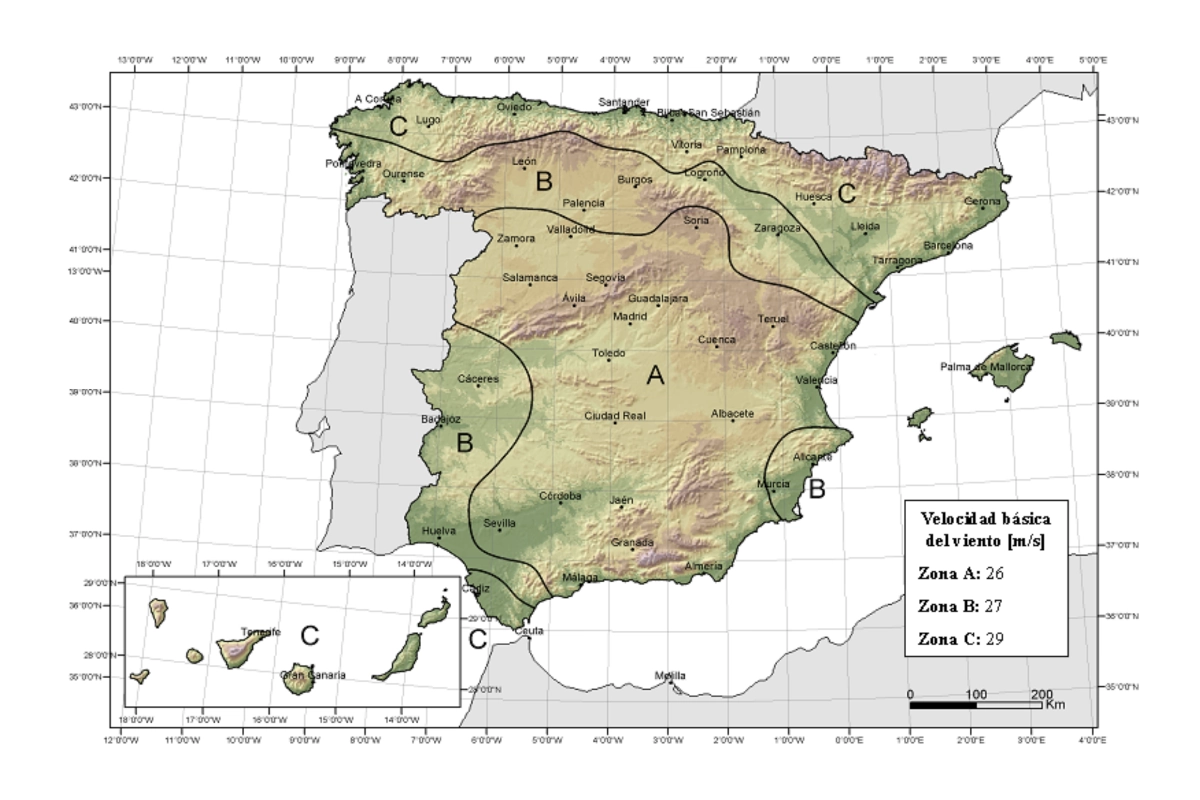
La velocidad básica ( v_b ) en Sevilla es 26m/s.
La presión dinámica ( w ) se calcula como:
w = q_{ref} C_e(z) C_p
Siendo q_{ref} = \Large \frac{1}{2}\normalsize \rho v_b^2 con densidad del aire 1.25kg/m³.
El coeficiente de exposición ( C_e ) para 18m de altura en terreno tipo IV es 2.20.
Según la tabla D3 del CTE, para áreas >10m², el coeficiente de succión ( C_p ) es -1.2. Este valor es más desfavorable que la presión (0.8).
Finalmente, mayoramos la carga con un coeficiente de seguridad ( \gamma ) de 1.5. La carga final aplicada en la validación estructural de fachada PV es:
P_v = 1.5 · \Large \frac{1}{2}\normalsize · 1.25 · 26^2 · 2.2 · (-1.2) = -1673 N/mm^2
Resultados del análisis
Los mapas de tensiones confirman las sospechas iniciales. Se observa una flexión excesiva en el vidrio templado. Aunque el vidrio resiste, el problema grave está en las fijaciones.
Al sujetar los paneles solo por el lado corto, la carga no se distribuye bien. Las guías de aluminio no logran transferir el esfuerzo a la pared por los anclajes intermedios. Esto sobrecarga críticamente los anclajes de los extremos.
Las zonas en color blanco indican que se ha superado el límite elástico (fluencia). Esto implica deformación permanente. En una validación estructural de fachada PV, esto es inaceptable. Las grapas de sujeción son insuficientes para soportar la succión del viento de cálculo.
Conclusiones
La configuración actual (paneles verticales con guías verticales) incumple el Código Técnico de la Edificación (CTE). Existe riesgo real de colapso o daños severos en las fijaciones.
La solución técnica pasa por cambiar la disposición a horizontal. Esto permitiría fijar los paneles por su lado largo, reduciendo la luz de 1800mm a 600mm. Así, la carga se repartiría entre más puntos de anclaje de forma homogénea.
Este estudio demuestra que la validación estructural de fachada PV es indispensable antes y durante la explotación. Un mal diseño compromete la inversión y la seguridad.
Si tienes dudas sobre la integridad de tu edificio, consulta otros casos en nuestro portafolio de proyectos. Para un diagnóstico experto inmediato, contacta con Atreydes Ingeniería.
















