Pérdida de carga en placas delgadas perforadas
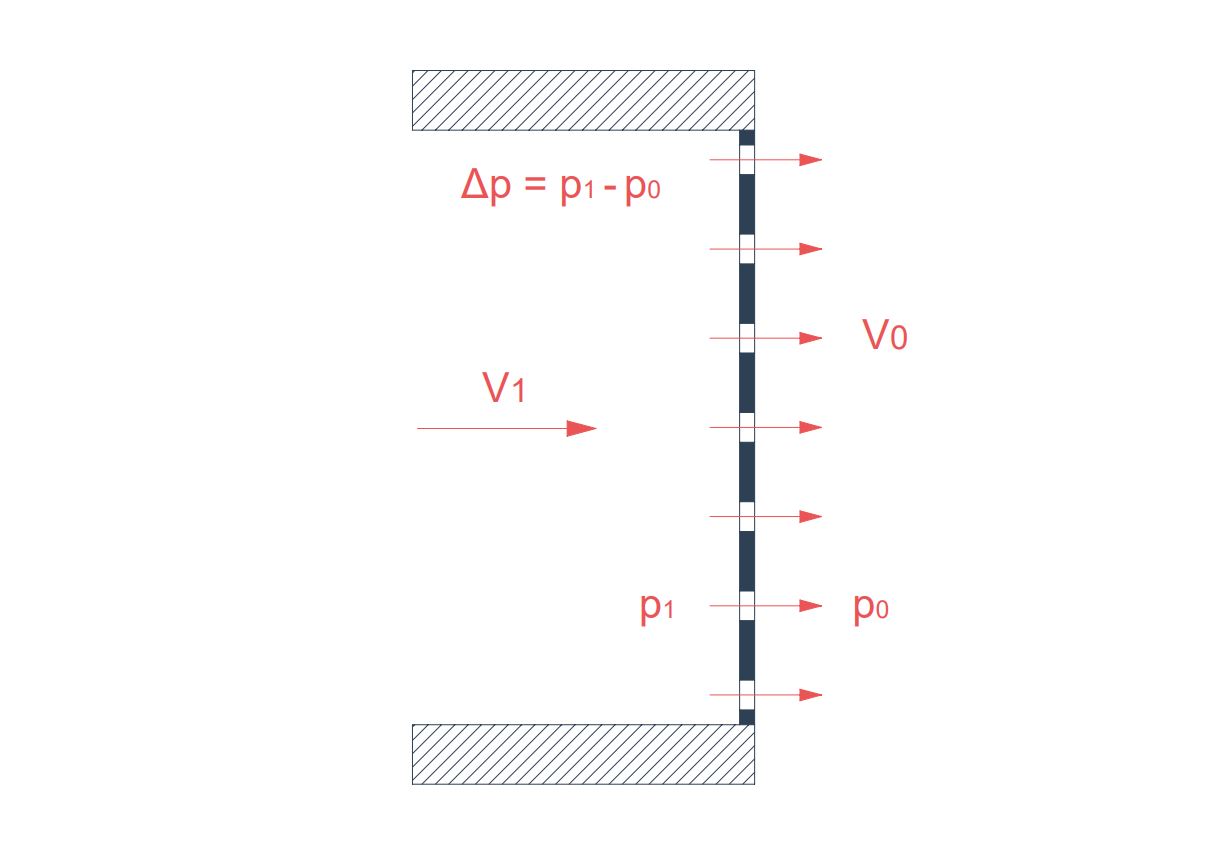
Se define ( \zeta ) (o K) como el coeficiente de pérdida de carga mediante la ecuación fundamental:
\zeta = \Large \frac {\Delta p}{\frac{1}{2} \rho V_1^2}
Siendo:
- \Delta p : caída de presión a través de la placa [Pa].
- V_1 : velocidad de aproximación del aire antes de la placa [m/s].
- \rho : Densidad del aire [kg/m³].
El coeficiente de pérdida de carga ( \zeta ) es función de la relación de área libre o porosidad ( f ) y del número de Reynolds ( Re ). La porosidad ( f ) varía entre 0 (cerrado) y 1 (totalmente abierto).
Para caracterizar el régimen de flujo, calculamos el número de Reynolds basado en el diámetro del orificio:
Re = \Large \frac{V_0 d_h}{\nu}
Donde:
- V_0 : velocidad del fluido dentro del orificio [m/s].
- d_h : diámetro hidráulico del orificio [m].
- \nu : viscosidad cinemática [m²/s].
| Regime | Reynolds | ζ |
|---|---|---|
| Turbulent | Re ≥ 1000 | ζ= ζ (diag.1-2) |
| Transitional | 10 ≤ Re ≤ 1000 | |
| Laminar | Re ≤ 10 | ζ = 30/(f² Re) |
Utilizando la ecuación de continuidad ( f V_0 = V_1 ), podemos expresar el Reynolds en función de la velocidad de aproximación, que es más fácil de medir en conductos:
Re = \Large \frac{V_1 d_h}{f \nu}
Dependiendo del número de Reynolds ( Re ), el flujo se comporta de manera diferente. Esto es crítico para una simulación precisa, ya que el coeficiente \zeta no es constante en todos los regímenes.
Del Papel a la Simulación: El Modelo de Medios Porosos
En software CFD como Ansys Fluent u OpenFOAM, las placas perforadas suelen modelarse como «Medios Porosos» (Porous Media) o «Cell Zones» para ahorrar coste computacional. El software utiliza la Ecuación de Darcy-Forchheimer, que relaciona el gradiente de presión con la velocidad usando dos coeficientes de resistencia distintos:
\large\frac{\Delta p}{L}\normalsize = \underbrace{\frac{\mu}{\alpha} v}_{\text{Viscoso}} + \underbrace{C_2 \frac{1}{2} \rho v^2}_{\text{Inercial}}
También se puede relacionar el coeficiente de pérdida de carga adimensional (o K) con los coeficientes del modelo de medios porosos ( y C_2 ) que piden Ansys Fluent u OpenFOAM.
Donde:
-
K : coeficiente de pérdida de carga (Adimensional).
-
L : espesor de la placa o medio poroso [m].
-
\alpha : permeabilidad [m²].
-
C_2 : coeficiente de resistencia inercial [m⁻¹].
-
\mu : viscosidad dinámica [Pa·s].
-
\rho : densidad del fluido [kg/m³].
-
v : velocidad del fluido [m/s].
- Régimen Laminar (Re < 10): El Término Viscoso (1/α)
A bajas velocidades, el término viscoso domina. La caída de presión es lineal (\Delta p \propto v). En esta zona, \zeta cae rápidamente al aumentar el Reynolds. En Ansys, esto se controla mediante la Viscous Resistance (1/α).
- Régimen Turbulento (Re > 1000): El Término Inercial (C_2)
A altas velocidades, las fuerzas de inercia dominan. La caída de presión se vuelve cuadrática (\Delta p \propto v^2) y \zeta se vuelve constante. En Ansys, esto se controla mediante la Inertial Resistance (C_2).
- La Zona Crítica de Transición (Re ≈ 10 – 1000)
La mayoría de los sistemas industriales de ventilación y filtrado operan en este rango. Aquí, ningún término es despreciable. Las fórmulas estándar suelen fallar porque \zeta es una curva compleja que depende tanto de la viscosidad como de la geometría.
Para simular esto con precisión, en Atreydes Engineering calculamos ambos coeficientes (1/\alpha y C_2) para reconstruir la curva exacta de pérdida de carga de tu fluido y geometría específica.
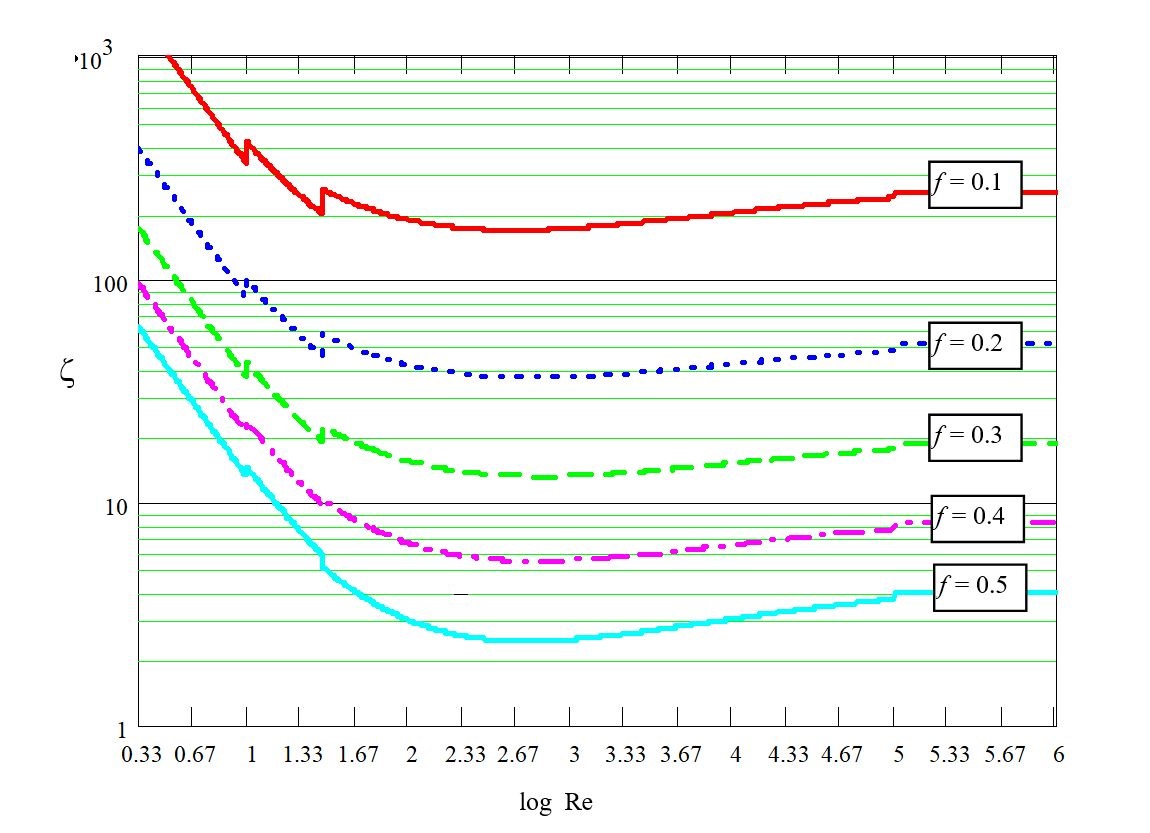
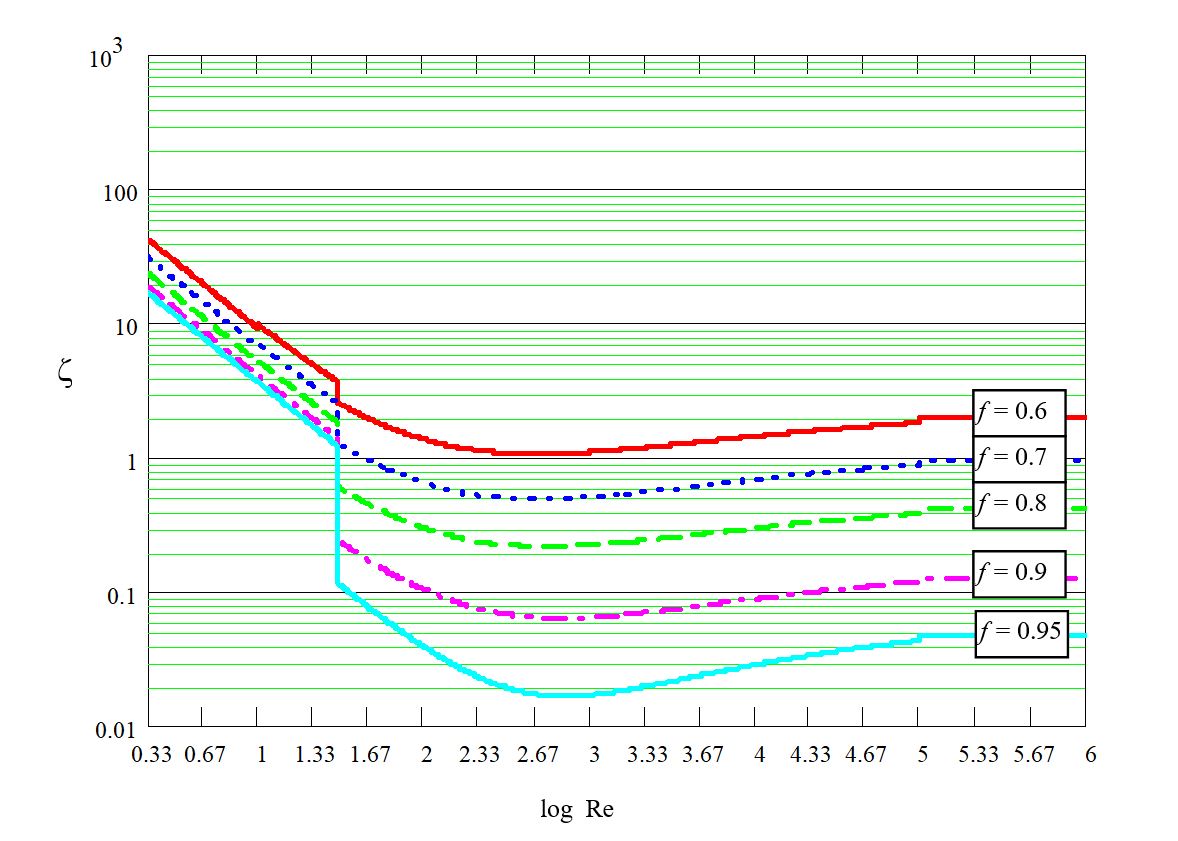
Los siguientes diagramas (escala doble logarítmica) muestran el comportamiento empírico de \zeta utilizado para calibrar estos modelos CFD:
¿Necesitas cálculos precisos de pérdidas de carga?
Deja de confiar en aproximaciones para equipos críticos. Simulamos la geometría exacta de tu placa perforada mediante CFD avanzado para determinar la resistencia hidráulica precisa.

