En los posts de Atreydes Engineering, hemos remarcado la importancia de la definición de un amortiguamiento para seguidores solares (ξ) que permita retrasar, mitigar o eliminar los fenómenos aeroelásticos en el diseño de seguidores solares a un eje.

Aquí, se definirán los amortiguadores físicos necesarios para tal fin de acuerdo con los resultados de las ecuaciones para evitar el galope torsional y del análisis del desprendimiento de vórtices para evitar la resonancia, o al menos, una vibración excesiva que introduzca tensiones elevadas en los componentes del seguidor bajo las velocidades de viento de diseño de la planta.

De acuerdo con estas premisas y con la geometría del seguidor definida en los posts para el cálculo del galope torsional y el análisis de desprendimiento de vórtices, el coeficiente de amortiguamiento necesario para garantizar su estabilidad a lo largo de la vida de la planta tiene un valor aproximado de 0.25.

Dado que la estructura de un seguidor no puede proporcionar por si mismo este amortiguamiento, serán, por lo tanto, amortiguadores lineales los que lo hagan, ya que son componentes baratos y fáciles de instalar.

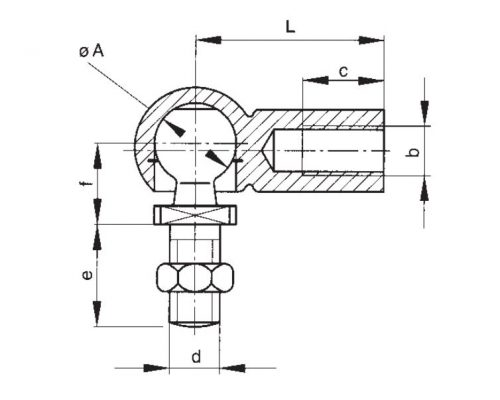
Es importante recordar que un seguidor necesita un amortiguamiento torsional que debe ser proporcionado por amortiguadores lineales. Por este motivo, la posición del amortiguador no es trivial con respecto al eje de giro del seguidor, ya que se tienen que cumplir algunos requisitos geométricos:

El brazo de palanca es un parámetro muy importante porque expresa la cantidad de giro que se produce por cada unidad de avance del amortiguador. A mayor brazo de palanca (d) mejor será el comportamiento del amortiguador con respecto al seguidor, ya que proporcionará una mejor respuesta a su giro con la menor fuerza posible.

Así se puede establecer una relación entre la variación del ángulo que gira el seguidor (Δθ) y la variación de la extensión del amortiguador (Δx):

\Delta \theta \approx \Large \frac{\Delta x}{d}

Siendo d el brazo de palanca.

Derivando la expresión con respecto al tiempo, tenemos que:

\dot \theta \approx \Large \frac{\dot x}{d}

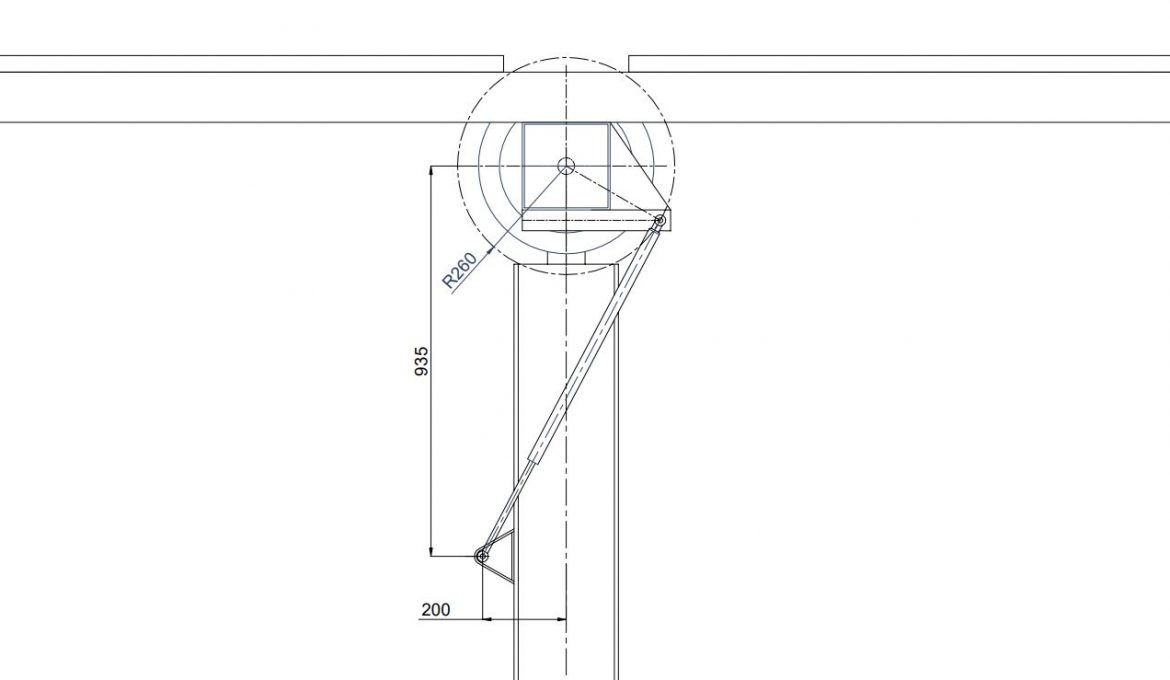
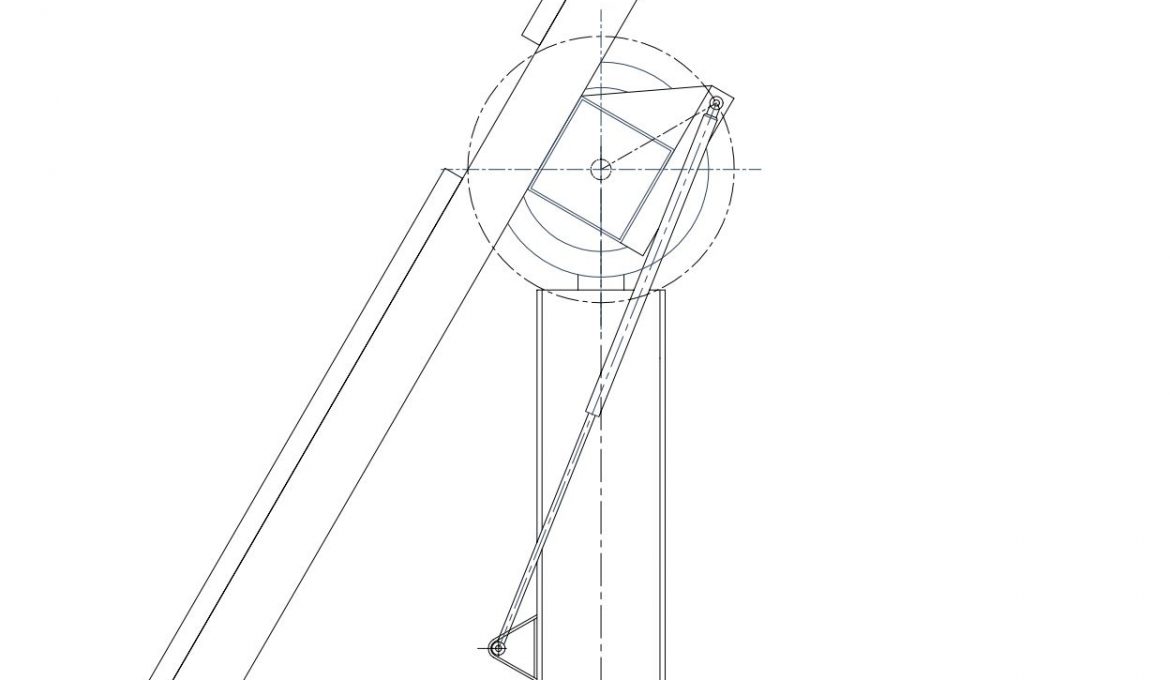
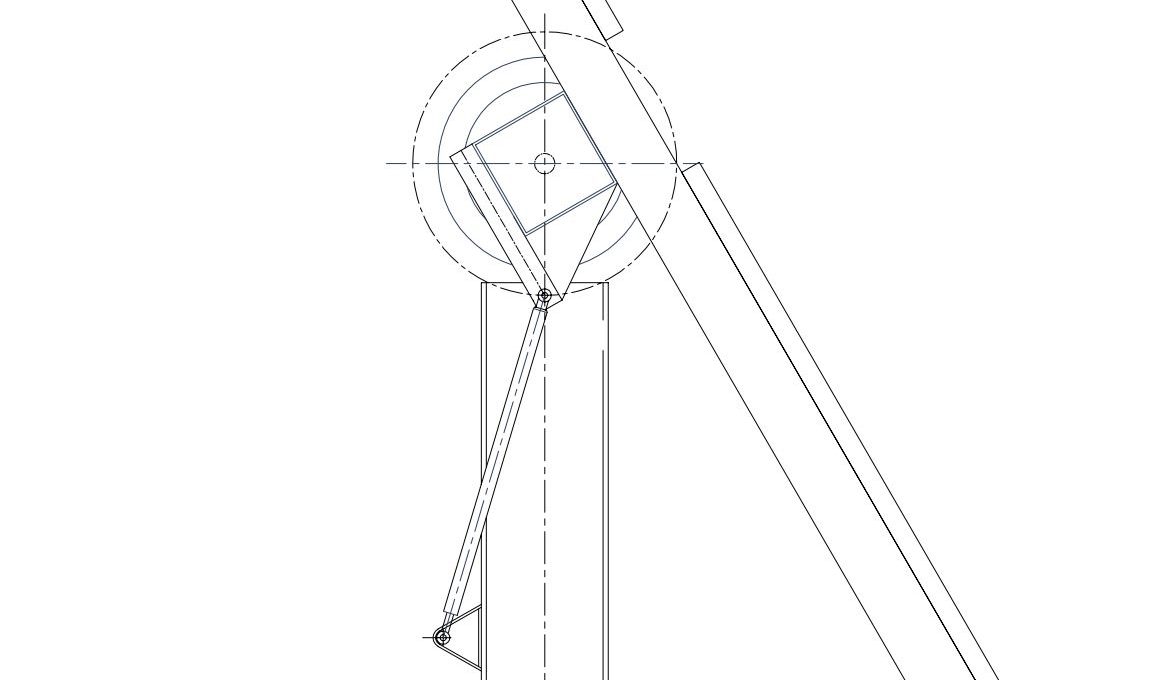
Para la configuración definida en las imágenes anteriores, se expone gráficamente la variación del brazo de palanca con respecto a la inclinación del seguidor.

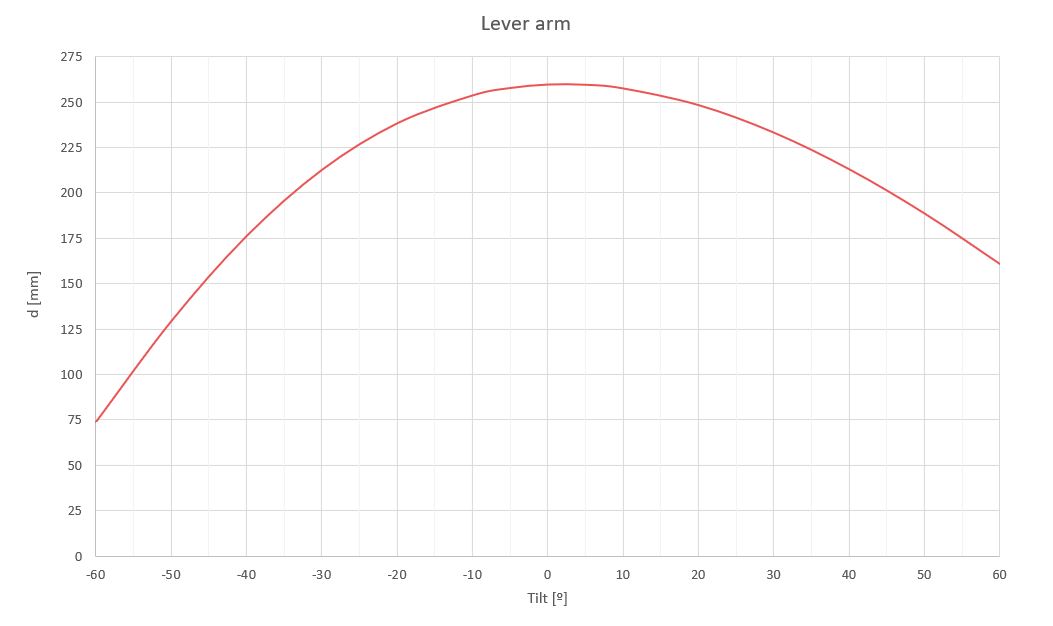
Es necesario matizar que es preferible que el mayor brazo de palanca coincida con la posición de abatimiento del seguidor ya que esta inclinación soportará las cargas y momentos más altos de diseño, correspondientes a las velocidades de viento supervivencia de la planta (Vsurv).

De acuerdo con las ecuaciones definidas en nuestro post Aeroelasticidad solar, el amortiguamiento para seguidores solares ( \hat c_\theta ) necesario para definir nuestros amortiguadores lineales es:

\xi = \Large \frac{\hat c_\theta}{2\hat I \omega_n}

Despejando tenemos que:

\hat c_{\theta} = 2 \xi \hat I \omega_n = 4 \pi \hat I n

Donde:

• \hat c_\theta : amortiguamiento angular tridimensional del sistema.

• \xi : coeficiente de amortiguamiento. 0.25.

• \hat I : inercia tridimensional que interviene en el modo de vibración. 800kgm².

• n : frecuencia natural del sistema. 2.1Hz.

Con estos valores necesitamos un amortiguamiento tridimensional total ( \hat c_\theta ) de 5348 Ns/rad, que se debe repartir linealmente a través de todo el seguidor.

Los amortiguadores lineales necesitan un punto fijo para transmitir la carga que genera la velocidad de rotación del seguidor, de manera que solo es posible amortiguar bajo los pilares del mismo que se utilizarán para transmitir dicha carga, por lo que cada pilar exterior contará con un amortiguador lineal.

Sin contar el pilar central que soporta al mecanismo, se ha tenido en cuenta que cada tubo de torsión de 17.3m se sustenta por 3 pilares exteriores separados una distancia de 5.8m, por lo que cada amortiguador lineal deberá proporcionar un amortiguamiento rotacional de 1783Ns/rad.

c_{\theta i} = \Large \frac{\hat c_\theta}{nº  pillars} \normalsize = 1783Ns/rad

La constante de amortiguación ( c_{\theta i} ) es angular, por lo que habrá que dividir por el brazo de palanca de la posición de defensa ( d_{stow} ) para obtener la constante lineal de nuestros amortiguadores. Se toma como referencia la posición de defensa porque ésta será la posición donde los amortiguadores realicen un mayor trabajo para estabilizar, por un lado, las mayores cargas del seguidor a la velocidad de supervivencia de la planta y evitar, por otro, la aparición del galope torsional.

c_{xi} = \Large \frac{\hat c_{\theta i}}{d_{stow}} \normalsize = 6858Ns/rad

Este parámetro indica que el amortiguador tiene que transmitir una carga de 6858N por cada metro por segundo con que el seguidor empuje o tire de él. También es la causa por la que la amplitud de una vibración armónica en seguidor no sea tan alta y vaya disminuyendo en el tiempo.

Dado que la constante de amortiguamiento es difícil de determinar, los amortiguadores lineales se catalogan por la fuerza que transmiten.

Para nuestros cálculos, las velocidades angulares máximas son un resultado de los análisis CFD. De acuerdo con ellos, esta velocidad angular máxima se encuentra en el caso de posición de defensa a velocidad de supervivencia de la planta.

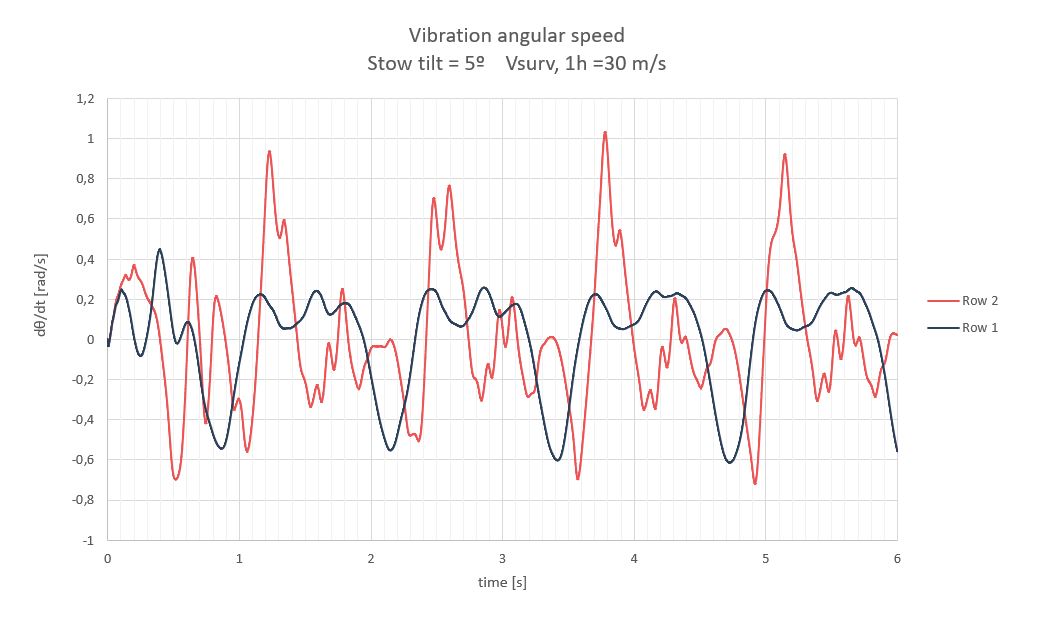
A efectos prácticos podemos considerar una velocidad máxima de ±1rad/s, por lo que la fuerza máxima de tracción como de compresión que debe transmitir el amortiguador es de:

F = c_{xi}  \dot x = c_{\theta i} \Large  \frac{\dot \theta}{d_{stow}} \normalsize = 1783 \Large  \frac{1}{0.26} \normalsize = 6858N

A continuación, se muestran una serie de parámetros a tener en cuenta en el diseño del amortiguamiento para seguidores solares: