
Aeroelasticidad en seguidores solares
Con el auge y estandarización de las plantas fotovoltaicas de seguidores a un eje, la competencia entre fabricantes de dichos seguidores es cada vez más feroz. Para suministrar máquinas y estructuras cada vez más económicas a menudo se recurre a una reducción del material que conforma el seguidor, lo que repercute en un descenso de la rigidez y amortiguamiento del mismo pudiendo aparecer fenómenos de aeroelasticidad en seguidores solares, a menudo, poco predecibles por medio del cálculo clásico.
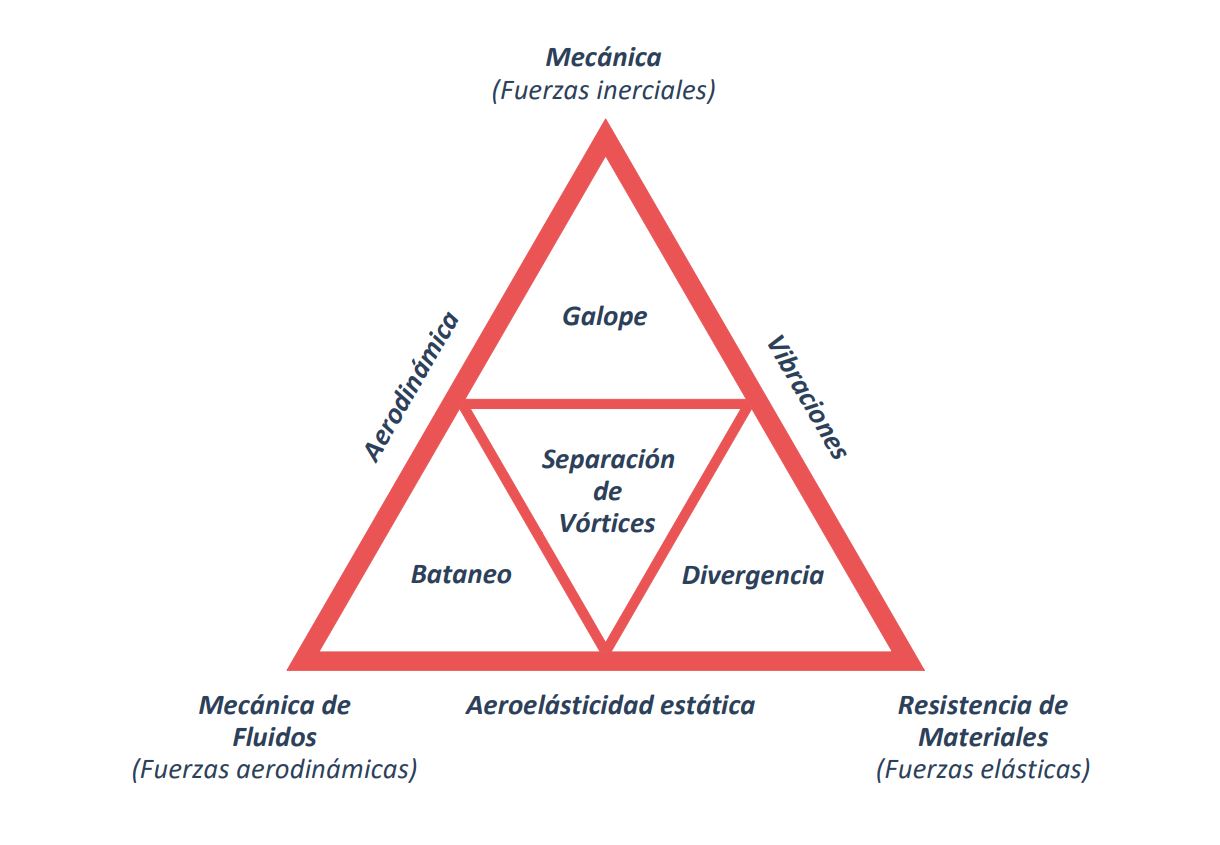
En este post se exponen los parámetros que influyen en los diferentes fenómenos de aeroelasticidad en seguidores solares de un eje, así como las directrices para su análisis en túneles de viento, ya que necesitan de la rigidez y amortiguamiento de la estructura del seguidor para observar el acoplamiento de las fuerzas aerodinámicas a las ecuaciones que gobiernan la respuesta del mismo.
Movimiento oscilatorio
Es muy probable que los fenómenos de aeroelasticidad en seguidores solares de un eje aparezcan asociados al único grado de libertad que poseen, ya que hacen uso de un tubo de torsión muy lago y esbelto para transmitir su movimiento. Así, podemos plantear la ecuación de vibración del seguidor teniendo en cuenta todas las fuerzas que actúan sobre él:
\normalsize I_\theta \ddot \theta + c_\theta \dot \theta + k_\theta \theta = 0
Donde:
- \normalsize I_\theta : inercia polar
- \normalsize c_\theta : amortiguamiento torsional
- \normalsize k_\theta : rigidez torsional
- \normalsize \theta : posición angular de la sección extrema del seguidor
- \normalsize \dot \theta : velocidad angular de sección extrema del seguidor \Large \frac {d\theta}{dt}
- \normalsize \ddot \theta : aceleración angular de la sección extrema del seguidor \Large \frac {d^2\theta}{dt^2}
Si no existen fuerzas aplicadas al seguidor la suma de términos es igual a 0.
A continuación, se definen dos parámetros importes:
- Frecuencia natural angular (\normalsize \omega_n ): es la frecuencia [rad/s] a la que vibra el seguidor cuando entra en resonancia.
\normalsize \omega_n = \sqrt {\Large \frac {k_\theta} {I_\theta}}
- Coeficiente de amortiguamiento (\xi) : indica la relación entre el amortiguamiento del sistema con respecto al amortiguamiento crítico, aquel me marca el inicio de la resonancia.
\normalsize \xi = \Large \frac{c_\theta} {2 I_\theta \omega_n}
Por lo que la ecuación de vibración se expresar como:
\normalsize \ddot \theta + 2 \omega_n \xi \dot \theta + \omega_n^2 \theta = 0
El factor que multiplica a \normalsize \dot \theta se conoce como término de amortiguamiento, mientras que el término de rigidez acompaña a \normalsize \theta .
La solución a la ecuación diferencial de vibración, matemáticamente también llamada solución de la ecuación homogénea es la siguiente:
\normalsize \theta (t) = \exp(-\xi \omega_n t) \left[A \cos(\omega_d t) + B sin(\omega_d t)\right]
Donde A y B son constantes que se definen con condiciones iniciales, siendo ( \normalsize \omega_d ) la frecuencia amortiguada:
\normalsize \omega_d = \omega_n \sqrt{1-\xi^2}
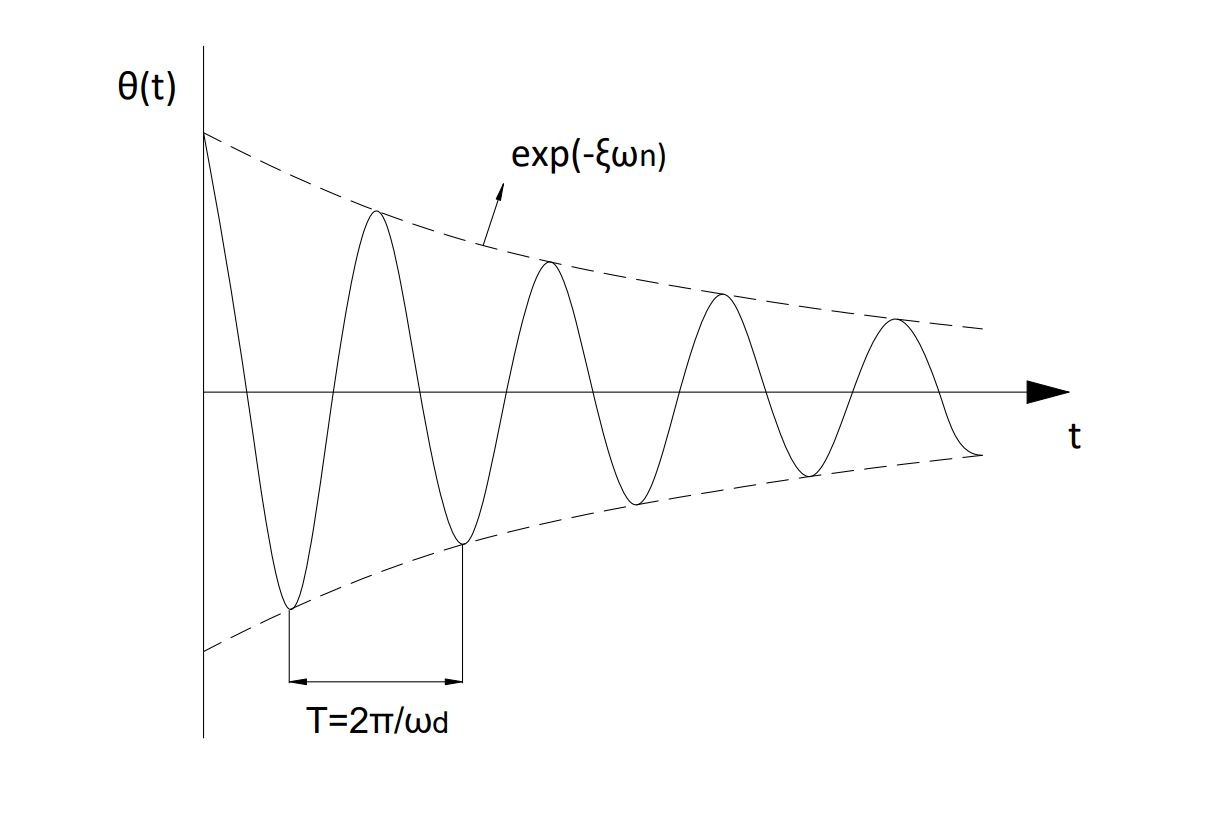
Cuando otras fuerzas externas intervienen en la ecuación otros términos se añaden a esta solución, pero debido a que esta ecuación homogénea representa al sistema puramente mecánico, el seguidor tendrá una parte de su respuesta resonante que pasará inevitablemente por la solución descrita.
El flameo (fluttering) es un fenómeno característico de la aeroelasticidad y fue una de las primeras oscilaciones observadas. Aunque estos tipos de inestabilidades aeroelásticas son propias de las estructuras aeronáuticas, algunas pueden aparecer también en estructuras civiles sobre todo si sus secciones son rectas y alargadas, guardando cierta similitud con los perfiles de las alas de aeronaves, como es el caso de la aeroelasticidad en seguidores solares
Hay que decir que parece existir cierta confusión entre los términos flameo (fluttering) y galope (galloping), sobre todo si en las instabilidades interviene un único grado de libertad. En general, se suele utilizar el calificativo de galope cuando se habla de estructuras no aeronáuticas, excepto si el flameo es clásico, donde están implicadas dos grados de libertad, que ocasionalmente se aplica a ambos tipos de estructuras.
Es importante señalar que el movimiento oscilatorio un cuerpo que genera sustentación, como el movimiento oscilatorio modifica las fuerzas aerodinámicas, si el flujo es potencial o casi potencial, en virtud del teorema de la conservación de la vorticidad, necesariamente han de desprenderse torbellinos que son arrastrados hacia la estela y que interaccionan con la corriente fluida alrededor del cuerpo.
Sin embargo, este tipo de desprendimiento de torbellinos es completamente diferente del asociado a la calle de torbellinos de von Karman, pues en este otro mecanismo los torbellinos se desprenden formando una estela turbillonaria incluso aunque no haya movimiento transversal del cuerpo.
Los fenómenos aeroelásticos que aparecen en una planta de seguidores a un eje son:
Divergencia y Galope Torsional
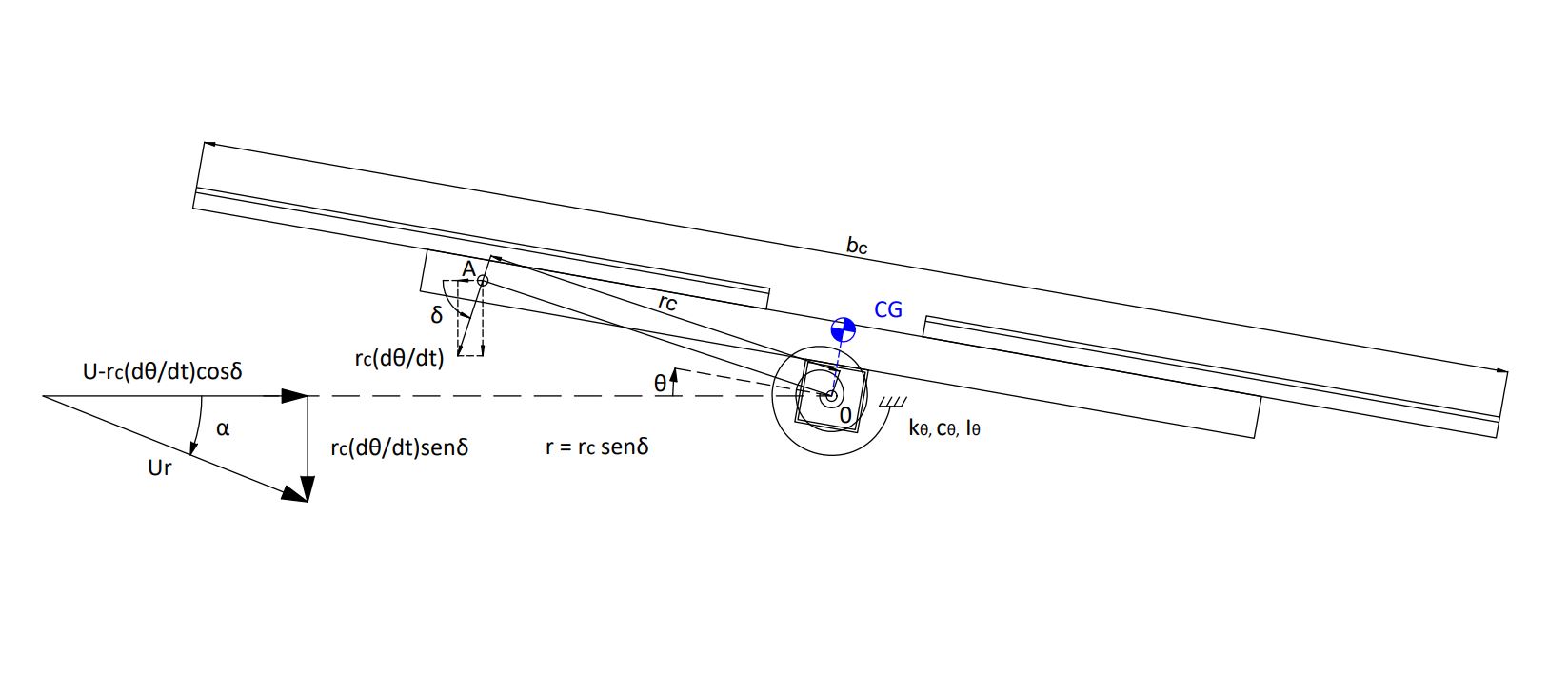
Si simplificamos las fuerzas aerodinámicas del viento en un punto A sobre el seguidor, la ecuación de vibración del mismo queda modificada por el acoplamiento de las fuerzas dinámicas debidas al viento:
\normalsize I_{\theta}\ddot \theta + (2 I_{\theta} \omega_n \xi + \frac{1}{2} \rho U r b_c^2 \frac{\partial c_m}{\partial \alpha}) \dot \theta + (k_{\theta} - \frac{1}{2} \rho U^2 b_c^2 \frac{\partial c_m}{\partial \alpha}) \theta = 0
Observando el término de rígidez, la divergencia torsional se produce cuando existe una velocidad de viento crítica tal ( U_{cr}|_{div} ), que produce un coeficiente \Large \frac{\partial c_m}{\partial \alpha} \normalsize > 0 que anula la rigidez del sistema:
U_{cr}|_{div} \geq \Large \frac {1} {b_c}\sqrt {\frac {2k_{\theta}}{\rho \frac{\partial c_m}{\partial \alpha}}}
Por otro lado, si miramos el término de amortiguamiento, el galope torsional se produce cuando existe una velocidad de viento crítica tal ( U_{cr}|_{gal} ), que produce un coeficiente r\Large \frac{\partial c_m}{\partial \alpha} \normalsize < 0 que anula el amortiguamiento del sistema.
U_{cr}|_{gal} \geq \Large \frac {-4 I_{\theta} \omega_n \xi} {\rho b_c^2 r \frac{\partial c_m}{\partial \alpha}}
Las funciones que expresan el fluttering tienen forma de hipérbolas con los ejes de coordenadas como asíntotas:
U_{cr}|_{div} \large (\frac{\partial c_m}{\partial \alpha})\normalsize^{(\frac {1} {2})} \normalsize \geq \Large \frac {1} {b_c}\sqrt {\frac {2 k_{\theta}}{\rho }} \normalsize = cte_1
U_{cr}|_{gal} \large (\normalsize r \large \frac{\partial c_m}{\partial \alpha}) \normalsize \leq \Large \frac {-4 I_\theta \omega_n \xi} {\rho b_c^2 } \normalsize = cte_2
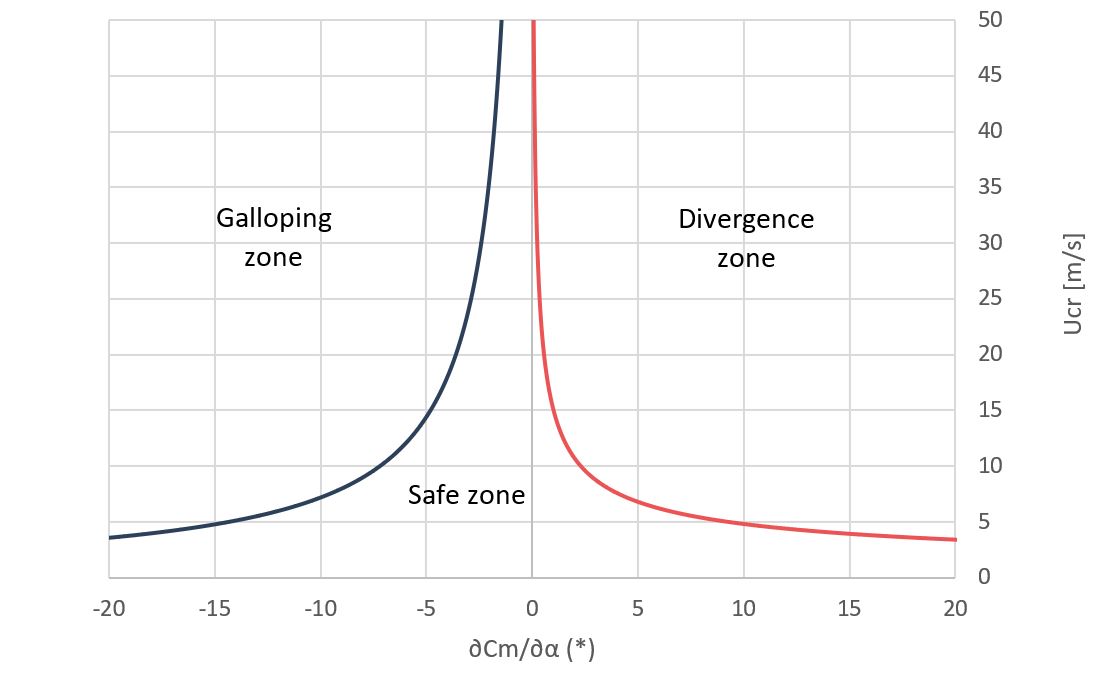
Para retrasar la aparición del fluttering es necesario aumentar el valor absoluto de las constantes, disminuyendo, así, la curvatura de las hipérbolas.
La simplificación de representar el comportamiento dinámico en torsión por la respuesta aeroelástica de un único punto (A) del cuerpo es excesiva y, además, en una configuración real el movimiento oscilatorio alrededor el eje de torsión da lugar al desprendimiento de torbellinos alternados cuyo efecto en las cargas aerodinámicas en el cuerpo no puede ser predicho con un modelo casi estacionario, pero se puede visualizar la dependencia de parámetros para un análisis cualitativo.
Desprendimiento de Vórtices & Bataneo
Las oscilaciones de una estructura inducidas por el desprendimiento de torbellinos son debidas a un efecto de la resonancia de la estructura asociado a la calle de torbellinos que se forma en su estela.
La vibración por bataneo es aquella que se produce por las turbulencias u otras perturbaciones de la corriente no producidas por el obstáculo que las sufre, distinguiéndose dos tipos de bataneo: el generado por la propia turbulencia de la corriente incidente y el debido a las perturbaciones causadas por algún otro cuerpo próximo situado en la corriente arriba del cuerpo en consideración. Este último tipo de bataneo se conoce como bataneo de estela o de interferencia y podríamos encontrarlo en las filas interiores de seguidores que forman una planta solar.
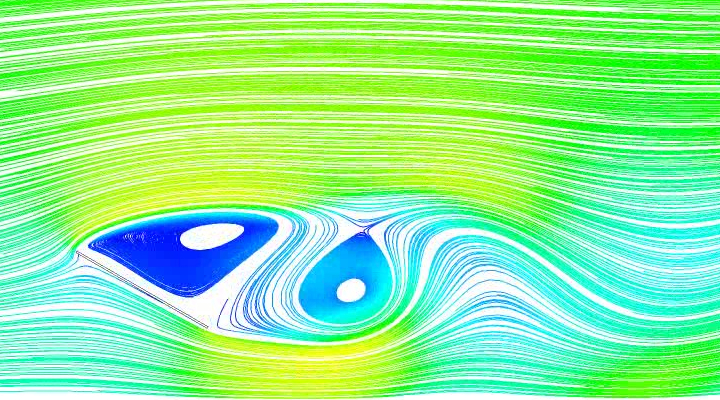
Hay que decir que aunque la vibración inducida por torbellinos y el bataneo de estela pueden ser fenómenos potencialmente dañinos (debido a la fatiga que supone la aplicación de fuerzas alternadas), la formación de una calle de torbellinos da lugar, sin embargo, a una oscilación estable, pues la energía de la excitación tiene un valor infinito para cada frecuencia en particular, que puede ser limitada o eliminada mediante uso de dispositivos amortiguadores, cabiendo también el recurso de alterar la frecuencia de excitación para alejarla de la frecuencia propia de la estructura.
Las diferentes formas de inestabilidad descritas pueden aparecer en un rango amplio de velocidades de viento, por lo que se suelen ensayar en túneles de viento a baja escala, barriendo en velocidad a la espera de la aparición de dichas inestabilidades que se manifestarán por medio de vibraciones de gran amplitud en el eje de torsión del seguidor.
Analizar la aeroelasticidad en seguidores solares requiere comprender que la mecánica del seguidor y las cargas dinámicas de viento se encuentran acopladas, por lo que el túnel de viento debe reproducir las constantes de la ecuación de vibración del seguidor a escala, ya que escaladas se encuentran también las dimensiones del seguidor.
Para ello, se definen 8 parámetros fundamentales:
- \normalsize b_c : longitud característica del seguidor
- \normalsize \rho : densidad del aire
- \normalsize \upsilon : viscosidad cinemática del viento
- \normalsize U : velocidad del viento de ensayo
- \normalsize \theta : ángulo de incidencia
- \normalsize I_\theta : inercia del seguidor
- \normalsize \omega_n : frecuencia natural del seguidor
- \normalsize \xi : coeficiente de amortiguamiento del seguidor
Los parámetros adimensionales entre la escala de la realidad (r) y la escala en el túnel de viento (m) deben cumplir las siguientes expresiones:
\normalsize Re = \Large \left[ \frac {b_c U}{\upsilon} \right]_r \normalsize = \Large \left[ \frac {b_c U}{\upsilon} \right]_m
\Large \left[ \frac {U}{\omega_n b_c} \right]_r \normalsize = \Large \left[ \frac {U}{\omega_n b_c} \right]_m
La longitud característica ( b_c ) en la realidad es mucho mayor que el túnel de viento, por lo que la velocidad debe ser mayor en el túnel de viento que en la realidad para que el número de Reynolds ( Re ) se conserve. Pero en la mayoría de los casos no se cumplirá debido a que los túneles de viento tienen una velocidad máxima que no pueden sobrepasar por diseño.
Dado que se tratan de geometrías angulosas, se puede comprobar que los coeficientes de presión sobre este tipo estructuras no varían con el número de Reynolds, ya que la capa límite se desprende rápidamente, por lo que solo es necesario que, en el túnel de viento, el número de Reynolds sea superior al crítico ( 10^5 ) para asegurar que encuentre dentro del régimen turbulento.
Osborne Reynolds
(Belfast, 1842 – Watchet, 1912)
Ingeniero y físico irlandés que analizó el cambio del régimen laminar al turbulento en el interior de tuberías. Como resultado de estos estudios, en 1883 vería la luz el llamando número de Reynolds (Re), que establece la relación entre las fuerzas inerciales y las viscosas.

También se debe asegurar que el rango de velocidades reducidas ( \Large \frac{U}{\omega_n b_c} ) sea consistente con los valores de las frecuencias propias y la velocidad de diseño del seguidor real. Es importante señalar que muchas veces la rigidez elegida para el seguidor en el túnel no será coincidente en escala con la de la realidad, por lo que se tendrá que escalar la frecuencia con un factor de amplificación o reducción por lo que la velocidad del viento en ensayo se vería también afectada por esta cuestión.
Por último, que un túnel de viento refleje resultados cercanos a la realidad dependerá de que los datos relativos de rigidez y amortiguamiento del seguidor sean los correctos. Estos datos deben ser aproximados en diseño y corroborado por un prototipo, ya que son difíciles de establecer sobre todo los relativos a amortiguamiento, por lo que se suelen ensayar con varios valores de este parámetro.
El resultado suele ser un mapa de valores entre ángulo de inclinación del seguidor ( \theta ) y la velocidad crítica ( U_{cr} ) a la que empieza la inestabilidad para diferentes direcciones de viento.






