Brida Circular Atornillada

En ingeniería, es muy común encontrar una brida circular fijada con tornillos que está sometido a un momento de carga. Es el caso de uniones de tuberías o placa que soportan un rodamiento para movimientos giratorios.

Si se tiene un momento centrado con la brida, dado que los tornillos de la unión se encuentran a diferente distancia del eje de aplicación de dicho momento, cada uno de ellos soportará una fuerza de tracción diferente, por lo que se hace necesario determinar estas cargas para dimensionar la unión atornillada.

Para empezar, los tornillos que más alejados del eje de momentos soportarán una carga máxima (Fmax), que llamaremos simplemente F, mientras que los tornillos que atraviesan el eje del momento tendrán una carga de tracción nula.

Distribución de cargas

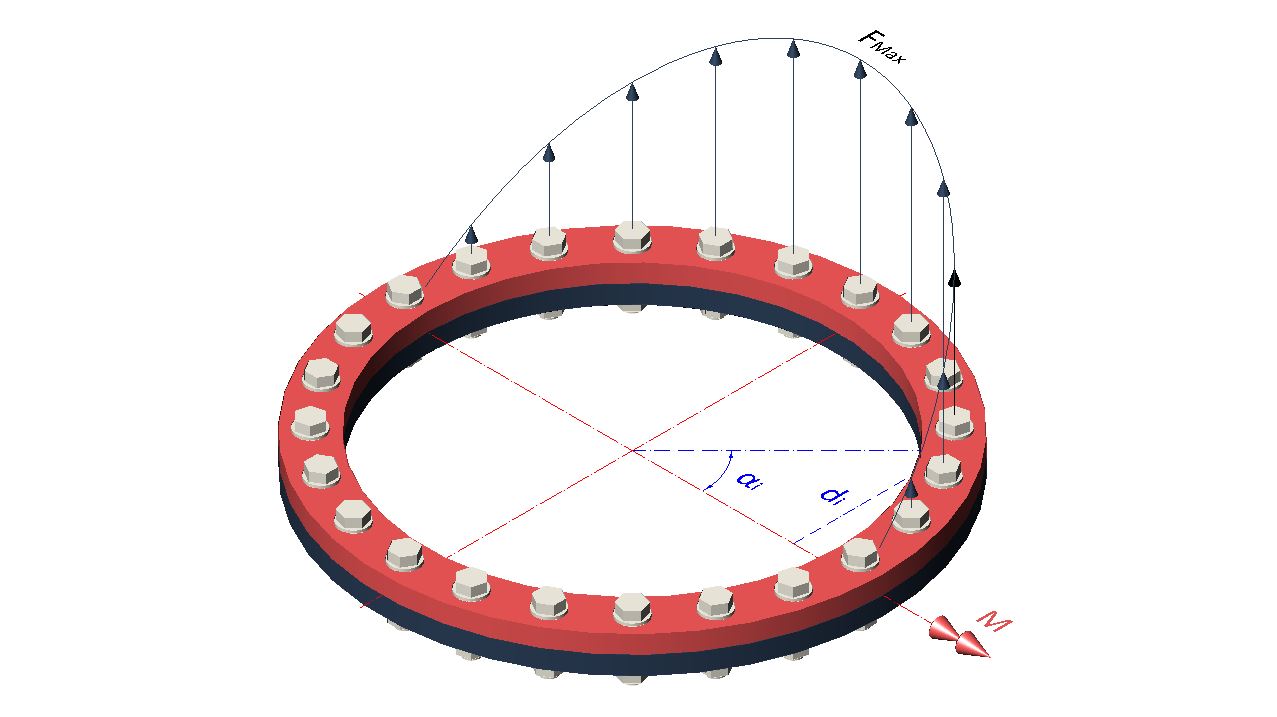
La carga de los demás tornillos entre estas dos posiciones depende de su distancia el eje del memento de acuerdo de forma lineal, si miramos de perfil la brida, pero su contribución al momento depende circularmente de la posición que ocupan en la circunferencia de la brida.

Esquema de distribución de cargas

Así, la distancia de cada tornillo al eje del momento puede calcularse como:

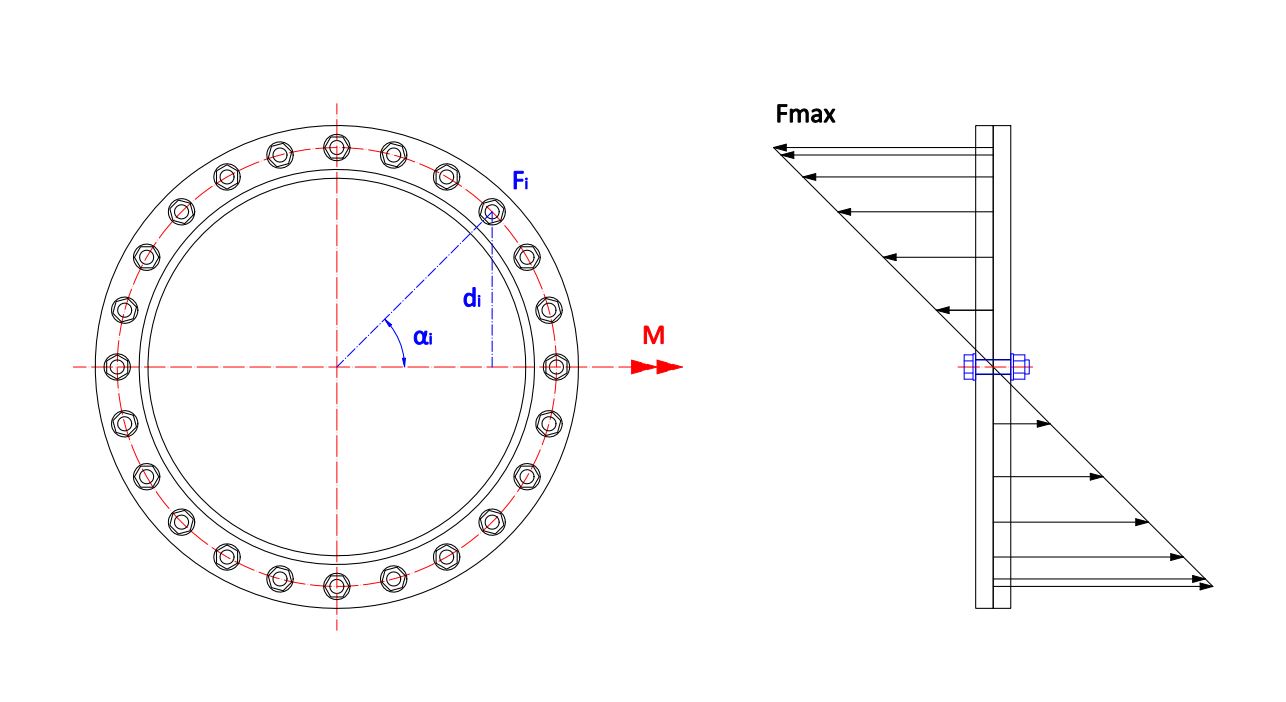
$\normalsize d_i = R sin (\alpha_i)$

Siendo R el radio de la circunferencia de tornillos y α el ángulo con respecto al eje del momento.

$\Large \frac {F}{R} = \frac {F_i}{d_i}$

Donde Fi es la fuerza en cada tornillo, con las demás variables ya definidas. Despejando Fi tenemos que:

Y la fuerza de cada tornillo puede calcularse por triángulos semejantes en el perfil de la brida como:

$\normalsize M = \sum_{i=0}^n F sin (\alpha_i) \cdot R sin (\alpha_i) = F R \sum_{i=0}^n sin^2 (\alpha_i) = \Large \frac {F R n} {2}$

Por lo que la fuerza máxima en el tornillo más alejado al eje del momento será:

$\normalsize F_i = F sin (\alpha_i)$

El momento total sobre la brida (M) será el sumatorio de la fuerza de cada tornillo por su distancia al eje del momento, desde i=0 hasta n

$F = \Large \frac {2 M} {n R}$

Y las fuerzas en cada tornillo, será la fuerza máxima por el seno del ángulo (alfa) que ocupa en la circunferencia.

$\normalsize F_i = F sin (\alpha_i) = \Large \frac {2 M} {n R} \normalsize sin (\alpha_i)$

Hay que señalar que el momento sobre la brida afecta los tornillos a tracción solo a la mitad de ella, ya que la otra mitad, sometida a compresión, intenta juntar ambas placas de dicha brida por lo que los tornillos en esta zona no soportan carga debido al momento.

Más allá de la estática: Aplicación en el mundo real

La fórmula teórica $F = \Large \frac {2 M} {n R}$ proporciona una base sólida para el pre-dimensionamiento. Sin embargo, en maquinaria pesada crítica, confiar solo en cálculos estáticos es un riesgo.

Caso de Éxito: Fatiga en Coronas de Giro (Tecma Drive)
Abordamos un desafío complejo para Tecma Drive S.L.: validar la vida a fatiga de la tornillería en grandes rodamientos de giro (una aplicación masiva de brida circular).

Utilizando el Criterio de Soderberg y Curvas M-Ra personalizadas (Momento vs Carga Axial), analizamos calidades 8.8, 10.9 y 12.9 para garantizar la seguridad bajo cargas cíclicas, previniendo fallos catastróficos en equipos rotativos.

Solicitar Consulta Técnica

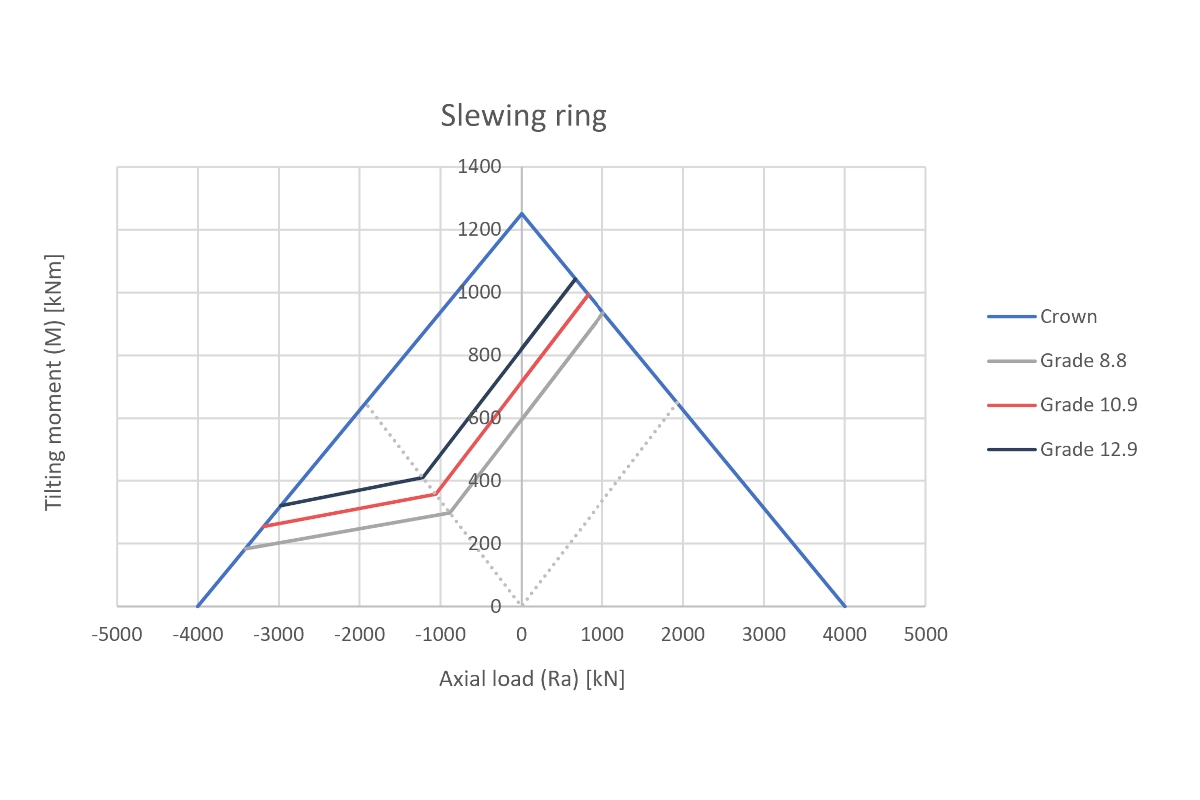
grafica-fatiga-corona-tornilleria-momento-carga-axial-compresion-traccion

Análisis de Fatiga M-Ra desarrollado para Tecma Drive

Desarrollo Matemático

Formulación

\normalsize M = \sum_{i=0}^n F sin (\alpha_i) \cdot R  sin (\alpha_i) = FR \sum_{i=0}^n sin^2 (\alpha_i) =

(1) =  FR \int_0^{2\pi} sin^2 (\alpha) \large \frac {n}{2\pi} \normalsize d\alpha = (2) = \frac {FRn}{2\pi} \int_0^{2\pi} \frac{1}{2}(1-cos (2\alpha)) \normalsize d\alpha =

= \frac {1}{2} \frac {FRn}{2\pi}\{ [\alpha ]_{0}^{\rm 2\pi} - \cancel{[\frac{1}{2} sin(2\alpha)]_{0}^{\rm 2\pi}}\} =\large \frac {FRn}{2}

(1) Integral

\normalsize For  i = 0 \longrightarrow \alpha = 0

\normalsize For  i = n \longrightarrow \alpha = 2\pi

\alpha = \large \frac{2\pi}{n} \normalsize i

i = \large \frac{n}{2\pi} \normalsize \alpha  ;         di = \large \frac{n}{2\pi} \normalsize d\alpha

(2) Trigonometría

\normalsize sin^2 (\alpha) + cos^2 (\alpha) = 1

\normalsize sin^2 (\alpha) = 1 - cos^2 (\alpha)   (A)

\normalsize cos (2\alpha) = cos^2 (\alpha) - sin^2 (\alpha)

\normalsize  cos^2 (\alpha) = cos (2\alpha) - sin^2 (\alpha)   (B)

Sustituyendo B en A:

\normalsize sin^2 (\alpha) = \frac{1}{2} (1 - cos (2\alpha))   (2)

(+34) 605 304 564

Brida Circular Atornillada