Fatiga
grieta de fractura se inicia en una discontinuidad del material donde el esfuerzo cíclico es
máximo.
En esta sección nos centraremos en el cálculo de la fatiga por medio del método esfuerzo-vida, que trata de extrapolar los resultados obtenidos de las probetas de laboratorio a componentes en aplicaciones reales. Se debe tener en cuenta que si bien, es el que tradicionalmente se ha utilizado en ingeniería, no es de los más exactos por lo que los cálculos obtenidos deben considerarse como una aproximación del comportamiento en la realidad. La única manera de saber con exactitud el comportamiento a fatiga de un elemento es ensayarlo ante las cargas cíclicas a las que va a estar sometido. La formulación expuesta en estos apartados hace referencia a materiales ferrosos (aceros) de los que se sabe que tienen una vida infinita a altos números de ciclos ( 10^6 ) para una carga determinada. No pasa así en otros materiales como el aluminio que siempre experimenta una curva descendente por lo que se suele dar un valor de carga a fatiga para 5\cdot10^8 ciclos.
Estimación del límite de fatiga (Se)
De acuerdo con ensayo de probeta de ensayos de diferentes aceros, se puede estimar el límite de fatiga ( S_e' ) a través del límite último a tensión ( S_{ut} ) como:
S_e' = \begin{cases} 0.5 S_{ut} &\text{si } S_{ut} \le 200 kpsi \\ 100 kpsi & \text{si } S_{ut} > 200 kpsi \end{cases}
S_e = k_a \cdot k_b \cdot k_c \cdot k_d \cdot k_e \cdot k_f \cdot S_e'
Factor de superficie (ka)
k_a = a S_{ut}^b
| Surface finish (Acabado superficial) | Factor a | Exponent b |
|---|---|---|
| Ground (Esmerilado) | 1.34 | -0.085 |
| Machined (Mecanizado) | 2.70 | -0.265 |
| Cold-drawn (Laminado en frio) | 2.70 | -0.265 |
| Hot-rolled (Laminado en caliente) | 14.4 | -0.718 |
| As-forged (Forja) | 39.9 | -0.995 |
Factor de tamaño (kb)
k_b = \begin{cases} 0.879d^{-0.107} &\text{para } 0.11 \le d \le 2 in \\ 0.91d^{-0.157} & \text{para } 2 < d \le 10 in \end{cases}
k_b = 1
A_{0.95\sigma} = \Large \frac {\pi}{4} \normalsize [d^21 - (0.95d)^2] = 0.0766d^2 = 0.0766d_e^2
| Sección | A0.95σ | de |
|---|---|---|
| Circular o anular estática de diámetro d | 0.01046d² | 0.370d |
| Rectangular maciza o hueca rotativa de lados b x h | 0.0975hb | 1.128(hb)^(½) |
| Rectangular maciza o hueca estática de lados b x h | 0.05hb | 0.808(hb)^(½) |
Factor de carga (kc)
k_c = \begin{cases} 1 &\text{flexión } \\ 0.85 & \text{axial } \\ 0.59 & \text{torsión } \end{cases}
Factor de temperatura (kd)
k_d = \small 0.975 + 0.432\cdot 10^{-3} T_F - 0.115\cdot 10^{-5} T_F^2 + 0.104\cdot 10^{-8} T_F^3 - 0.595\cdot 10^{-12} T_F^4
Para 70 ≤ T_F ≤ 1000 ºF
Factor de confiabilidad (ke)
| Confiabilidad (%) | ke |
|---|---|
| 50 | 1 |
| 90 | 0.897 |
| 95 | 0.868 |
| 99 | 0.814 |
| 99.9 | 0.753 |
| 99.99 | 0.702 |
| 99.999 | 0.659 |
| 99.9999 | 0.620 |
Factor de efectos varios (kf)
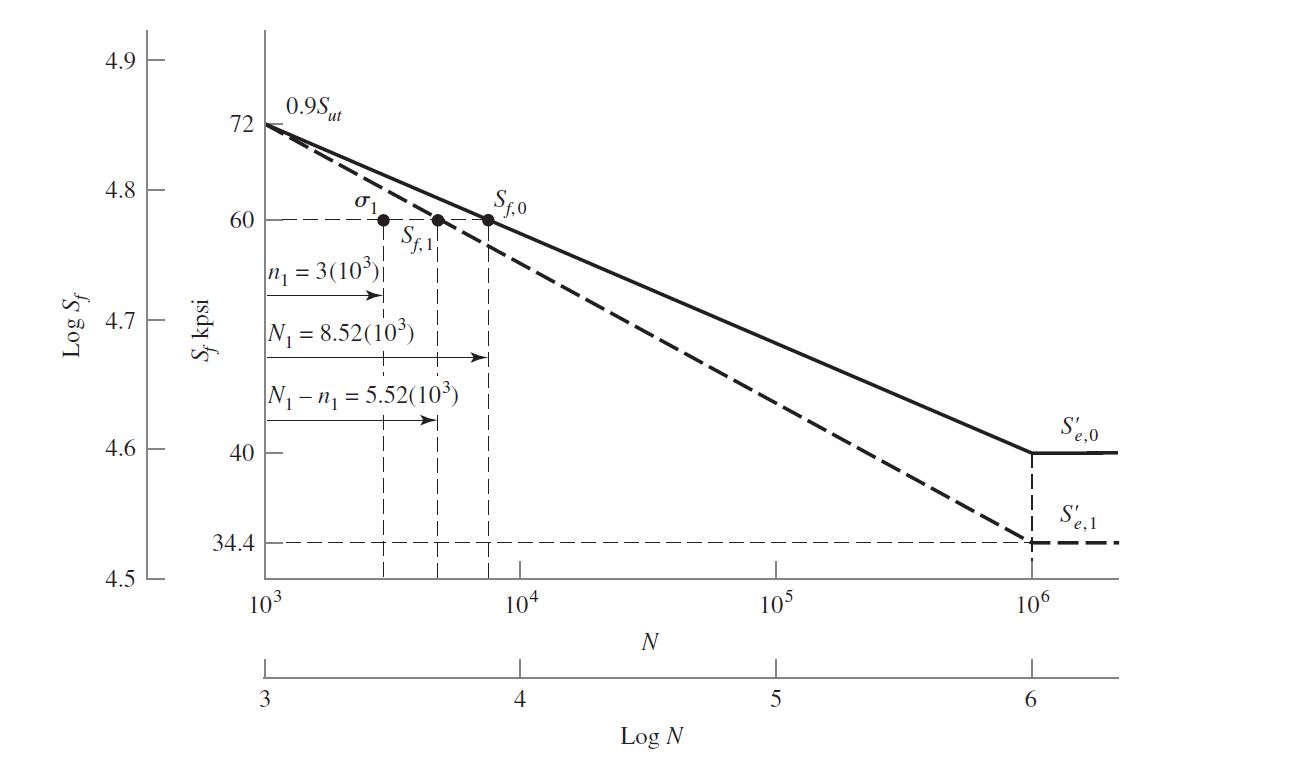
Gráficas S-N
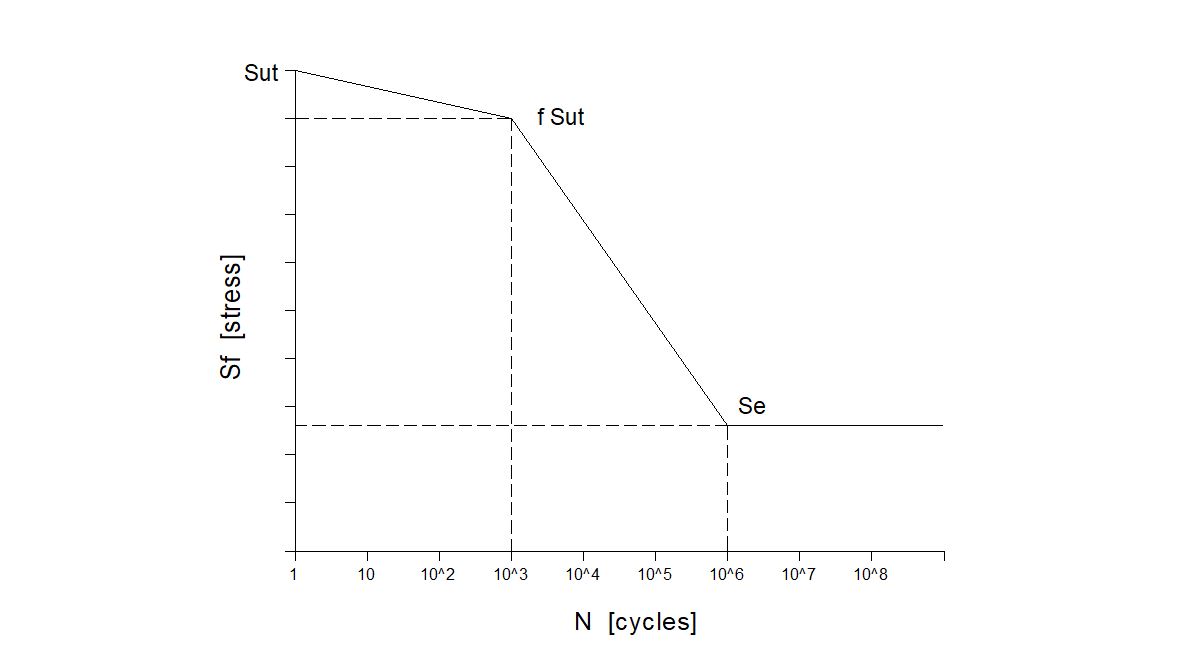
Con la aproximación SAE para aceros con H_B \le 500:
\sigma_F' = S_{ut} + 50 kpsi
Y con b:
c = - \Large \frac {log (\sigma_F' / S_{e}')}{log (2\cdot 10^6)}
Donde S_e' es el límite de fatiga sin modificar.
Concentraciones de esfuerzos (Kf)
K_f = 1+ \Large \frac {K_t - 1}{1 + \frac{\sqrt{a}}{\sqrt{r}}}
Donde \sqrt {a} es la constante de Neuber cuyo valor para esfuerzos flectores y axiales es:
\sqrt{a} = 0.246 - 3.08 \cdot 10^{-3} S_{ut} + 1.51 \cdot 10^{-5} S_{ut}^2 - 2.67 \cdot 10^{-8} S_{ut}^3
Y para torsión:
\sqrt{a} = 0.190 - 2.51 \cdot 10^{-3} S_{ut} + 1.35 \cdot 10^{-5} S_{ut}^2 - 2.67 \cdot 10^{-8} S_{ut}^3
Donde las ecuaciones se aplican al acero, S_{ut} está en kpsi y r es el radio de la muesca en pulgadas (in)
Esfuerzos fluctuantes
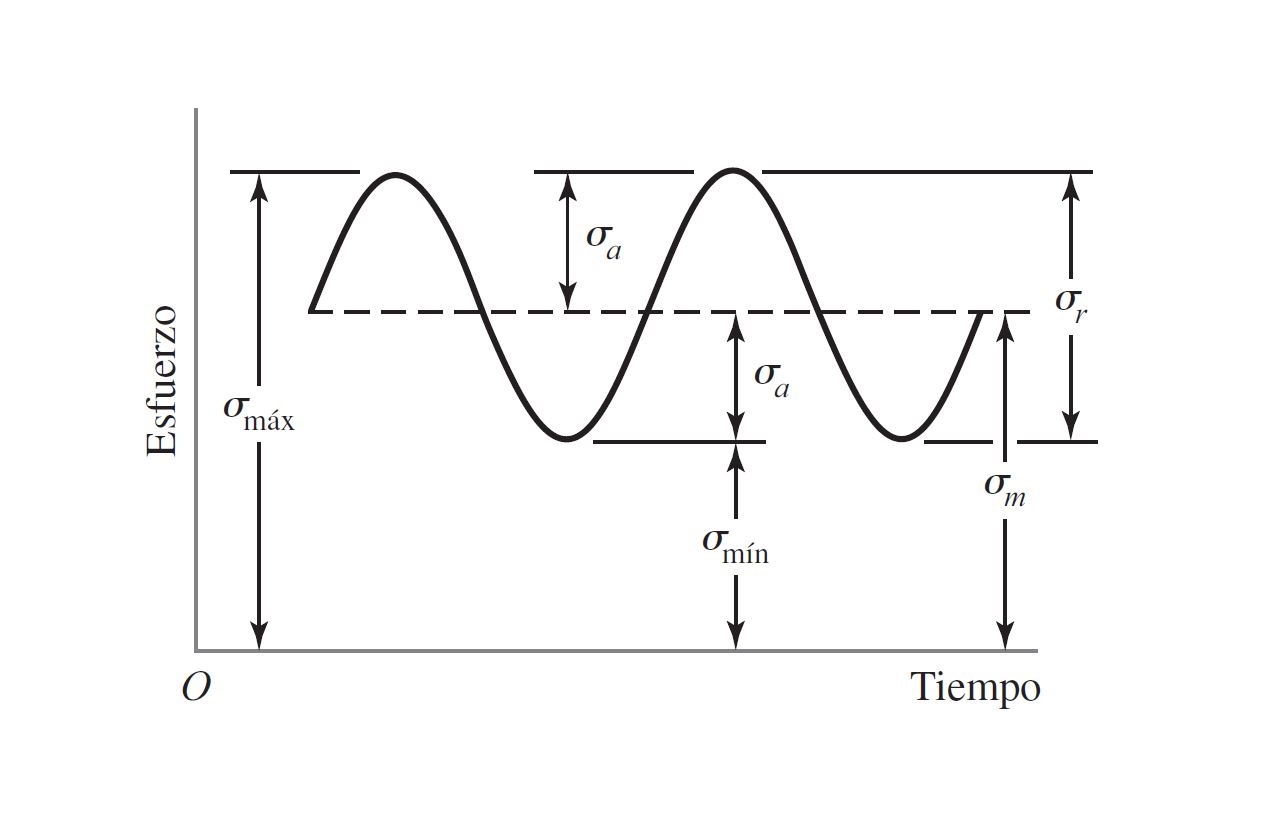
\sigma_{min} = esfuerzo mínimo
\sigma_{max} = esfuerzo máximo
\sigma_{m} = componente de esfuerzo medio
\sigma_{a} = componente de la amplitud
\sigma_{r} = intervalo de esfuerzo
\sigma_m = \Large \frac {\sigma_{max} + \sigma_{min}}{2}
\sigma_a = \Large | \frac {\sigma_{max} - \sigma_{min}}{2}|
Criterios de fallos por fatiga
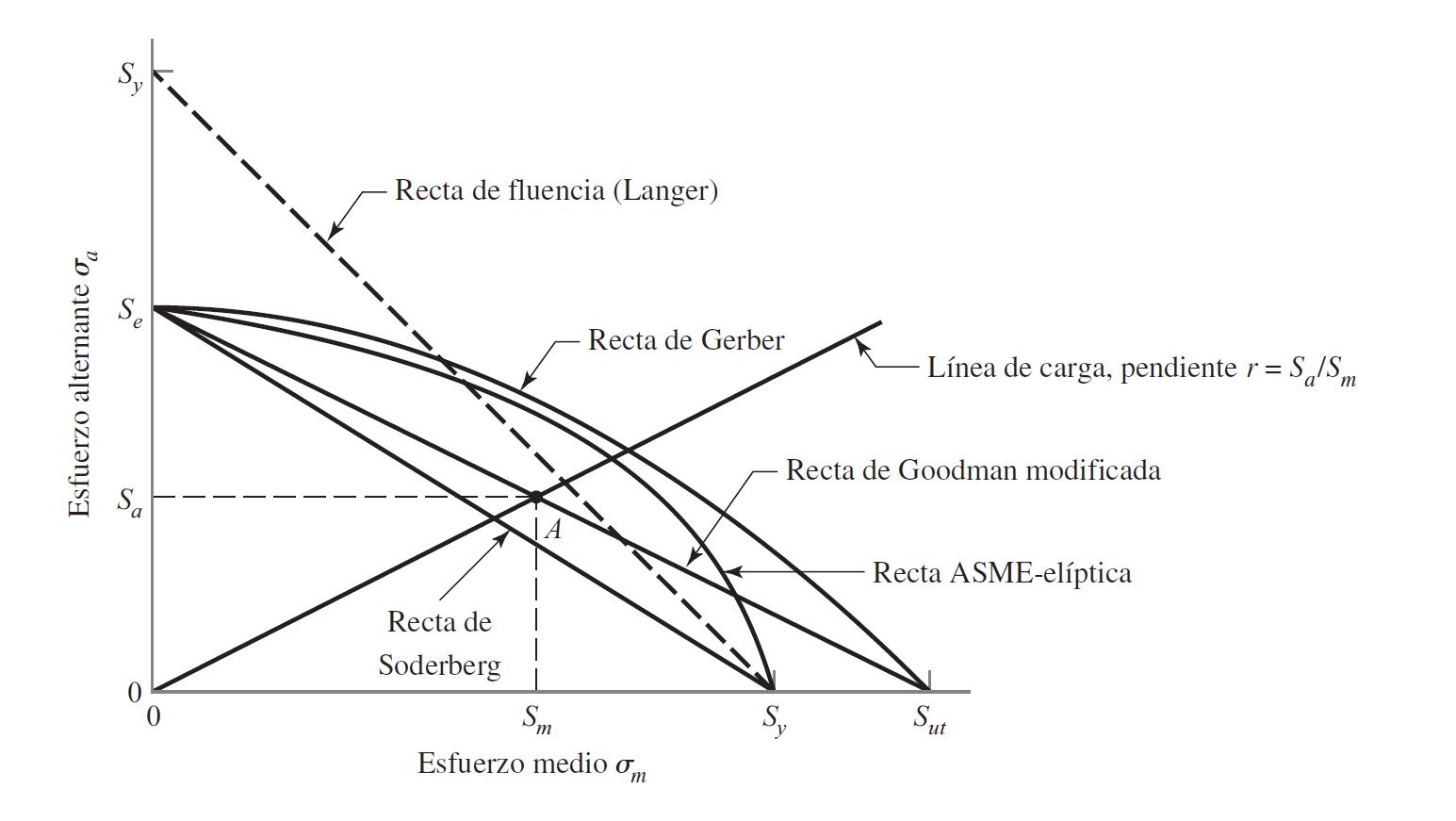
Soderberg
\Large \frac{S_a}{S_e}\normalsize + \Large \frac{S_m}{S_y} \normalsize = 1
Goodman modificado
\Large \frac{S_a}{S_e}\normalsize + \Large \frac{S_m}{S_{ut}} \normalsize = 1
Gerber
\Large \frac{S_a}{S_e}\normalsize + \Large (\frac{S_m}{S_{ut}})\normalsize^2 = 1
ASME-elíptica
\Large (\frac{S_a}{S_e})\normalsize^2 + \Large (\frac{S_m}{S_y})\normalsize^2 = 1
Fluencia estática de Langer
S_a+ S_m = S_y
Los criterios de fallos se utilizan en conjunto con la línea de carga r = S_a/S_m = \sigma_a/\sigma_m
Gerber
S_a = \Large \frac{r^2S_{ut}^2}{2S_e} \left [\normalsize-1+\sqrt{1+ \left(\Large \frac{2S_e}{r S_{ut}} \right)^2} \right]
S_m = \Large \frac{S_a}{r}
n_f = \Large \frac{1}{2} \normalsize \left( \Large \frac{S_{ut}}{S_m} \right)^2 \Large \frac{S_{a}}{S_e} \normalsize \left[ -1+\sqrt{1+ \left(\Large \frac{2 S_m S_e}{S_a S_{ut}}\right)^2}\right]
ASME-elíptica
S_a = \sqrt{\Large \frac{r^2 S_e^2 S_y^2 }{S_e^2 + r^2 S_y^2}}
S_m = \Large \frac{S_a}{r}
n_f = \sqrt{\Large \frac{1}{(S_a / S_e)^2 + (S_m / S_y)^2}}
Esfuerzos fluctuantes y variables

| nº cycle | σmax | σmin | σa | σm | r = σa/σm |
|---|---|---|---|---|---|
| 1 | 80 | -60 | 70 | 10 | 7 |
| 2 | 60 | 40 | 10 | 50 | 0.2 |
| 3 | -20 | -40 | 10 | -30 | -0.333 |
D = \sum_{i=1}^n N_{eq} \left(\Large \frac{1}{n_i} \right)
Combinaciones de carga
Cuando se tienen esfuerzos axiales, flectores y torsores, se calcula la tensión de Von Mises para \sigma_{m}' y \sigma_{a}' como:
\sigma_m' = \sqrt{ \left[ (K_f)_{fl} (\sigma_m)_{fl} + (K_f)_{ax} (\sigma_m)_{ax} \right]^2 +3 \left[ (K_f)_{tor} (\tau_m)_{tor} \right]^2 }
\sigma_a' = \sqrt{ \left[ (K_f)_{fl} (\sigma_a)_{fl} + (K_f)_{ax} (\sigma_a)_{ax} \right]^2 +3 \left[ (K_f)_{tor} (\tau_a)_{tor} \right]^2 }
Una vez calculadas las tensión de Von Mises \sigma_{m}' y \sigma_{a}' , se pueden introducir en los criterios de fatiga ya definidos:
Daño acumulado