Proyectos
Quiénes Somos
Más de 10 años de experiencia en ingeniería, aplicando sinergia de varias áreas de la técnica junto con nuevas tecnologías para garantizar el éxito de nuestros clientes.
Engranajes
En este apartado se definirá la geometría necesaria para conseguir el movimiento entre engranajes rectos de ejes paralelos. No entraremos en el cálculo ya que depende de consideraciones que llevarían mucha literatura como la flexión del diente, durabilidad de la superficie o la fatiga del engranaje.
Geometría
En el diseño de engranajes encontramos 3+1 parámetros fundamentales, de los que dependen los demás parámetros de diseño: el número de dientes del engranaje (z), el diámetro primitivo o de paso (d), que es la circunferencia equivalente al contacto, por la cual el engranaje rueda sin deslizar y el módulo (m) que establece un índice de tamaño del diente en unidades del Sistema Internacional (SI) y que suele estar tabulado en milímetros.
| Módulo | |
|---|---|
| Preferidos | 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50 |
| Siguiente elección | 1.125, 1.375, 1.75, 2.25, 3.5, 4.5, 5.5, 7, 9, 11, 14, 18, 22, 28, 36, 45 |
La relación de estos tres parámetros proporciona la ecuación fundamental de los engranajes y define la geometría de engranaje.
\large d = m \cdot z
El cuarto parámetro es el ángulo de presión (φ) que equivale al ángulo entre la dirección de la fuerza de contacto y la dirección de la velocidad en el engranaje conducido. En construcción de engranajes modernos se viene adoptando el valor de 20º, aunque para aplicaciones especiales también se usa el valor de 14.5º.
Parámetros
Paso circular (p) es la distancia medida sobre la circunferencia primitiva entre puntos homólogos de dos dientes consecutivos. El paso es igual a la suma del grueso del diente y al hueco entre dientes consecutivos.
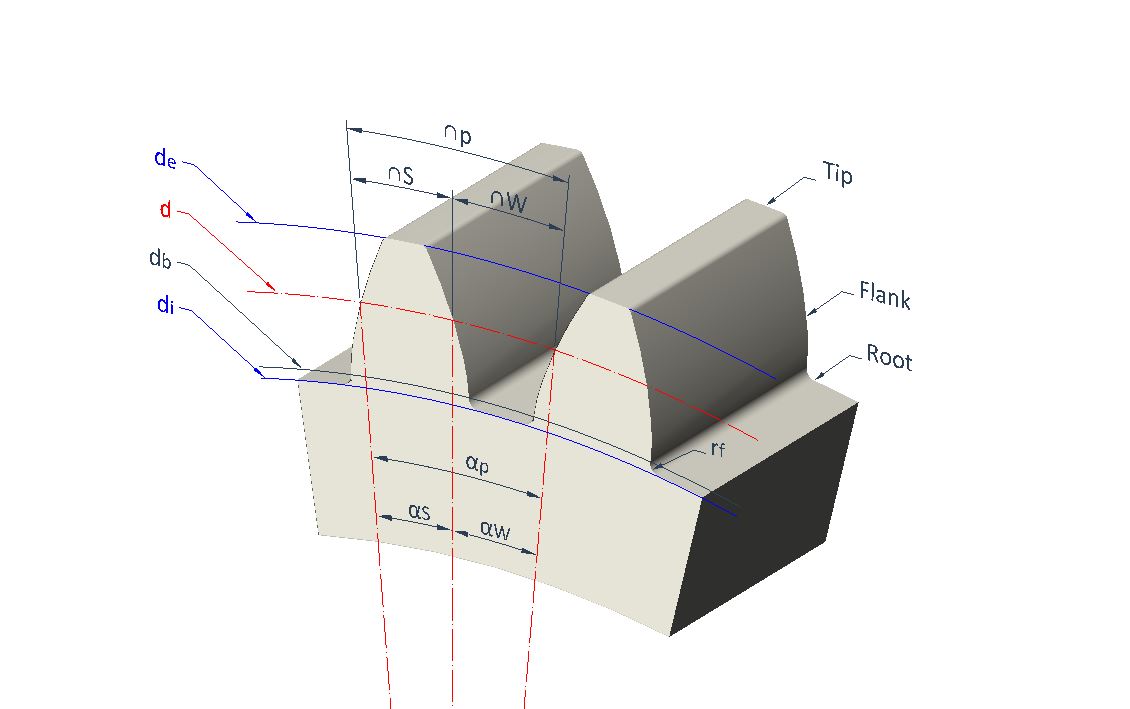
\normalsize p = \Large \frac{\pi d}{z}
Grueso del diente (S): espesor del diente medido sobre el diámetro primitivo.
\normalsize S = p \Large \frac {19}{40}
Hueco del diente: (W): espacio entre diente y diente medido sobre el diámetro primitivo.
\normalsize W = p \Large \frac {21}{40}
Ángulo del paso circular (αp): es ángulo que abarca el paso circular con respecto al centro del engranaje
\normalsize \alpha_p (º) = \Large \frac{2 p}{d} \frac{180}{\pi}
Ángulo del grueso del diente (αS): ángulo que abarca el grueso del diente con respecto al centro del engranaje.
\normalsize \alpha_S (º) = \Large \frac{2 S}{d} \frac{180}{\pi}
Ángulo del hueco del diente (αW): ángulo que abarca el hueco del diente con respecto al centro del engranaje.
\normalsize \alpha_W (º) = \Large \frac{2 W}{d} \frac{180}{\pi}
Diámetro de base (db): diámetro en el que empieza la involuta del flanco del diente.
\normalsize d_b = d cos(\phi)
Diámetro exterior (de): diámetro donde se encuentra la cresta del diente.
\normalsize d_e = d +2m
Diámetro interior (di): diámetro donde se encuentra la raíz del diente.
\normalsize d_i = d -2.5m
Radio de la raíz (rf): radio entre el diente y el diámetro interior.
\normalsize r_f \approx 0.25m
Longitud del diente (l): distancia desde la raíz hasta la cresta del diente.
\normalsize l = \frac {1}{2}(d_e-d_i)
Condición de Engrane
"Dos ruedas dentadas engranan si tienen el mismo módulo."
\large m_1 = m_2
Relación de Transmisión
Matemáticamente, la relación de transmisión puede ser expresada de múltiples maneras, según las siguientes expresiones:
r_t = \Large \frac {\omega_2}{\omega_1} \normalsize = \Large \frac {d_1}{d_2} \normalsize = \Large \frac {z_1}{z_2}
Siendo ω la velocidad angular de cada engranaje, con d y z ya definidos como el diámetro primitivo y número de dientes respectivamente.
Relación de contacto
La relación de contacto (ε), es un parámetro que mide el promedio de dientes que están siempre en contacto. Como norma general, se tratará que ε sea mayor que 1,2. Con ello se garantizará una mayor capacidad del engranaje de transmitir cargas más elevada, proporcionará una mayor rigidez a la transmisión, a la vez que se conseguirá un funcionamiento más uniforme y menos ruidoso.
\varepsilon = \Large \frac {L \tiny AB}{p cos (\phi)} \normalsize> 1.2
La geometría de los parámetros se expone a continuación.
Relación de contacto
La línea de contacto (LAB) se puede calcular como la distancia del punto A al punto B, d(A,B).
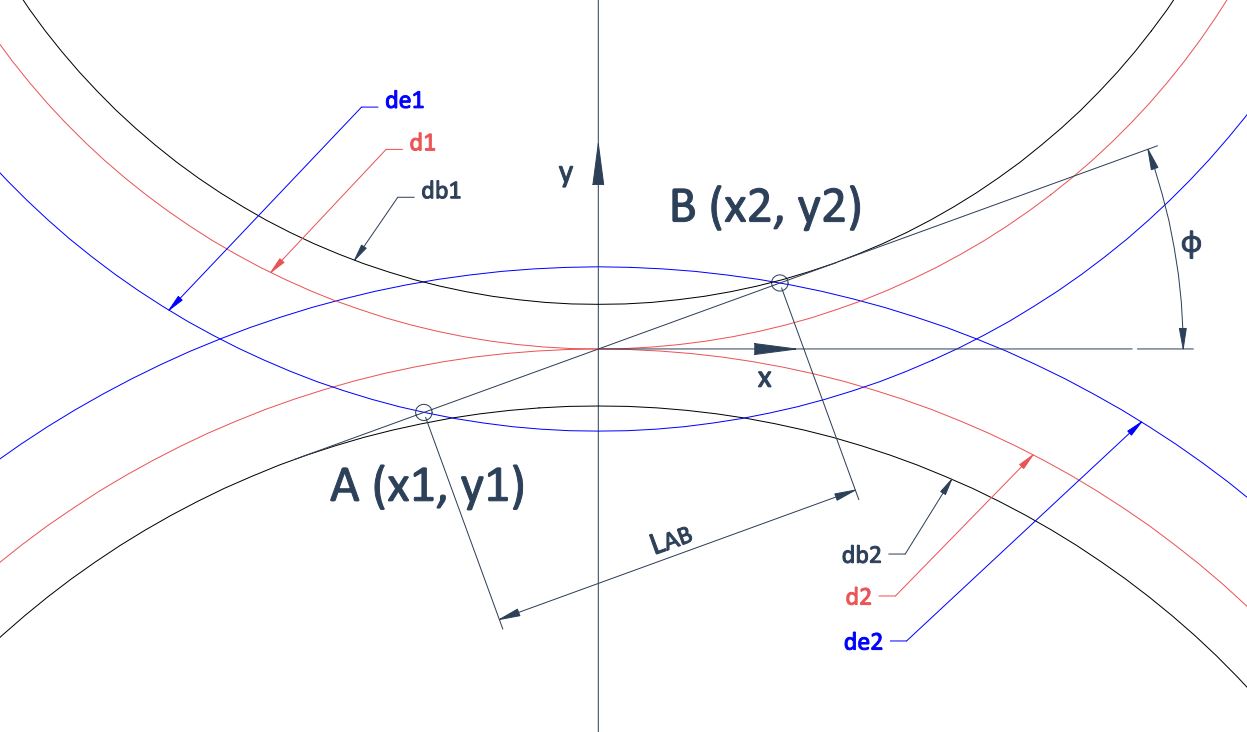
L \tiny AB \normalsize = d(A,B) = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}
Los puntos A(x1, y1) y B(x2, y2) pueden calcularse como la intersección de la línea de contacto (LAB) con las circunferencias exteriores de cada engranaje.
x_1 = \Large \frac{db_1 tan(\phi) - \sqrt{ (1+tan^2(\phi)) (db_1+2m)^2-db_1^2}}{2(1+tan^2(\phi))}
y_1 = tan(\phi) x_1
x_2 = \Large \frac{- db_2 tan(\phi) + \sqrt{ (1+tan^2(\phi)) (db_2+2m)^2-db_2^2}}{2(1+tan^2(\phi))}
y_2 = tan(\phi) x_2
Interferencia
La interferencia ocurre cuando la punta del diente impulsado hace contacto con el flanco del diente impulsor. En este caso el flanco del diente impulsor primero hace contacto con el diente impulsado antes de que la parte involuta del diente impulsor entre en acción. En otras palabras, el contacto ocurre debajo del círculo base del engrane, en la parte no involuta del flanco. El efecto real es que la punta o cara involuta del engrane impulsado tiende a penetrar en el flanco no involuta del impulsor.
Cuando se producen los dientes de engranes mediante un proceso de generación, la interferencia se elimina de manera automática porque la herramienta de corte remueve la parte interferente del flanco. Este efecto se denomina rebaje, pero si éste es muy pronunciado, el diente rebajado se debilita considerablemente. De esta forma, el efecto de la eliminación de la interferencia mediante un proceso de generación sólo sustituye el problema original por otro.
El menor número de dientes en un piñón y engrane rectos, con relación de engrane uno a uno, que pueden existir sin interferencia es Zp1. Este número de dientes de engranes rectos está dado por:
Z_{P1} = \Large \frac{2(k)}{3sin^2(\phi)} \normalsize (1+\sqrt{1+3sin^2(\phi)}) = 12.3 = 13 dientes
Donde k es igual a 1 para dientes de profundidad completa y 0.8 para dientes cortos.
Si la relación de engrane entre el par de engranajes es mayor que 1 igual a n, el piñón más pequeño que puede engranar sin interferencias será:
Z_{Pn} = \Large \frac{2(k)}{(1+2n) sin^2(\phi)} \normalsize (n+\sqrt{n^2+(1+2n) sin^2(\phi)})
El mayor engrane (Zge) para un piñón con numero de dientes especificado (Zpe) que está libre de interferencia es:
Z_{ge} = \Large \frac{Z_{pe}^2 sin^2(\phi)-4k^2}{4k-2Z_{pe}sin^2(\phi)}
| n | Zpn | Zgn |
|---|---|---|
| 1 | 13 | 13 |
| 2 | 15 | 30 |
| 3 | 15 | 45 |
| 4 | 16 | 64 |
| 6 | 16 | 96 |
| 7 | 17 | 119 |
| 77 | 17 | 1309 |
| 78 | 18 | 1404 |
| 90 | 18 | 1620 |
| 100 | 18 | 1800 |
| Zpe | Zge |
|---|---|
| 10 | 4 |
| 11 | 7 |
| 12 | 10 |
| 13 | 16 |
| 14 | 26 |
| 15 | 45 |
| 16 | 101 |
| 17 | 1309 |
| 18 | No limit |
El menor piñón recto que funcionará con una cremallera sin interferencia se determina mediante:
Z_{Pr} = \Large \frac{2(k)}{sin^2(\phi)} \normalsize = 17.1 = 18 dientes
Como las herramientas de formado de engranes implica un contacto con una cremallera, y el proceso de generación por fresa madre de un engrane es semejante, el número mínimo de dientes para evitar interferencia, a fin de evitar rebaje mediante el proceso de fresado, resulta igual al valor de ZPr. La importancia del problema de los dientes que se debilitaron mediante rebaje no se puede menospreciar.
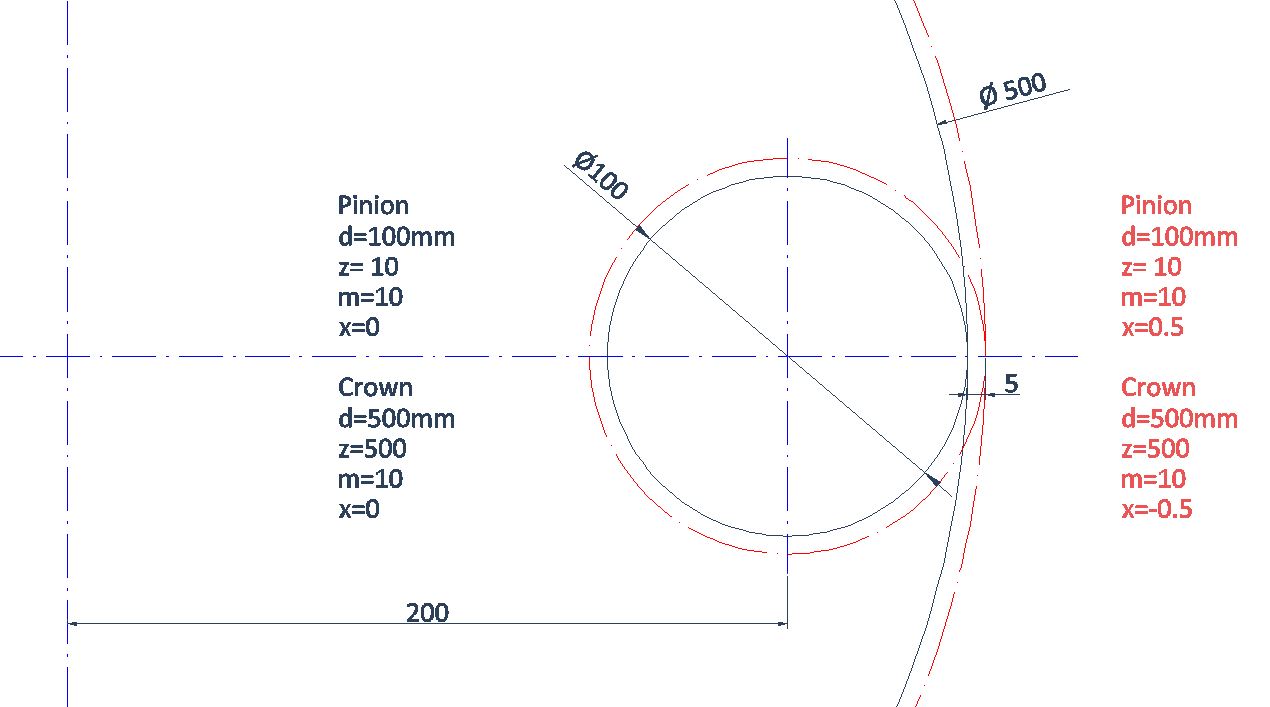
Engranajes modificados
Para evitar este rebaje en la raíz del diente en engranajes con interferencias, se suele modificar el dentado a través de un parámetro llamado modificación (x), cuyo signo es positivo para una engranajes exteriores y negativo para engranajes interiores. Con esto se consigue aumentar la raíz del diente, evitando el rebaje.
Un signo positivo de x indica un retroceso de la herramienta que mecaniza el engranaje mientras que un signo negativo indica un avance para crear el engranaje.
Debido a que esta operación consigue dientes mucho más afilados un segundo parámetro llamado truncamiento (k) los recorta en un diámetro inferior al diámetro exterior. El valor de k siempre es negativo.
Una vez que entran en juego la modificación (x) y el truncamiento (k), la geometría del engranaje se modifica de la siguiente forma:
Comparación entre engranaje ordinario y modificado [m=10, z=10, x=0.5]
Engranajes exteriores (x>0)
S' = S +2 m x tan (\phi)
W' = W +2 m x tan (\phi)
d_e' = d_e +2 m x + 2 m k
d_i' = d_i +2 m x
Engranajes interiores (x<0)
S' = S - 2 m x tan (\phi)
W' = W - 2 m x tan (\phi)
d_e' = d_e - 2 m x - 2 m k
d_i' = d_i - 2 m x
Aunque estos engranajes siguen manteniendo su diámetro primitivo (d) para cumplir con la ecuación fundamental de los engranajes, a efectos prácticos es como si lo modificaran a (d') para engranar con otros:
d' = d + 2 m x para engranajes exteriores
d' = d - 2 m x para engranajes interiores
Diámetros primitivos modificados
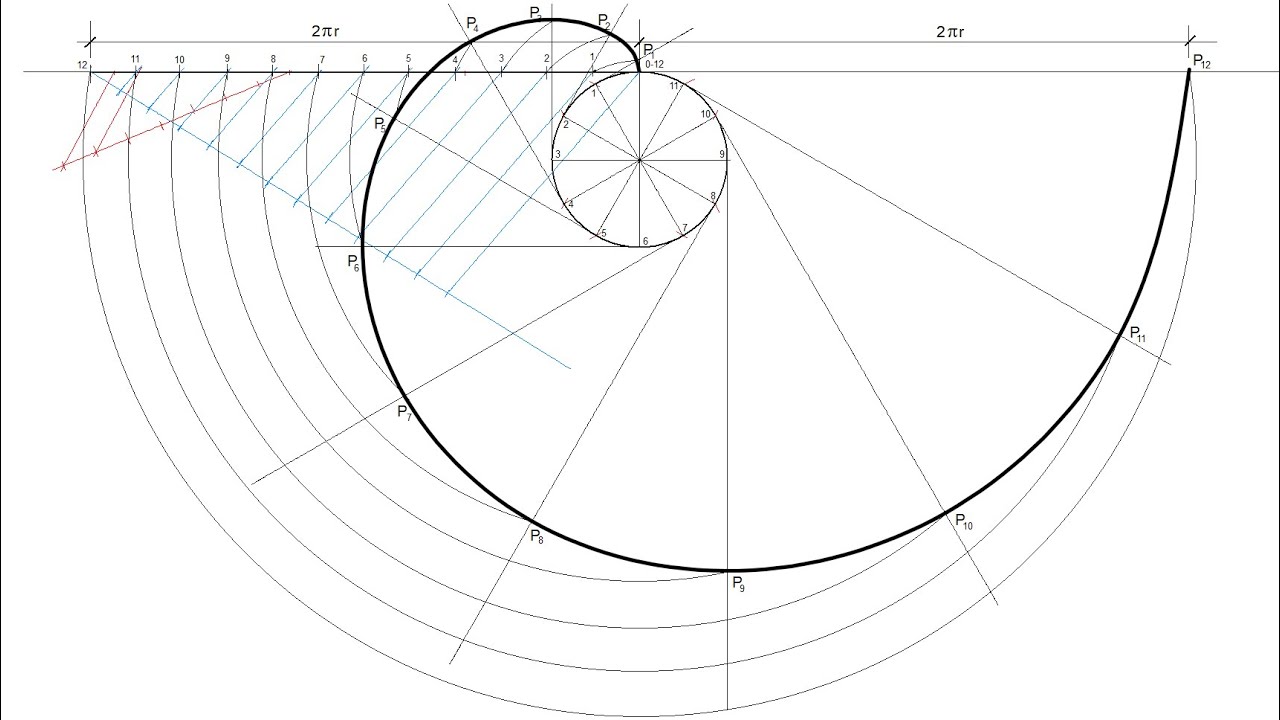
Involuta
Los dientes de los engranajes rectos tienen perfil de involuta, también llamada evolvente de circunferencia, porque garantiza una relación de transmisión constante sin deslizamiento y una transmisión de energía óptima entre los engranajes, ya que, en el punto de contacto entre dos dientes, la tangente al perfil es común a ambos dientes.
La involuta es una curva plana de desarrollo, cuyas normales son tangentes de la circunferencia. Esta circunferencia en un engranaje la define el diámetro de base (db).
A la hora de dibujar una involuta, las ecuaciones paramétrica son las más fáciles de manejar:
x (t) = \Large \frac{d_b}{2} \normalsize (cos (t) + t sin(t))
y (t) = \Large \frac{d_b}{2} \normalsize (sin (t) - t cos(t))
El radio nos sirve de referencia para elegir el parámetro t, ya que el final de la involuta lo marca el diámetro exterior (de).
r (t) = \sqrt{x^2 (t) + y^2(t)}
Curva de involuta
