Flujo Turbulento
El parámetro y+
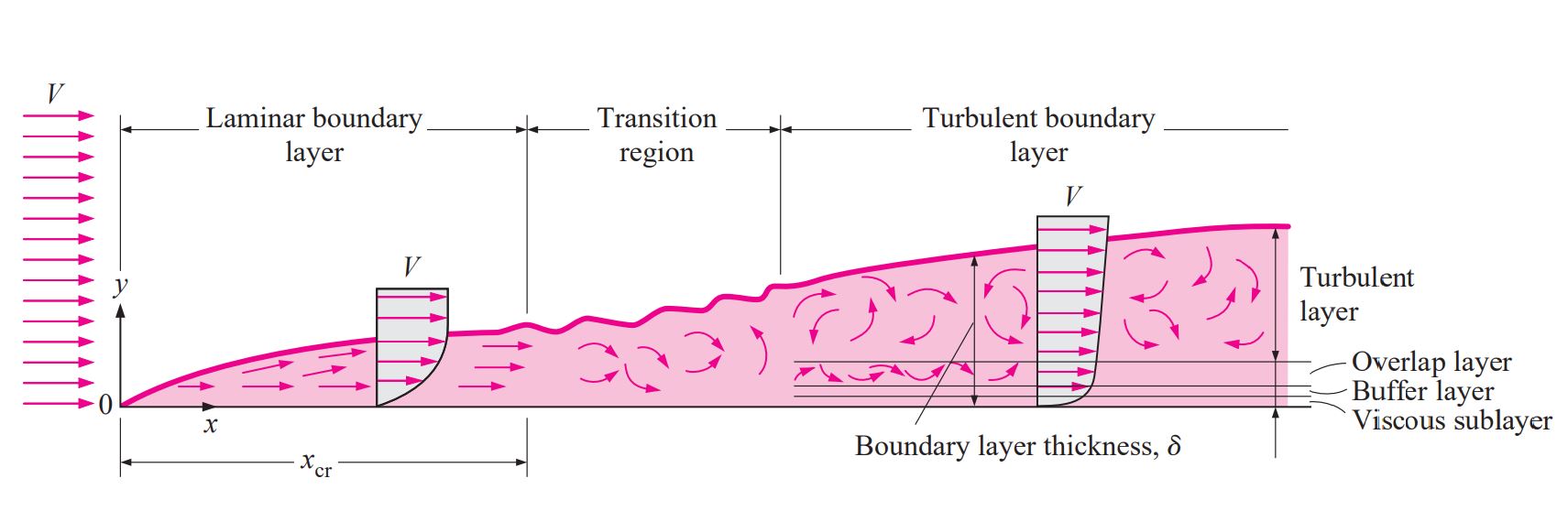
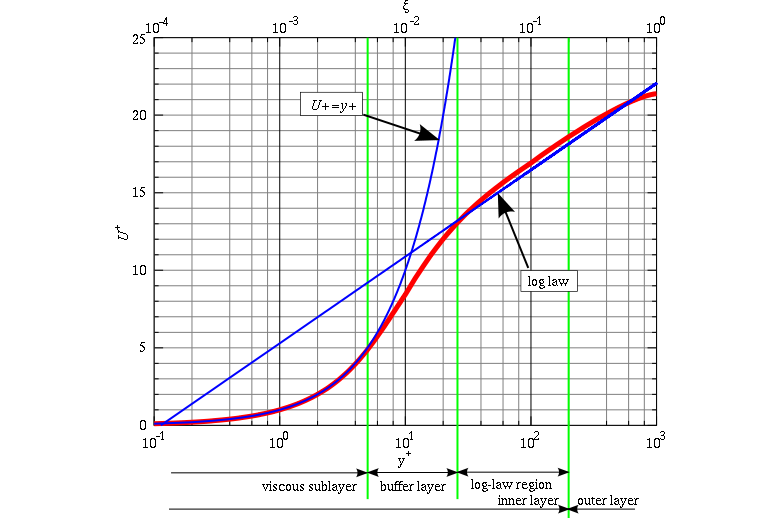
Cálculo de y+
y_p= \Large \frac {y^+ \mu} {u_{\tau} \rho}
y_H= 2 y^+
La velocidad de rozamiento ( u_{\tau} ) se calcula como:
u_{\tau} = \sqrt{ \Large \frac {\tau_{\omega}} {\rho}}
Los esfuerzos viscosos sobre la pared ( \tau_{\omega} ) dependen del coeficiente de fricción de la superficie ( C_f):
\tau_{\omega} = \Large \frac {1}{2}\normalsize \rho U^2 C_f
Donde U es la velocidad libre del fluido y el coeficiente de fricción ( C_f ) debe estimarse ya que lo desconocemos, por lo que se tomará el de una placa plana en régimen turbulento.
C_f = (2 \log_{10} (Re) - 0.65)^{-2.3}
Para flujos interiores: C_f= 0.079 Re^{-0.25}
Para flujos exteriores: C_f= 0.058 Re^{-0.2}
Re = \Large \frac {\rho U L} {\mu}
Índices de turbulencia
k = \Large \frac {3} {2} \normalsize U^2 I^2
Si se define la velocidad máxima del fluido como U_{max} , entonces la intesidad de la turbulencia ( I ), se deficne como:
I (\%) = \Large \frac {U_{max}-U} {U} \normalsize \cdot 100 = (G-1)\cdot 100
U_{max} = G \cdot U
\epsilon = C_{\mu} \Large \frac {\rho k^2}{\mu} \normalsize \beta^{-1}
Donde C_{\mu} = 0.09 en los métodos k-ϵ y k-ω, y β es el coeficiente de viscosidad turbulento.
\beta = \Large \frac{\mu_t}{\mu}
\omega = \Large \frac {\rho k}{\mu} \normalsize \beta^{-1}
| Turbulence | Re | I (%) | β |
|---|---|---|---|
| Very low | 0.05-1 | 0.1-0.2 | |
| Low | 3000-5000 | 1 | 11.6-16.5 |
| Medium | 5000-15000 | 1-5 | 16.5-26.7 |
| High | 15000-20000 | 5-20 | 26.7-34 |
| Very high | >50000 | 100 |
1< \beta < 10