Optimización del cálculo de tornillos a fatiga en coronas de giro
Garantizar la seguridad en maquinaria pesada requiere precisión absoluta. Por eso, el cálculo de tornillos a fatiga en coronas es un proceso crítico en el diseño de uniones para rodamientos de grandes dimensiones. Una unión mal calculada puede derivar en paradas costosas o accidentes graves.
En este proyecto, abordamos el reto de validar la tornillería para cargas cíclicas exigentes. Nuestro objetivo es asegurar que cada componente soporte el ciclo de vida esperado sin fallos imprevistos.
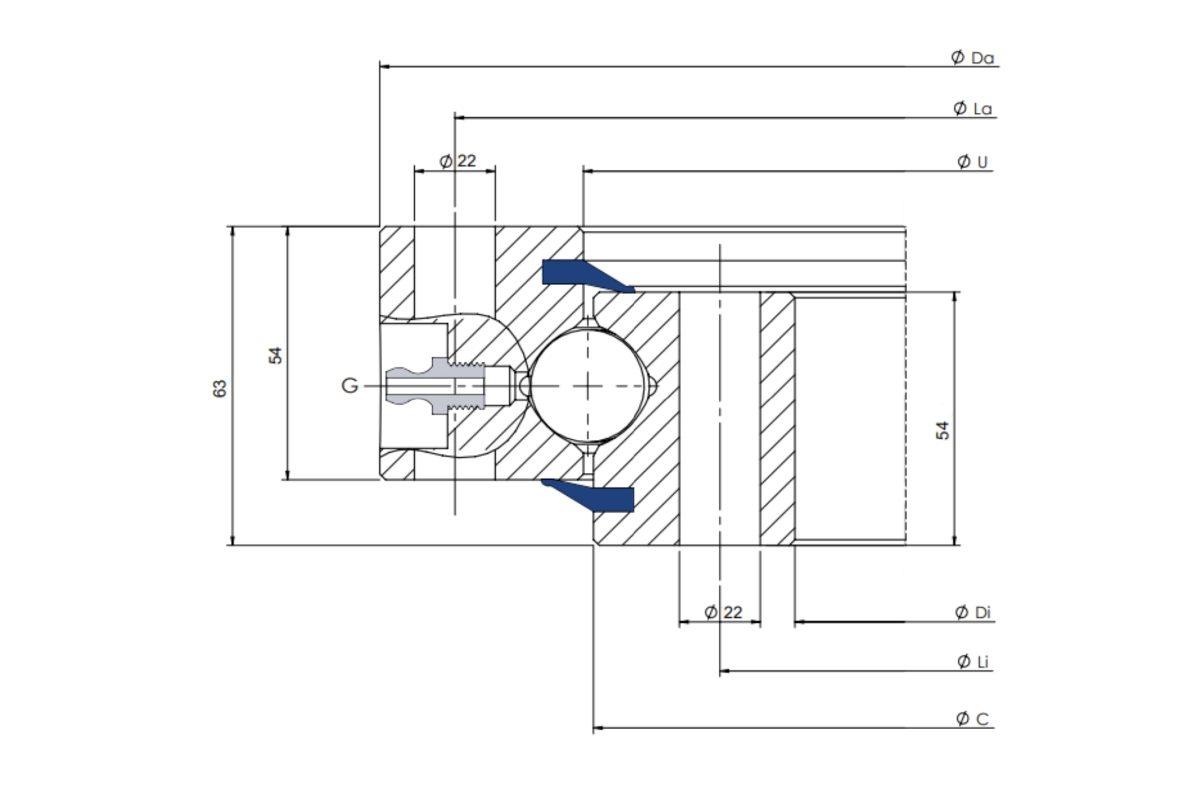
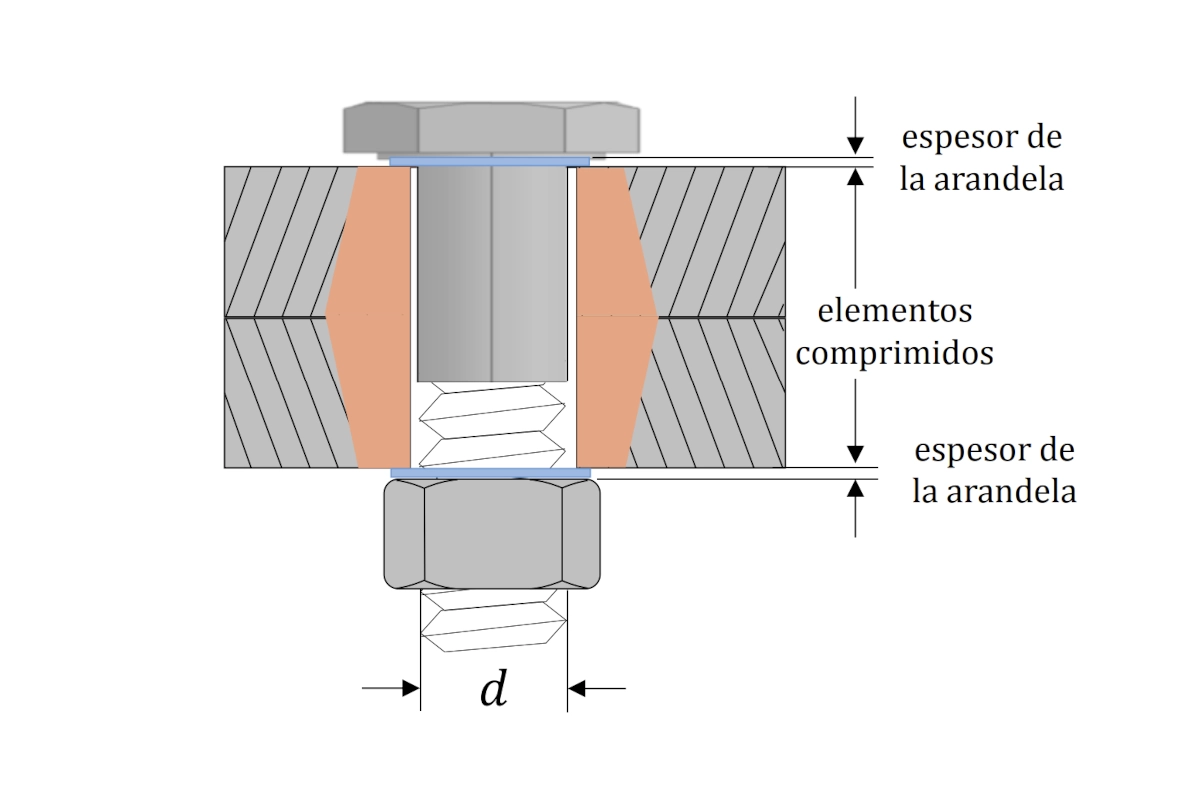
Tecma Drive S.L., referente en el sector, necesitaba un método fiable para establecer las gráficas de su tornillería. Requerían analizar calidades 8.8, 10.9 y 12.9 en las curvas de momento-carga axial (M-Ra).
Para responder a esta necesidad, en Atreydes Ingeniería hemos desarrollado una solución a medida. Se trata de una hoja de cálculo dinámica. Esta herramienta se adapta a las curvas M-Ra de los rodamientos del catálogo del cliente.
Además, sitúa los límites de las diferentes calidades de tornillería. Todo ello, respetando rigurosos criterios de cálculo estático y el imprescindible cálculo de tornillos a fatiga en coronas.
Se asume que las uniones exceden los límites si el tornillo más solicitado falla. Por tanto, los cálculos se centran en el cumplimiento de este tornillo crítico. Esto es vital en uniones sometidas a momentos, donde el esfuerzo depende de la distancia al eje.
Metodología de cálculo
Para el cálculo de tornillos a fatiga en coronas, estimamos el límite de fatiga según nuestro prontuario. Tomamos como factor de concentración de tensiones ( k_f ) el valor de 0.33.
Los tornillos presentan concentraciones de tensión en la cabeza y en la rosca. Este factor suele ser de 3 para tornillos laminados y 3.8 para mecanizados. Sin embargo, esta concentración no influye decisivamente en cargas estáticas, ya que no se suele rebasar el límite elástico.
En cambio, en el análisis de fatiga, la situación cambia. Al ser un cálculo a rotura física, se supera localmente el límite elástico. Aquí es donde los concentradores de tensión son determinantes. Para este cálculo de tornillos a fatiga en coronas, usamos un valor de concentración de 3. Esto se debe a que la mayoría se producen por laminado en frío.
k_f = \Large \frac{1}{3} \normalsize = 0.33
Establecidos los límites a vida infinita (> 10^6 ciclos), extrapolamos el valor para menos ciclos bajo cargas alternantes.
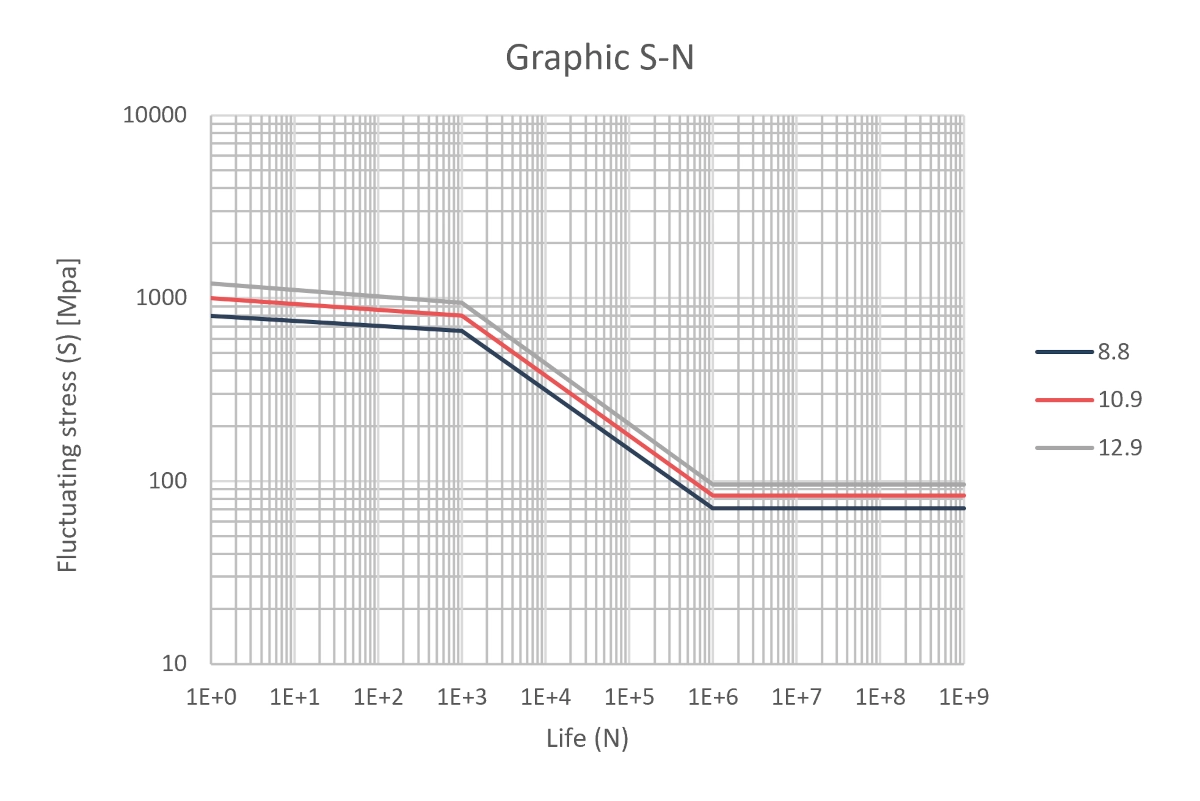
Cargas consideradas
Para ejecutar correctamente el cálculo de tornillos a fatiga en coronas, hemos considerado las siguientes cargas:
- Momento alternante ( M ) en la corona. Esto provoca tracción media y alternante por fuerzas cíclicas.
- Carga axial de compresión constante ( R_a ). Deriva del peso propio soportado por el rodamiento. Produce tensiones de compresión menores que las de tracción del momento.
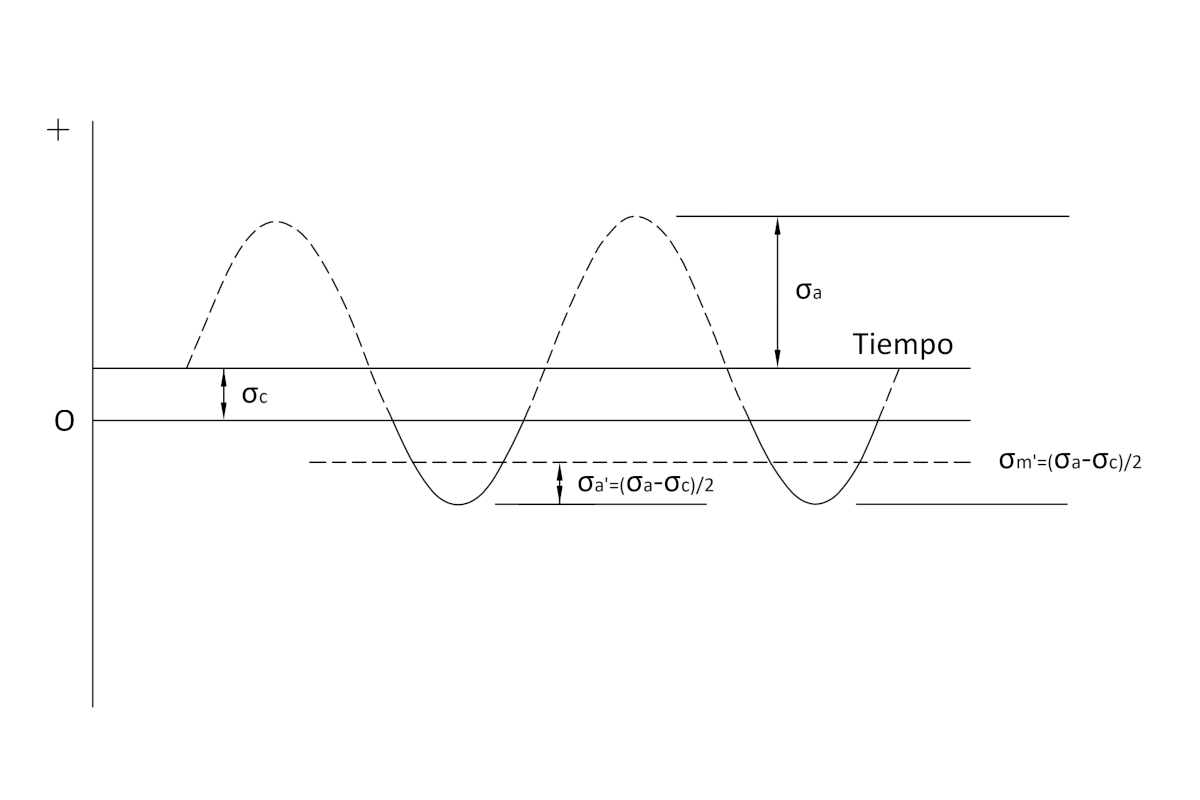
Los tornillos solo trabajan a tracción. Por ello, solo soportan tensiones medias ( \sigma'_m ) y alternantes ( \sigma'_a ) de este tipo.
Para este estado de cargas, las tensiones de tracción en la unión son:
\sigma'_a = \sigma'_m = \Large \frac{\sigma_a - \sigma_c}{2} \normalsize, para \sigma_a > \sigma_c
Donde:
- \sigma_a : tensión alternante por el momento.
- \sigma_c : tensión de compresión por carga axial.
Aunque estudiamos todas las combinaciones, esta es la más relevante para Tecma Drive S.L.
Criterios de fatiga aplicados
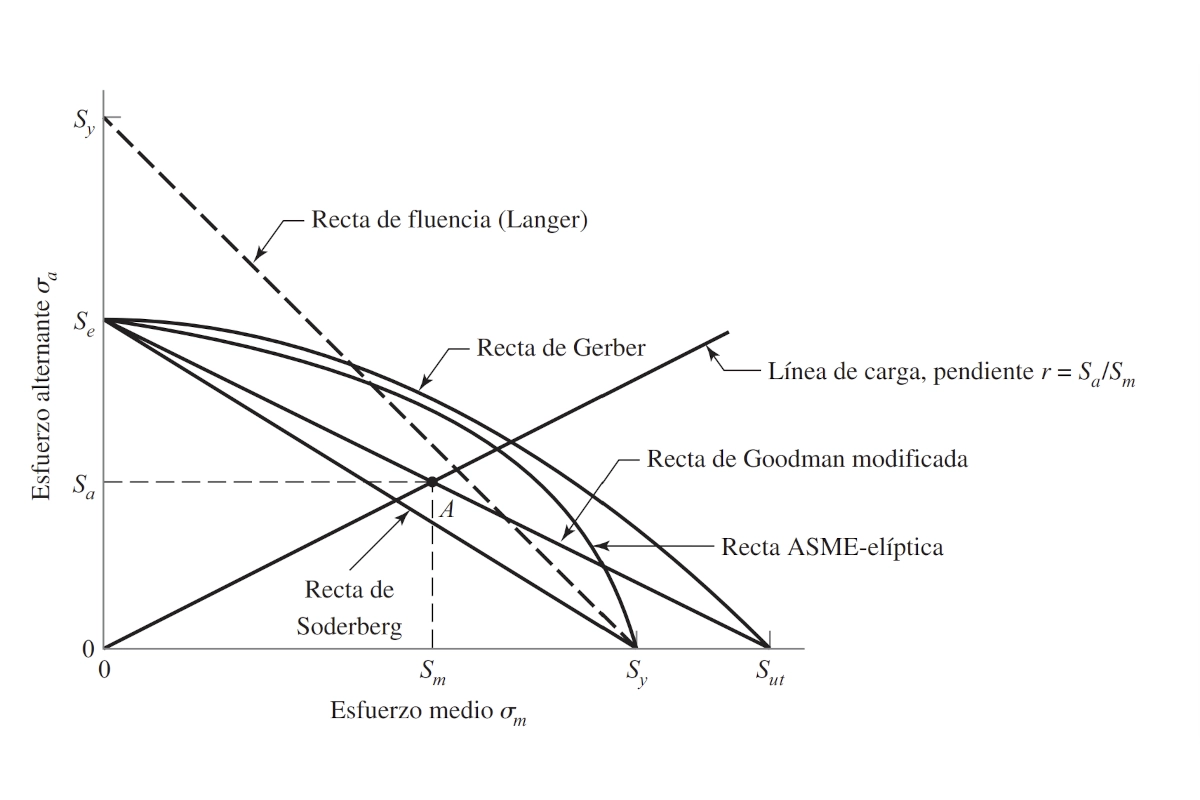
Existen varios criterios reconocidos para el cálculo de tornillos a fatiga en coronas:
1. Criterio de Soderberg
2. Criterio de Goodman modificado
3. Criterio de Gerber
4. Criterio ASME-elíptica
Las ecuaciones detalladas están en nuestro prontuario sobre Esfuerzos fluctuantes. Para este proyecto, elegimos el criterio de Soderberg. Es el más restrictivo y nos sitúa del lado de la seguridad:
\Large \frac{\sigma'_a}{S_e} \normalsize + \Large \frac{\sigma'_m}{S_y} \normalsize = 1
Sabiendo que:
\sigma'_a = \sigma'_m = \Large \frac{\sigma_a - \sigma_c}{2}
\sigma_a \Large \frac{4 M}{n \phi A_s}
\sigma_c \Large \frac{R_a}{n A_s}
Sustituyendo tensiones por cargas en la ecuación de Soderberg:
\sigma_a = \Large \frac{2 S_e S_y}{S_e + S_y} \normalsize + \sigma_c
\Large \frac{4M}{n \phi A_s} = \Large \frac{2 S_e S_y}{S_e + S_y} \normalsize + \Large \frac{R_a}{n A_s}
Reordenando, obtenemos la recta límite para la tornillería:
M = M* + \Large \frac{\phi}{4} \normalsize R_a
Donde:
M* = M_{Sod} = \Large \frac{n \phi A_s S_e S_y}{2(S_e + S_y)}
Esto indica el momento alternante de fallo a vida infinita con carga axial nula.
Podemos adaptar esta recta a otros criterios sustituyendo el momento M* :
M_{ASME-Elíptica} = \Large \frac{n \phi A_s S_e S_y}{2 \sqrt{(S_e + S_y)}}
M_{Goodman} = \Large \frac{n \phi A_s S_e S_{ut}}{2(S_e + S_{ut})}
M_{Gerber} = \Large \frac{1}{4} \normalsize n \phi A_s S^2_{ut} \left(- \Large \frac{1}{S_e} \normalsize + \Large \sqrt( \frac{1}{S^2_e} \normalsize + \Large \frac{4}{S^2_{ut}}) \right)
Variables utilizadas:
- n : número de tornillos.
- \phi : diámetro de posición.
- A_s : sección resistente.
- S_e : límite de fatiga.
- S_{ut} : tensión de rotura.
- S_y : límite elástico.
Además del cálculo de tornillos a fatiga en coronas, es imperativo verificar las cargas estáticas. Según el Eurocódigo 3, hay dos comprobaciones principales:
1. Cálculo a deslizamiento (Categoría C).
2. Cálculo a tracción (Categoría E).
Deslizamiento
La resistencia de cálculo al deslizamiento ( F_{s,RD} ) se define así:
F_{s,Rd} = \Large \frac{k_s n \mu (F_{p,C} - 0.8 F_{t,Ed})}{\gamma_{M3}}
Donde:
- k_s : parámetro del taladro (1 para normalizados).
- n : planos de deslizamiento (1 para rodamientos).
- \mu : coeficiente de rozamiento.
- F_{p,C} : fuerza de pretensado.
F_{p,C} = 0.7 S_{ut} A_s
La fuerza axial de tracción ( F_{t,Ed} ) para el tornillo más solicitado es:
F_{t,Ed} = \Large \frac{4M}{n \phi} \normalsize + \Large \frac{R_a}{n}
Este detalle es complementario al cálculo de tornillos a fatiga en coronas y asegura la integridad de la brida. El coeficiente \gamma_{M3} es 1.25. La unión cumple si:
\Large \frac {F_{s,Rd}} {F_{v,Ed}} \normalsize = \Large \frac {n F_{s,Rd}} {R_v} \normalsize > 1
Siendo R_v la fuerza cortante.
Tracción
La resistencia a tracción ( F_{t,Rd} ) según norma es:
F_{t,Rd} = \Large \frac {k_2 S_{ut} A_s} {\gamma_{M2}}
La unión resiste a tracción si se cumple la siguiente relación:
\Large \frac{F_{t,Rd}}{F_{t,Ed}} \normalsize = \Large \frac{n F_{t,Rd}}{R_a} \normalsize >1
Con R_a como el esfuerzo axial de tracción.
Resultados del estudio
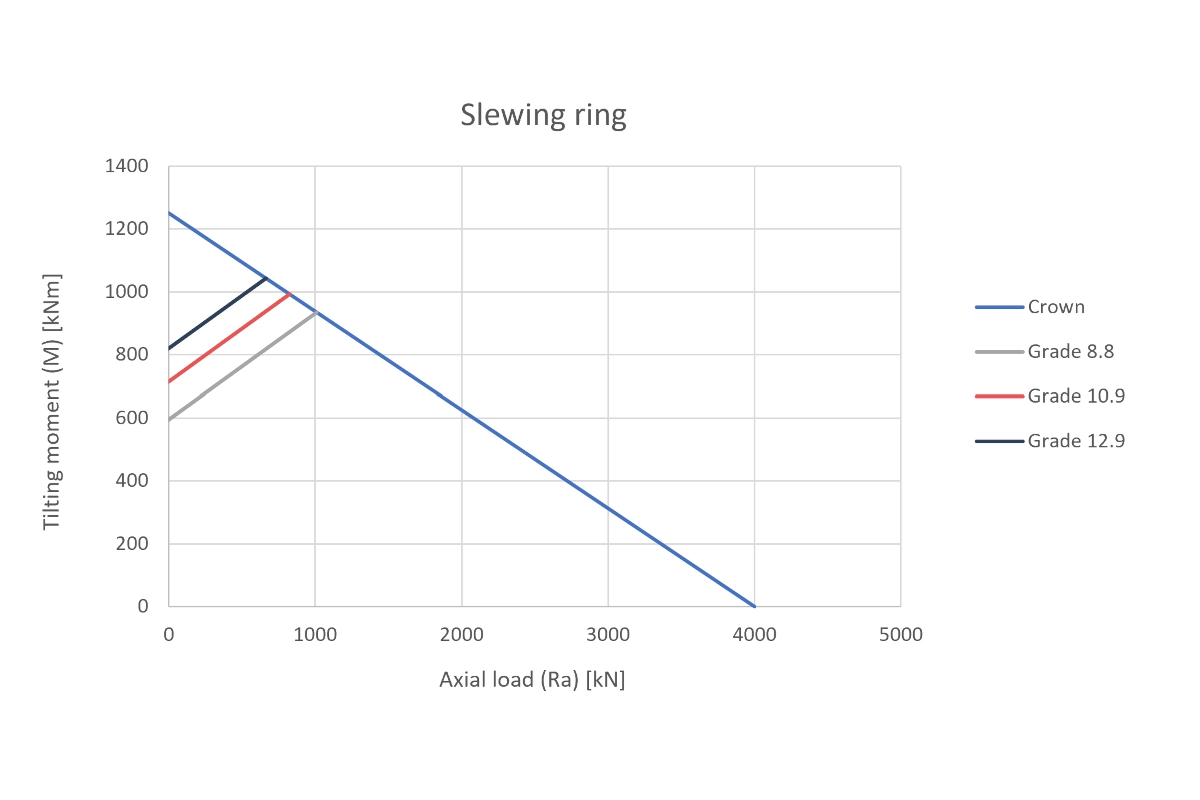
Hemos analizado tornillería de calidades 8.8, 10.9 y 12.9. El estudio abarca tanto cargas estáticas como el complejo cálculo de tornillos a fatiga en coronas para rodamientos de grandes dimensiones.
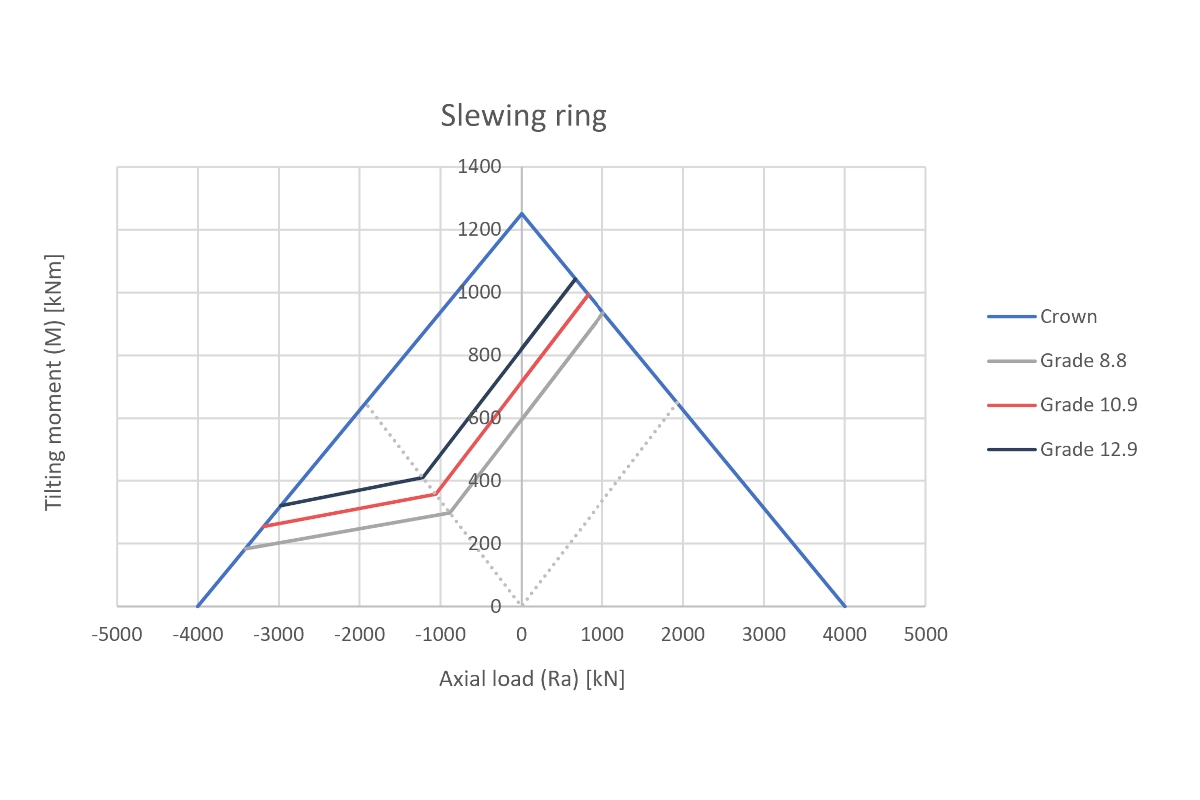
La herramienta Excel desarrollada automatiza estos procedimientos. Permite enmarcar los resultados directamente en las gráficas M-Ra de Tecma Drive S.L. A continuación, mostramos el comportamiento de los tornillos bajo tracción y compresión combinadas.
Estos resultados validan nuestro enfoque en cálculo mecánico avanzado. Si necesitas optimizar tus uniones o validar diseños críticos, puedes consultar otros casos de éxito en nuestro portafolio de proyectos
¿Necesitas ayuda con una unión compleja? Contacta con Atreydes Ingeniería y asegura la fiabilidad de tus equipos.

