Viga biapoyada con voladizos simétricos
Reacciones
F_1 = F_2 = \Large \frac{qL}{2}
Cortante
V(x) = \begin{cases} -qx & \text{for} x \le \large \frac{L-s}{2} \\ -q(x-\Large \frac{L}{2}\normalsize) & \text{for} \large \frac{L-s}{2} \normalsize < x \le \small L-\large \frac{L-s}{2} \\ -q(x+L) & \text{for} x > \small L-\large \frac{L-s}{2} \end{cases}
-V_A = V_D = \Large \frac{q (L-s)}{2}
V_B = -V_C = \Large \frac{qs}{2}
Flectores
M(x) = \begin{cases} -\large \frac{1}{2} \normalsize qx^2 & \text{for} x \le \large \frac{L-s}{2} \\ -\large \frac{1}{2} \normalsize q(x^2-Lx+L\Large\frac{L-s}{2}\normalsize) & \text{for} \large \frac{L-s}{2} \normalsize < x \le \small L-\large \frac{L-s}{2} \\ -\large \frac{1}{2} \normalsize q(x^2-2Lx+L^2) & \text{for} x > \small L-\large \frac{L-s}{2} \end{cases}
M_E = M_I = -\Large \frac{1}{8}\normalsize qL(L-s); \text{for} x = \large \frac{L-s}{2} \normalsize = \small L- \large \frac{L-s}{2}
M_G = \Large \frac{1}{2} \normalsize qL \Large (\frac{Ls}{2} \normalsize - \Large \frac{L^2}{4}) \normalsize; \text{for} x = \large \frac{L}{2}
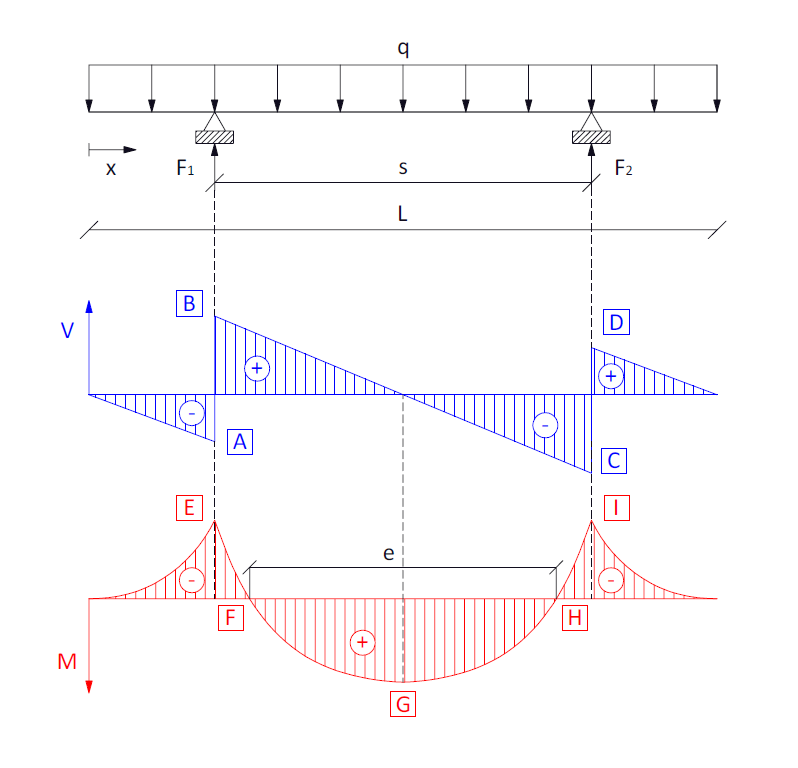
Se puede demostrar que la relación entre L y s que minimizan los momentos flectores, es decir, -M_E = M_G es:
s =f(L) : -M_E = M_G
s = \Large \frac{2}{2+\sqrt{2}} \normalsize L
La distancia e que marca la separación entre momentos nulos en los puntos F y H del vano central es:
e = \sqrt{2Ls-L^2}
Donde:
M_F = M_H = 0
x_F = \Large \frac{L-e}{2}
x_H = \Large \frac{L+e}{2}
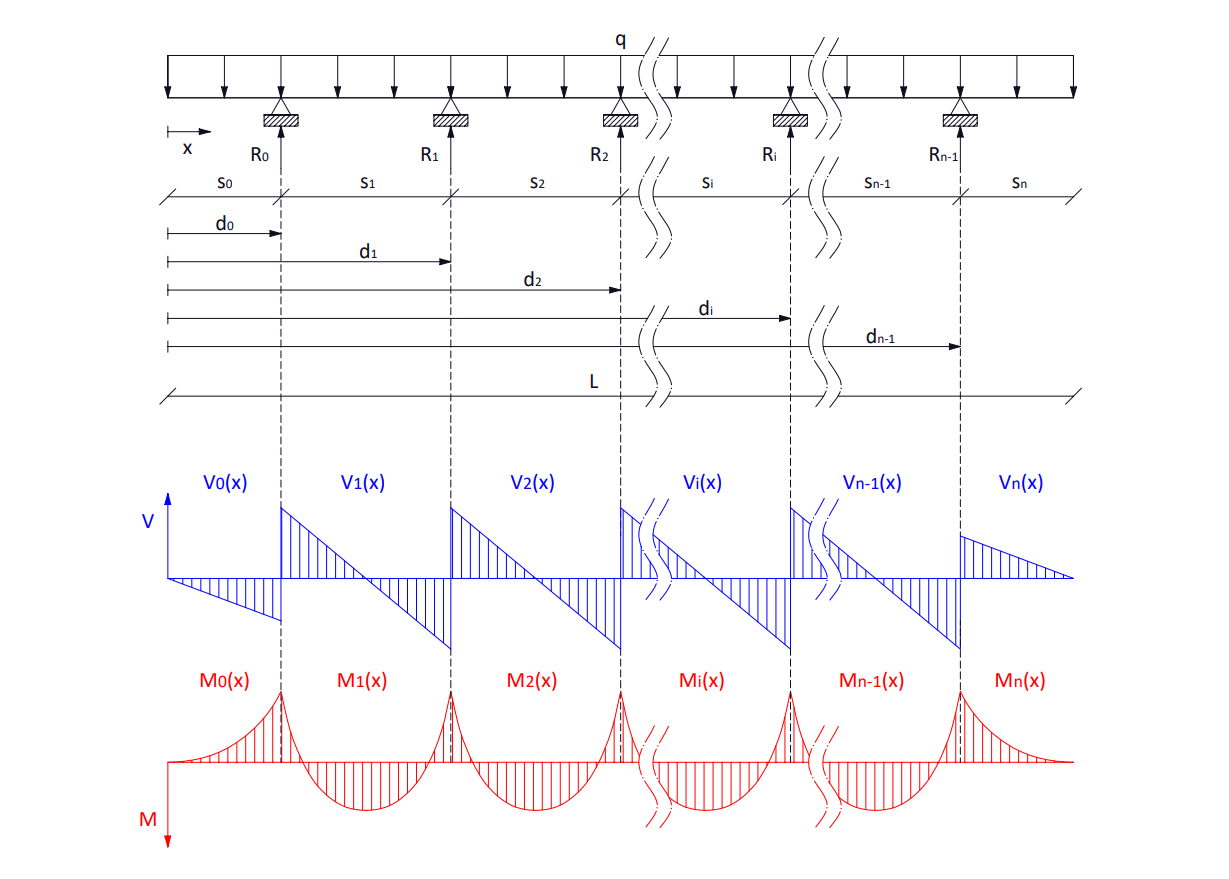
Viga multi-apoyada con voladizos
Caracterización de una viga multi-apoyada ante una carga distribuida con n tramos, 2 voladizos simétricos, n-2 vanos interiores y n-1 reacciones.
L = d_n = \sum_{i=0}^{n} s_i
d_k = \sum_{i=0}^{k} s_i
Reacciones
Debido a que se trata de un problema hiperestático, de forma aproximativa, se supondrá que cada reacción asume la mitad de la carga de cada vano adyacente, excepto las reacciones junto a los voladizos que asumirán la carga total del voladizo más la mitad de la del vano adyacente.
R_i(x) = \begin{cases} q(s_0+ \Large \frac{s_1}{2}\normalsize) & \text{for} i = 0 \\ q(\Large \frac{s_i+s_{i+1}}{2}\normalsize) & \text{for} i \in [1, n-2] \in \mathbb{N} \\ q(\Large \frac{s_{n-1}}{2}\normalsize +s_n) & \text{for} i = n-1 \end{cases}
Cortante
El subíndice k , expresa el tramo de cálculo.
k = \begin{cases} 0 & \text{para voladizo izquierdo} \\ \in [1, n-1] \in \mathbb{N} & \text{para vanos interiores} \\ n & \text{para voladizo derecho} \end{cases}
V_k(x) = \begin{cases} -qx & \text{for} k = 0 \\ -qx+\sum_{i=0}^{k-1} R_i & \text{for} k \in [1, n-1] \in \mathbb{N} \\ -q(x+L) & \text{for} k = n \end{cases}
Flectores
M_k(x) = \begin{cases} -\large \frac{1}{2} \normalsize qx^2 & \text{for} k = 0 \\ -\large \frac{1}{2} \normalsize qx^2+x\sum_{i=0}^{k-1} R_i - \sum_{i=0}^{k-1} R_i d_i & \text{for} k \in [1, n-1] \in \mathbb{N} \\ -\large \frac{1}{2} \normalsize q(x^2-2Lx+L^2) & \text{for} k = n \end{cases}
El momento máximo que se produce en el centro de cada vano puede calcularse como:
M_k(x_k) = -\large \frac{1}{2} \normalsize qx_k^2+x_k\sum_{i=0}^{k-1} R_i - \sum_{i=0}^{k-1} R_i d_i
Donde:
x_k = d_k - \Large \frac{s_k}{2}
¿Su estructura tiene geometrías complejas o cargas dinámicas?
Estas fórmulas simplificadas son válidas para pre-dimensionamiento y casos canónicos; tienen un límite.
En Atreydes Ingeniería, validamos casos no lineales en estructuras críticas, uniones complejas o fatiga, mediante Análisis por Elementos Finitos (FEA) para asegurar la optimización y seguridad.

