Beam Handbook
Two-supported beam with symmetrical cantilevers
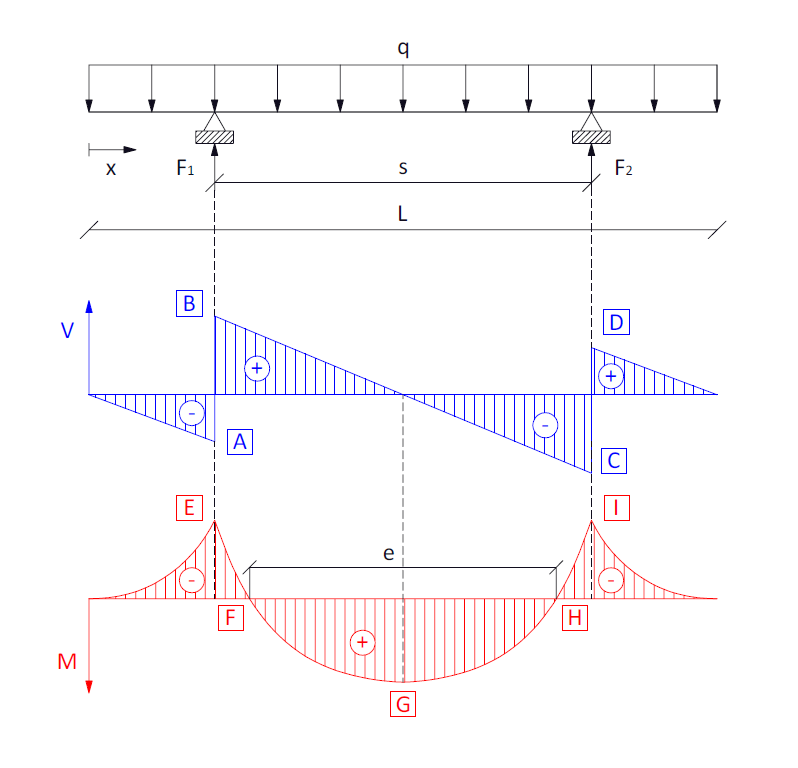
Reactions
F_1 = F_2 = \Large \frac{qL}{2}
Shear forces
V(x) = \begin{cases} -qx & \text{for} x \le \large \frac{L-s}{2} \\ -q(x-\Large \frac{L}{2}\normalsize) & \text{for} \large \frac{L-s}{2} \normalsize < x \le \small L-\large \frac{L-s}{2} \\ -q(x+L) & \text{for} x > \small L-\large \frac{L-s}{2} \end{cases}
-V_A = V_D = \Large \frac{q (L-s)}{2}
V_B = -V_C = \Large \frac{qs}{2}
Bending moments
M(x) = \begin{cases} -\large \frac{1}{2} \normalsize qx^2 & \text{for} x \le \large \frac{L-s}{2} \\ -\large \frac{1}{2} \normalsize q(x^2-Lx+L\Large\frac{L-s}{2}\normalsize) & \text{for} \large \frac{L-s}{2} \normalsize < x \le \small L-\large \frac{L-s}{2} \\ -\large \frac{1}{2} \normalsize q(x^2-2Lx+L^2) & \text{for} x > \small L-\large \frac{L-s}{2} \end{cases}
M_E = M_I = -\Large \frac{1}{8}\normalsize qL(L-s); \text{for} x = \large \frac{L-s}{2} \normalsize = \small L- \large \frac{L-s}{2}
M_G = \Large \frac{1}{2} \normalsize qL \Large (\frac{Ls}{2} \normalsize - \Large \frac{L^2}{4}) \normalsize; \text{for} x = \large \frac{L}{2}
It can be proved that the relation between L and s that minimize the bending moments, i.e., -M_E = M_G is:
s =f(L) : -M_E = M_G
s = \Large \frac{2}{2+\sqrt{2}} \normalsize L
The distance e that marks the separation between null moments at points F and H on the central span is:
e = \sqrt{2Ls-L^2}
Where:
M_F = M_H = 0
x_F = \Large \frac{L-e}{2}
x_H = \Large \frac{L+e}{2}
Multi-supported beam with cantilevers
Characterization of a multi-supported beam under a distributed load with n spans, 2 cantilevers, n-2 inner spans and n-1 reactions.
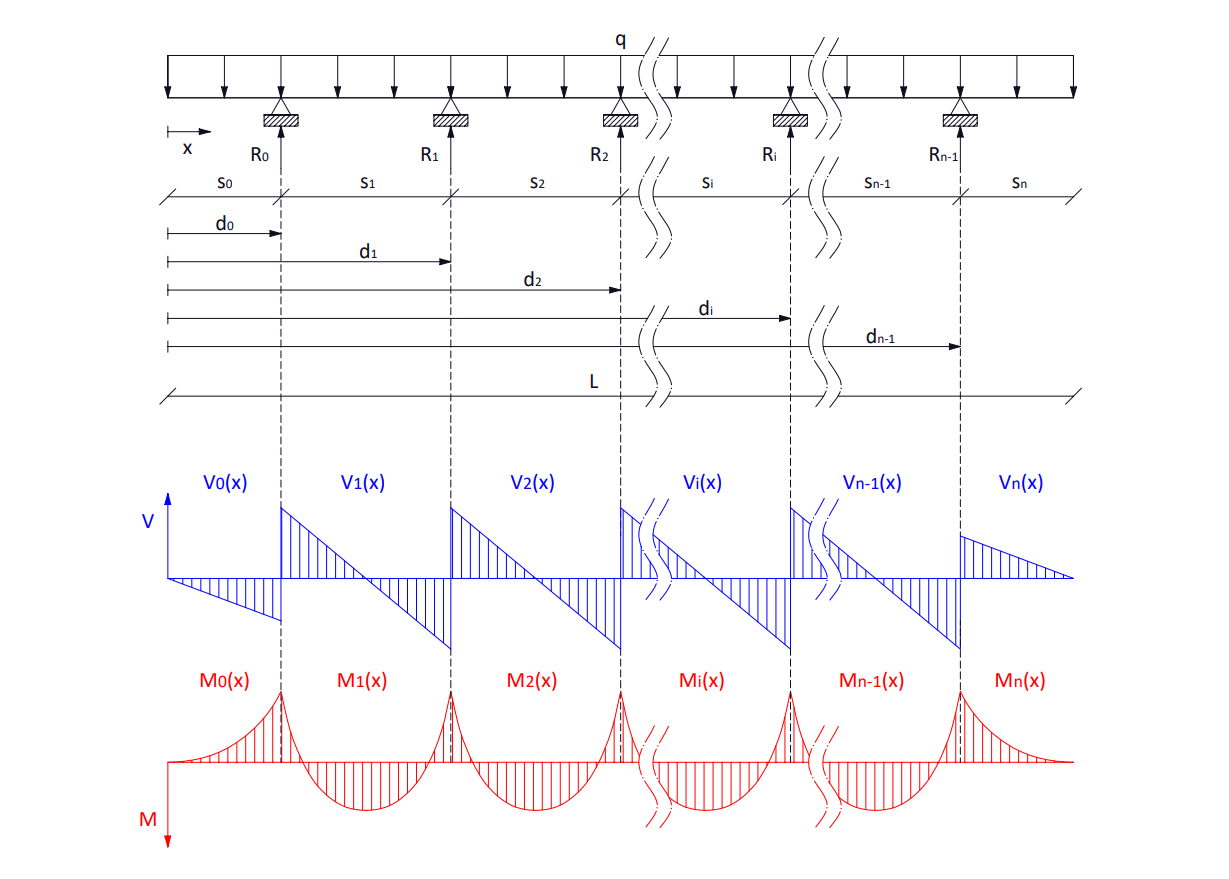
L = d_n = \sum_{i=0}^{n} s_i
d_k = \sum_{i=0}^{k} s_i
Reactions
Since this is a hyperstatic problem, it will be assumed, approximately, that each reaction assumes half of the load on each adjacent span, except for the reactions next to the cantilevers, which will take the total load of the cantilever plus half of that on the adjacent span.
R_i(x) = \begin{cases} q(s_0+ \Large \frac{s_1}{2}\normalsize) & \text{for} i = 0 \\ q(\Large \frac{s_i+s_{i+1}}{2}\normalsize) & \text{for} i \in [1, n-2] \in \mathbb{N} \\ q(\Large \frac{s_{n-1}}{2}\normalsize +s_n) & \text{for} i = n-1 \end{cases}
Shear forces
The subindex k expresses the calculation span.
k = \begin{cases} 0 & \text{for left cantilever} \\ \in [1, n-1] \in \mathbb{N} & \text{for inner span} \\ n & \text{for right cantilever} \end{cases}
V_k(x) = \begin{cases} -qx & \text{for} k = 0 \\ -qx+\sum_{i=0}^{k-1} R_i & \text{for} k \in [1, n-1] \in \mathbb{N} \\ -q(x+L) & \text{for} k = n \end{cases}
Bending moments
M_k(x) = \begin{cases} -\large \frac{1}{2} \normalsize qx^2 & \text{for} k = 0 \\ -\large \frac{1}{2} \normalsize qx^2+x\sum_{i=0}^{k-1} R_i - \sum_{i=0}^{k-1} R_i d_i & \text{for} k \in [1, n-1] \in \mathbb{N} \\ -\large \frac{1}{2} \normalsize q(x^2-2Lx+L^2) & \text{for} k = n \end{cases}
The maximum moment produced at the middle of each inner span can be calculated as follows:
M_k(x_k) = -\large \frac{1}{2} \normalsize qx_k^2+x_k\sum_{i=0}^{k-1} R_i - \sum_{i=0}^{k-1} R_i d_i
Where:
x_k = d_k - \Large \frac{s_k}{2}