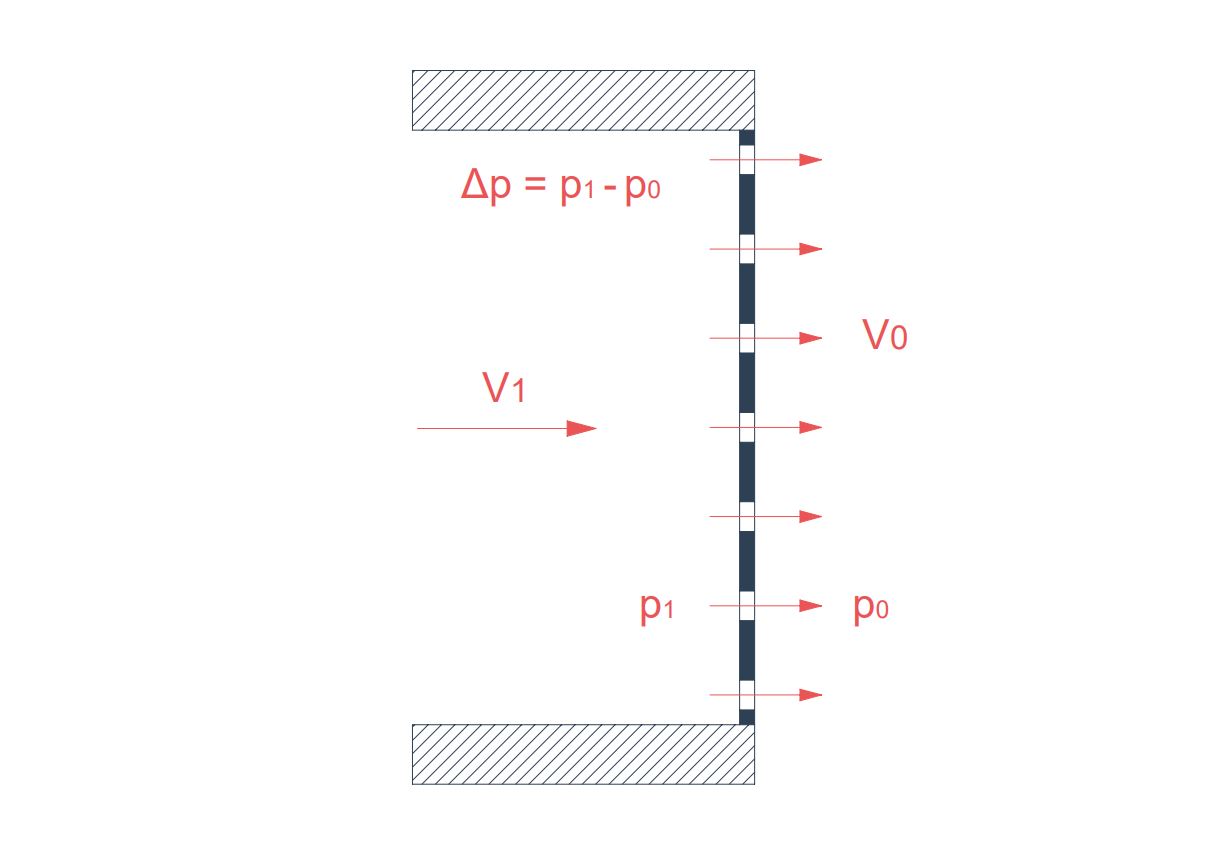
Pressure drop for thin perforated plates
It is defined the pressure drop coefficient ( \zeta ) as:
\zeta = \Large \frac {\Delta p}{\frac{1}{2} \rho V_1}
Where:
- \Delta p : pressure drop through the plate.
- V_1 : air velocity on the upstream face of the plate.
- \rho : air density.
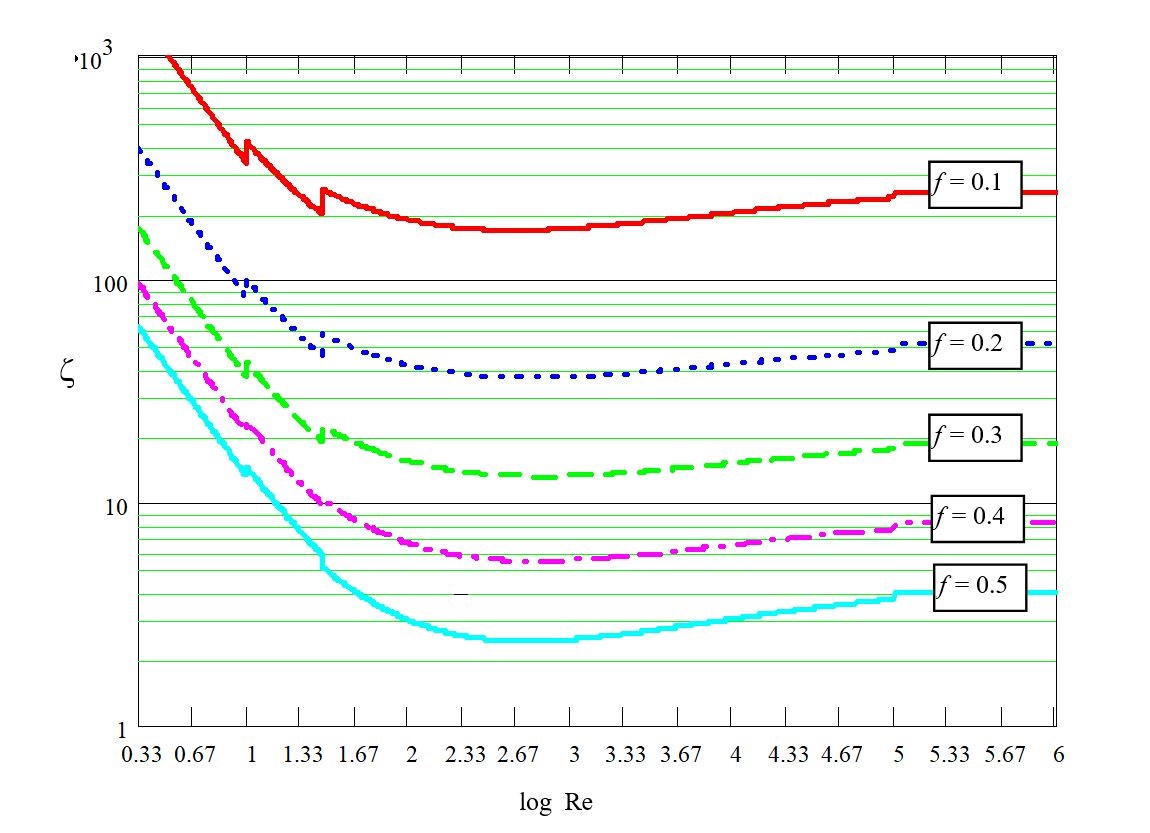
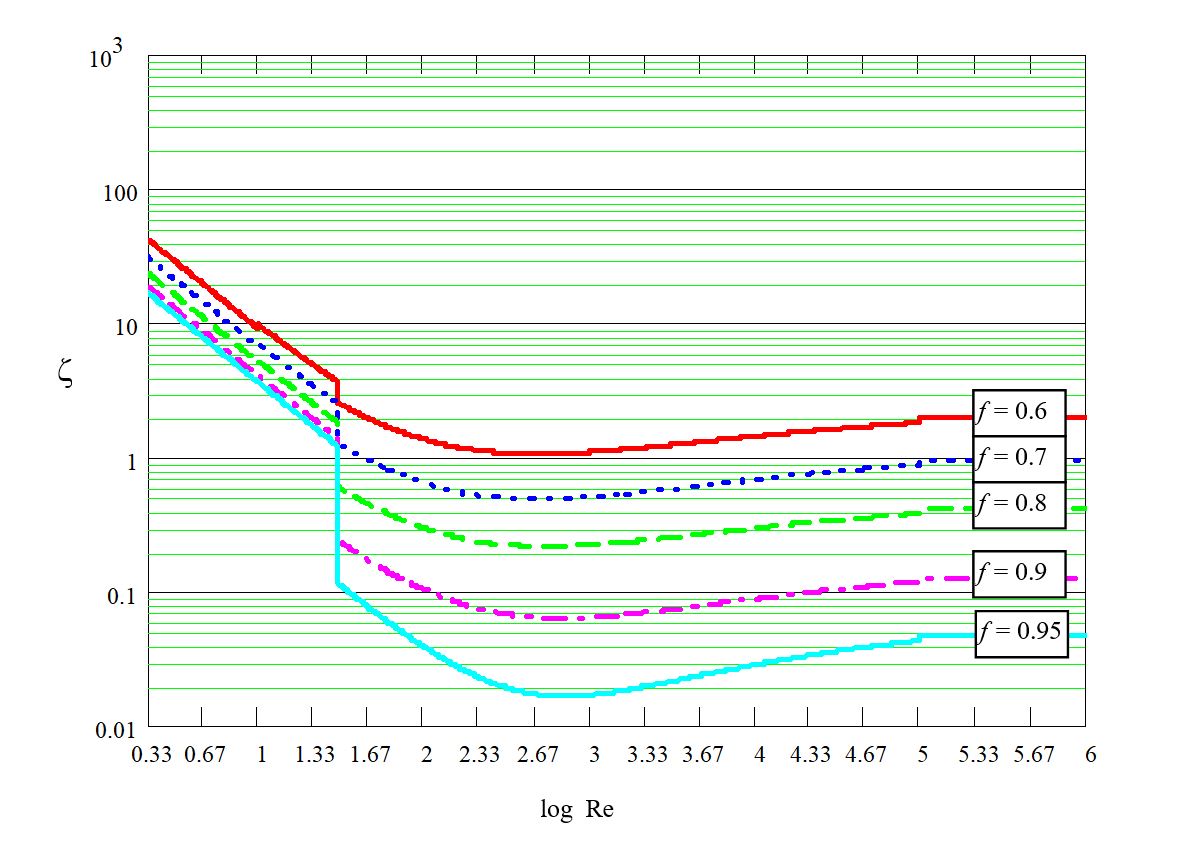
Pressure drop coefficient ( \zeta ) is function of the open area fraction or porosity ( f ) and the Reynolds number ( Re ). Porosity ( f ) is a factor whose values move between 0 and 1; f = 1 means a fictitious 100% open plate:
Re = \Large \frac{V_0 d_h}{\nu}
Where:
- V_0 : air velocity in the orifices.
- d_h : hydraulic diameter or length scale.
- \nu : air cinematic viscosity.
If we assume circular orifices the geometrical diameter is equal to the hydraulic diameter.
We can use the equation of continuity:
f V_0 = V_1
to get the Reynolds number ( Re ) from the approach velocity ( V_1 ):
Re = \Large \frac{V_1 d_h}{f \nu}
Depending on the Reynold number ( Re ), it is applied the corresponding formula or diagram for the four possible regimes:
| Regime | Reynolds | ζ |
|---|---|---|
| Turbulent | Re ≥ 10^5 | ζ= ζ (diag.1-2) |
| Transitional | 30 ≤ Re < 10^5 | |
| 10 ≤ Re < 30 | ||
| Laminar | Re < 10 | ζ = 30/(f² Re) |
Diagrams are expressed in a double logarithmic system.