Gears
Geometría
| Module | |
|---|---|
| Preferred | 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50 |
| Next Choise | 1.125, 1.375, 1,75, 2.25, 3.5, 4.5, 5.5, 7, 9, 11, 14, 18, 22, 28, 36, 45 |
\large d = m \cdot z
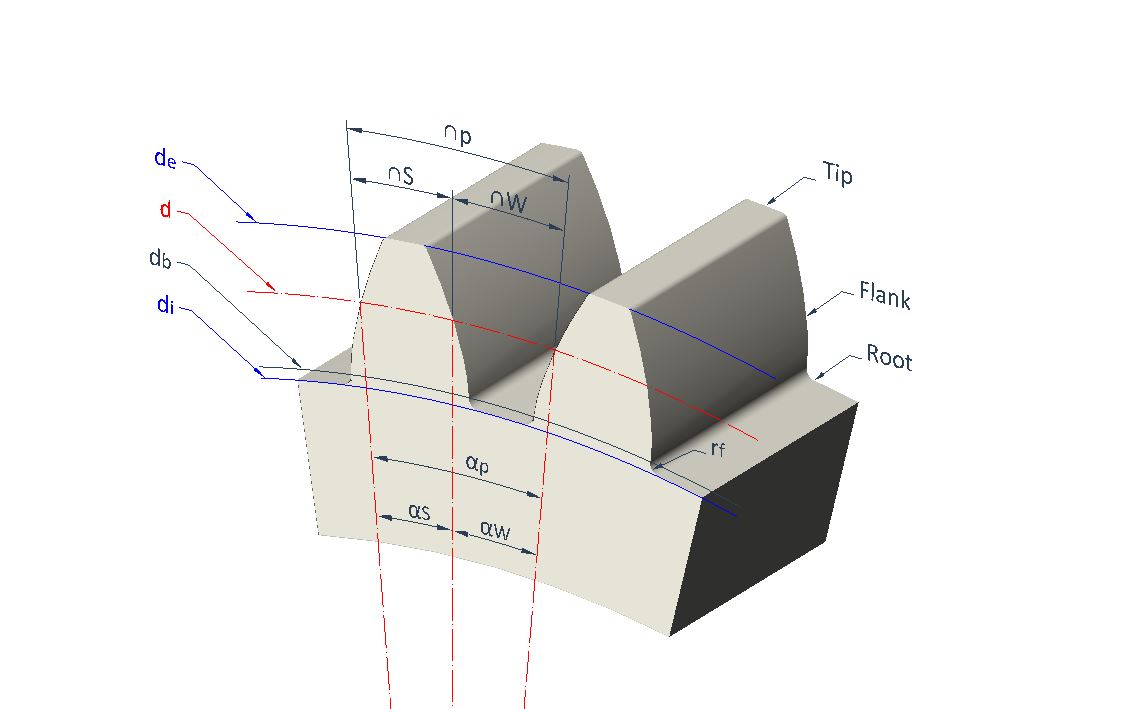
\normalsize p = \Large \frac{\pi d}{z}
\normalsize S = p \Large \frac {19}{40}
\normalsize W = p \Large \frac {21}{40}
\normalsize \alpha_p (º) = \Large \frac{2 p}{d} \frac{180}{\pi}
\normalsize \alpha_S (º) = \Large \frac{2 S}{d} \frac{180}{\pi}
\normalsize \alpha_W (º) = \Large \frac{2 W}{d} \frac{180}{\pi}
\normalsize d_b = d cos(\phi)
\normalsize d_e = d +2m
\normalsize d_i = d -2.5m
\normalsize r_f \approx 0.25m
\normalsize l = \frac {1}{2}(d_e-d_i)
Gearing Condition
\large m_1 = m_2
Gear Ratio
r_t = \Large \frac {\omega_2}{\omega_1} \normalsize = \Large \frac {d_1}{d_2} \normalsize = \Large \frac {z_1}{z_2}
Contact Ratio
\varepsilon = \Large \frac {L \tiny AB}{p cos (\phi)} \normalsize> 1.2
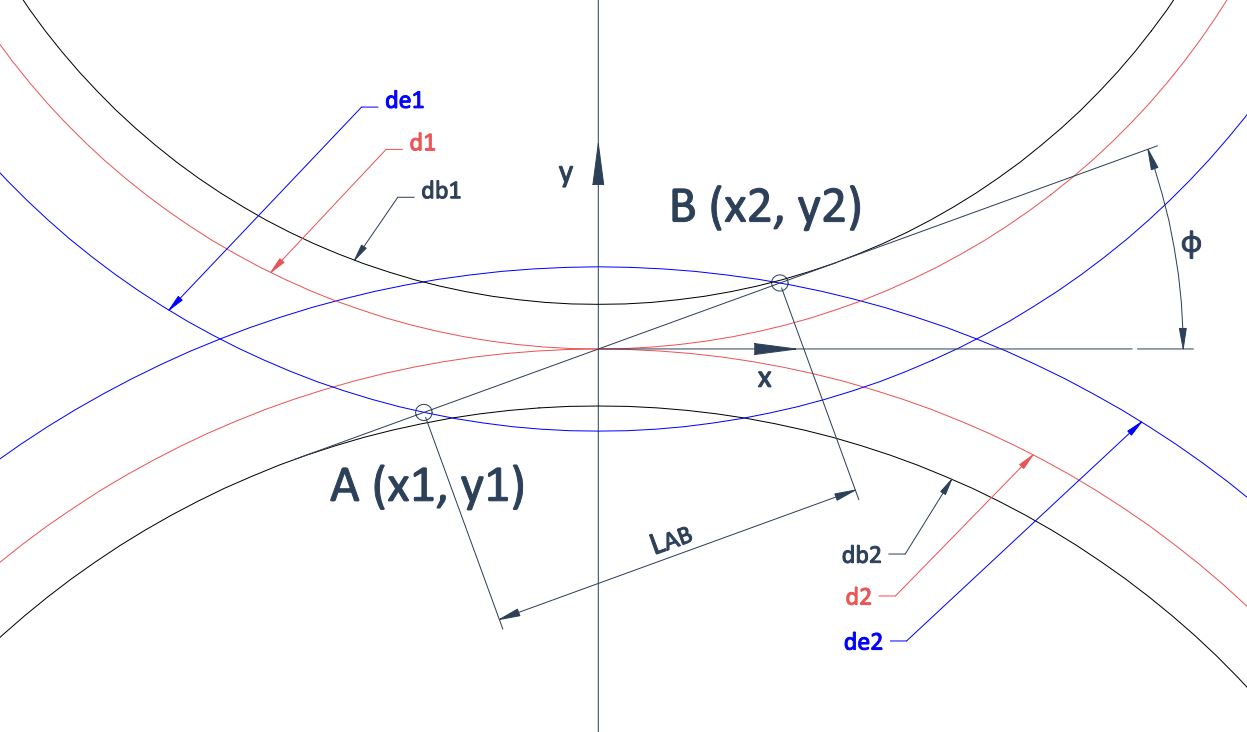
L \tiny AB \normalsize = d(A,B) = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}
Interference
Z_{P1} = \Large \frac{2(k)}{3sin^2(\phi)} \normalsize (1+\sqrt{1+3sin^2(\phi)}) = 12.3 = 13 teeth
Z_{Pn} = \Large \frac{2(k)}{(1+2n) sin^2(\phi)} \normalsize (n+\sqrt{n^2+(1+2n) sin^2(\phi)})
Z_{ge} = \Large \frac{Z_{pe}^2 sin^2(\phi)-4k^2}{4k-2Z_{pe}sin^2(\phi)}
| n | Zpn | Zgn |
|---|---|---|
| 1 | 13 | 13 |
| 2 | 15 | 30 |
| 3 | 15 | 45 |
| 4 | 16 | 64 |
| 6 | 16 | 96 |
| 7 | 17 | 119 |
| 77 | 17 | 1309 |
| 78 | 18 | 1404 |
| 90 | 18 | 1620 |
| 100 | 18 | 1800 |
| Zpe | Zge |
|---|---|
| 10 | 4 |
| 11 | 7 |
| 12 | 10 |
| 13 | 16 |
| 14 | 26 |
| 15 | 45 |
| 16 | 101 |
| 17 | 1309 |
| 18 | No limit |
Z_{Pr} = \Large \frac{2(k)}{sin^2(\phi)} \normalsize = 17.1 = 18 teeth
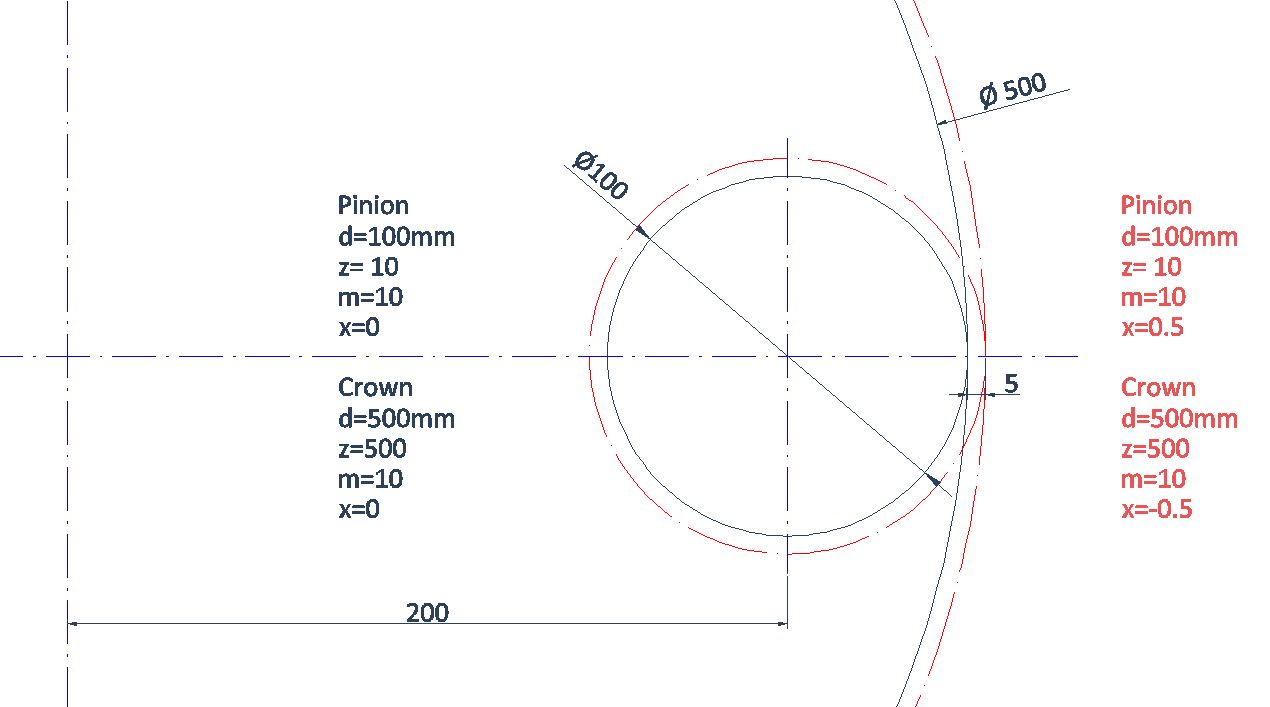
Shifted Gears

d' = d + 2 m x for external gears
d' = d - 2 m x for internal gears
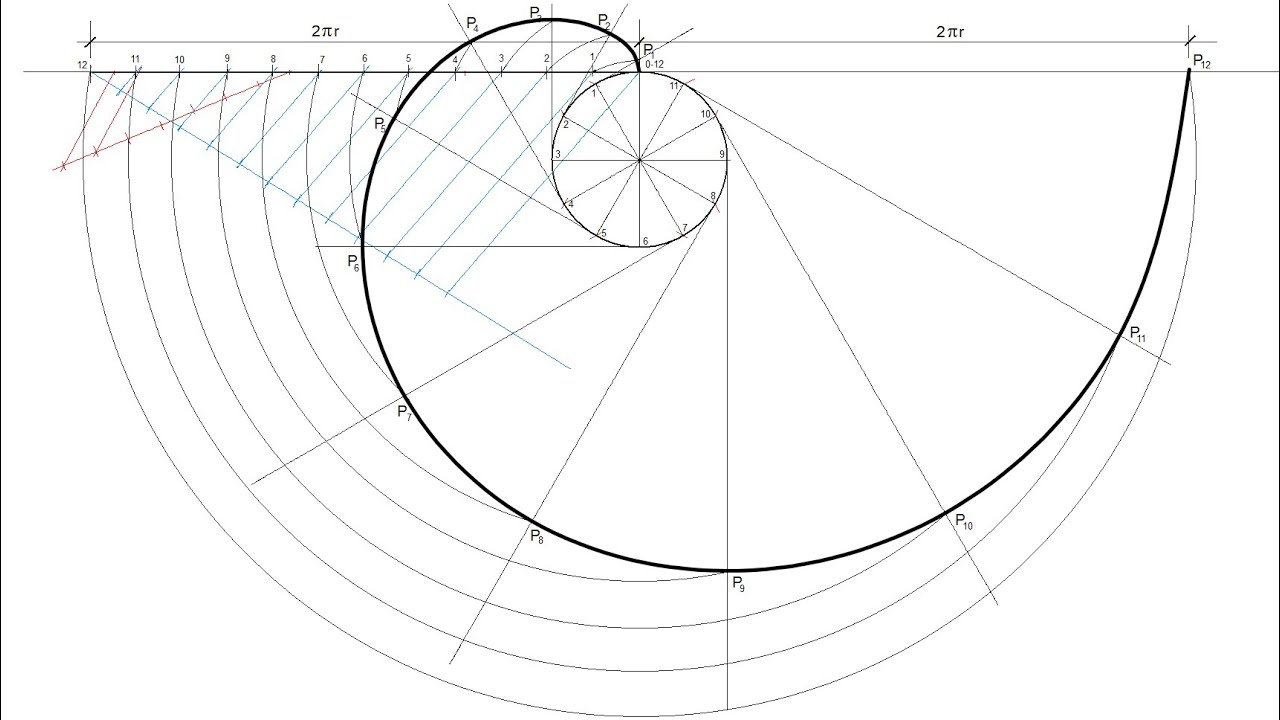
Involute
x (t) = \Large \frac{d_b}{2} \normalsize (cos (t) + t sin(t))
y (t) = \Large \frac{d_b}{2} \normalsize (sin (t) - t cos(t))
r (t) = \sqrt{x^2 (t) + y^2(t)}