Odalys Campus

Failure in any mechanical or structural system can mean that a part has separated into two or more pieces; it has become permanently distorted, thus ruining its geometry; its reliability has been degraded; or its function has been compromised, for whatever reason.

Structural material performance is typically classified as either ductile or brittle. Typically, materials are classified as ductile when the unit strain at the breaking point ( \epsilon_f ) is greater than 0.05 and when they have an identifiable yield strength that is often the same in tension as in compression ( S_{yt} = S_{yt} = S_y ). Brittle materials, \epsilon_f < 0.05, have no identifiable yield strength and are typically classified by ultimate tensile ( S_{ut} ) and compressive (S_uc) strengths. identifiable creep and are typically classified by ultimate tensile ( S_{ut} ) and compressive ( S_{uc} ) strengths.

Von Mises theory ( \sigma_{VM} ) is applied to prevent yield failure of the material. This theory, considered to be the most appropriate for the failure of ductile materials, states that material yield failure will not occur if the equivalent von Mises stress does not exceed the yield limit of the material, reduced by a safety coefficient ( \gamma ):

\sigma_{VM} \leq S_y' = \Large \frac{S_y}{\gamma}

Where:

• \sigma_{MV} : von Mises stress.
• \S_y : material yield stress
• \gamma : reduction coefficient, usually of value 1.05
• \S_y' : corrected yield stress

Therefore, the validation of results by this criterion requires the quantification of stress levels through the determination of equivalent Von Mises stress, which results from the combination of principal stresses, and is determined by the equation:

\sigma_{MV} = \sqrt{\Large \frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}}

To apply this theory, the material performance is idealized as elastic, i.e., whatever the stress level, the analysis will be based on the hypothesis that the stress-strain material performance is linear (stress-strain proportionality):

\sigma = E  \epsilon;    \forall \epsilon < \epsilon_y

\epsilon_y = \Large \frac{\sigma_y}{E}

With:

• E : material elastic modulus
• \epsilon : unit strain
• \epsilon_y : unit strain at yield stress
• \sigma : stress
• \sigma_y : yield stress limit

Where:

• S_y : yield strength defined by unit strain a.
• S_u : ultimate strength limit
• S_f : ultimate fracture limit
• \epsilon_y : unit strain at yield point
• \epsilon_u : unit strain at resistant point
• \epsilon_f : unit strain at racture point
• pl : proportionality limit
• el : yield limit

Using the xyz components of the three-dimensional stress, von Mises stress can be written as:

\sigma_{MV} = \sqrt{\Large \frac{(\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+6 (\tau_x^2+\tau_y^2+\tau_z^2)}{2}}

The maximum normal stress theory (ENM) stipulates that failure occurs when one of the three principal stresses equals or exceeds the strength. If the principal stresses of a general state of stress are placed in the ordered form \sigma_1 > \sigma_2 > \sigma_3 , this theory predicts that failure occurs when \sigma_1 \geq S_{ut} or \sigma_3 \leq -S_{uc} , where S_{ut} and S_{uc} are tensile and compressive strengths, respectively, given as positive quantities.

Since yield stress ( S_y ) is very close to the strength ( S_u ) in brittle materials, the following will be assumed as validation criteria:

\sigma_{MV} \leq \Large \frac {1}{\gamma} \normalsize  min (S_{ut}, S_{uc})

Where:

• S_{ut} : tensile fracture strength of the material.
• S_{uc} : compressive fracture strength of the material
• S_u' : corrected ultimate limit of fracture

The following are the physical properties of the materials used in this project for the components described:

• Aluminum 6063-T5: Guides, glass brackets, L-shaped anchors.
• Tempered glass: photovoltaic panels

Engineering unit is subjected to its own weight and wind loads.

Once the material properties of each element in the engineering unit have been established in the engineering unit, the self-weight loads are established. The most restrictive wind loads affecting the system according to the Technical Building Code (CTE) are determined below.

Basic wind speed ( v_b ) for this site is 26m/s.

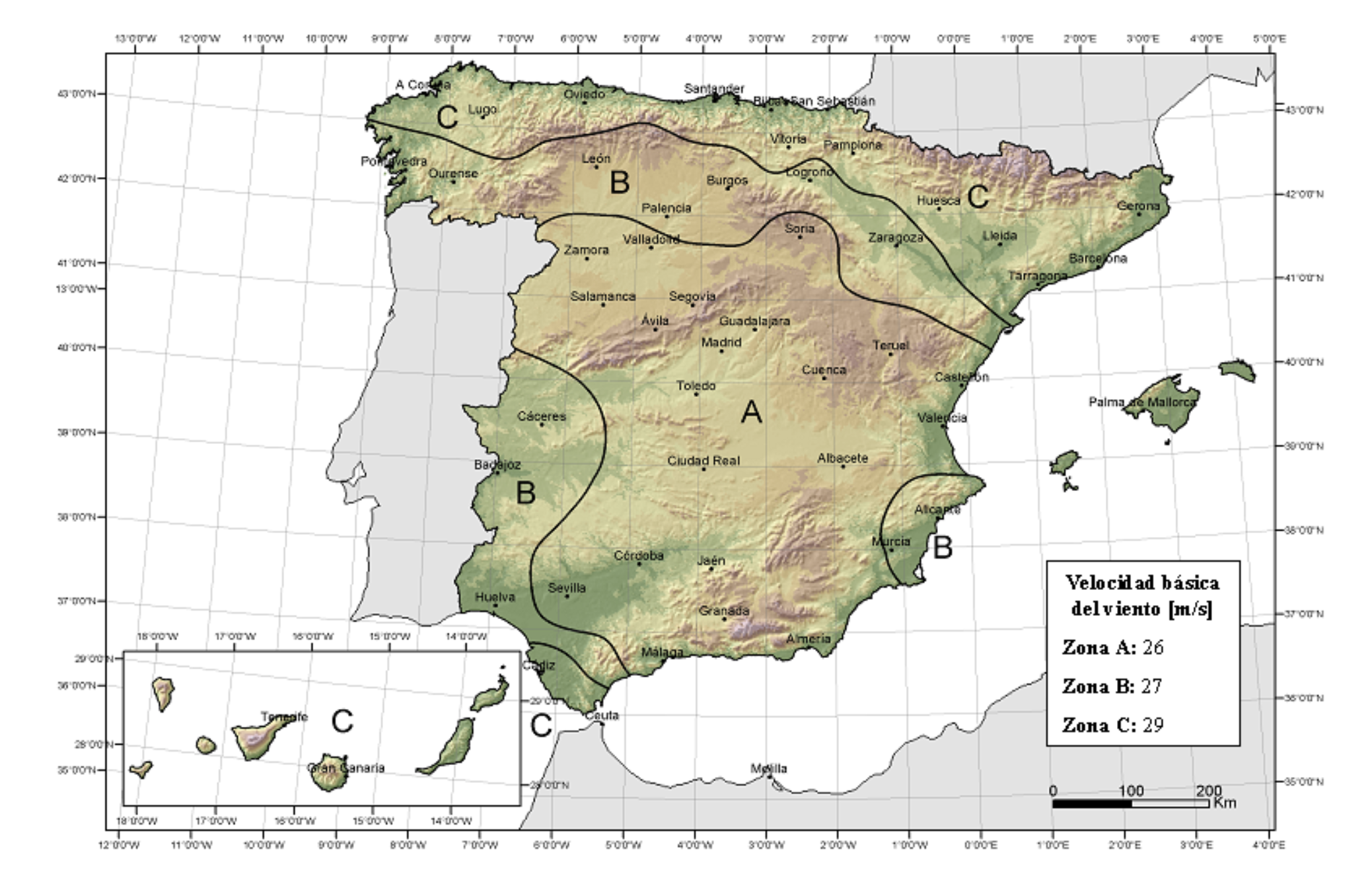
According to CTE, pressure w provided by the wind, can be calculated as follows:

w = q_{ref}  C_e(z)  C_p

Being:

q_{ref} = \Large \frac{1}{2}\normalsize \rho v_b^2

With \rho as the wind density at 1.25kg/m³.

The height of the building (18 meters) in type IV terrain has been considered In the calculation of the exposure coefficient ( C_e ).

With these values, the parameter C_e is 2.20.

The external pressure coefficients ( C_p ) shall be taken from table D3 Vertical parameters for buildings of document DB SE-AE Actions in the building (CTE):

For a surface larger than 10m², as in our case, the maximum external pressure coefficients ( C_e ) for our engineering unit are 0.8 in the pressure cases and -1.2 for the suction cases.

Since the suction coefficient is higher than the pressure one, and because certain connections, such as bolts and anchor bolts, are calculated at tensions that appear due to suction winds, we will calculate our engineering unit in these cases. If all components withstand such suction loads, we can ensure that they will also do so in cases where the wind acts in pressure.

Also, we must increase this load with the safety coefficients dictated by the CTE in its document DB SE Structural Safety, in Table 4.1 Partial safety coefficients ( \gamma ) for actions, where this coefficient is 1.5 for unfavourable variable actions in persistent or transitory situations.

With all these considerations our design wind load will be:

P_v = \gamma  \Large \frac{1}{2}\normalsize  \rho  v_b^2  C_e(z)  C_p

P_v = 1.5  ·  \Large \frac{1}{2}\normalsize  · 1.25  ·  26^2  ·  2.2  ·  (-1.2) = -1673 N/mm^2