Desprendimiento de vórtices en seguidores solares
Las oscilaciones inducidas por el desprendimiento de vórtices en seguidores solares son debidas a un efecto de vibración asociado a la calle de vórtices que se forma en su estela. En una planta fotovoltaica, a diferencia del galope y divergencia torsional, el desprendimiento de vórtices se produce en un rango amplio de velocidades de viento y, debido a la geometría angulosa de la sección del seguidor, es inevitable, por lo que deberá tenerse en cuenta la fatiga de la sección del tubo de torsión ante estas cargas oscilatorias.
Corresponde al área de la aeroelasticidad definir la amplitud y frecuencia de estas oscilaciones para cada velocidad de viento e inclinación de la sección para garantizar la fiabilidad del seguidor ante dichas cargas.
El número de Strouhal (St) describe la frecuencia a la que los vórtices se desprenden de un cuerpo de forma oscilatoria, de acuerdo con la formula:
St = \Large \frac {f L} {U}
Donde:
- St: número de Strouhal
- f: frecuencia de desprendimiento de vórtices
- L: longitud característica
- U: velocidad del fluido
Vincenc Strouhal (Čeněk Strouhal)
(Seč, 1850 – Praga, 1922)
Físico checo especializado en la física experimental. En 1878, mientras trabajaba con cables que experimentaban desprendimiento de vórtices y tonos en el viento, definió el número de Strouhal (St) que describe los mecanismos de flujo oscilante para la dinámica de fluidos.

Aunque hay bastantes estudios para formas cilíndricas, sobre todo para el diseño de chimeneas, donde se relaciona el número de Strouhal con el número de Reynolds para conocer como varía el desprendimiento de vórtices con respecto a la velocidad del fluido, no es así con otras superficies como puede ser una placa plana en semejanza con la sección de un seguidor. Por lo tanto, las frecuencias de desprendimiento deben estudiarse para cada velocidad de viento y para cada inclinación del seguidor para saber si el seguidor entra en resonancia.
A efectos prácticos, el desprendimiento vórtices en seguidores solares se puede considerar como un momento oscilatorio que es soportado por cada brazo o tubo de torsión a cada lado del mecanismo más un momento estático. Este momento oscilatorio provocará un giro de las secciones del seguidor cuya mayor amplitud se observará en la ultima sección y unas tensiones tangenciales en la sección del tubo de torsión más cercana al mecanismo para soportar dichas cargas.
De esta forma podemos expresar la carga externa del seguidor como:
M(t) = M_d sen(\omega t) + M_{est}
Donde \omega = 2 \pi f , con f definida en el número de Strouhal.
Por tanto, podemos escribir la ecuación diferencial que define el movimiento del seguidor como:
\normalsize I \ddot \theta + 2 I \omega_n \xi \dot \theta + k \theta = M(t) = M_d sen(\omega t) + M_{est}
La respuesta completa del sistema ante estas cargas con unas condiciones iniciales nulas es la siguiente:
\normalsize \theta (t) = e^{-\xi \omega_n t} \left[A \cos(\omega_d t) + B sin(\omega_d t)\right] + X sen(\omega t + \phi) + \Large \frac {M_{est}}{k}
Donde:
\normalsize X = \Large \frac{M_d/k} {\sqrt{(1-\tau^2)^2 + (2 \xi \tau)^2}}
\phi = \Large \frac{2 \xi \tau} {\sqrt{1-\tau^2}}
A = X sen \phi + \Large \frac{M_{est}} {k}
B = \Large \frac{\xi \omega_n A - X \omega cos \phi}{\omega_d}
\tau = \Large \frac{\omega}{\omega_n}
Al término:
X sen(\omega t + \phi) + \Large \frac {M_{est}}{k}
Se le denomina término permanente y es la solución de la ecuación cuando el tiempo tiende a infinito. El primer sumando corresponde a la respuesta en el régimen permanente de la carga oscilatoria, el segundo a la carga estática.
En contra, al término:
e^{-\xi \omega_n t} \left[A \cos(\omega_d t) + B sin(\omega_d t)\right]
Se le llama término transitorio y marca el camino de la solución hasta llegar al permanente.
Mostramos algunos ejemplos de respuestas para visualizar el término transitorio y permanente
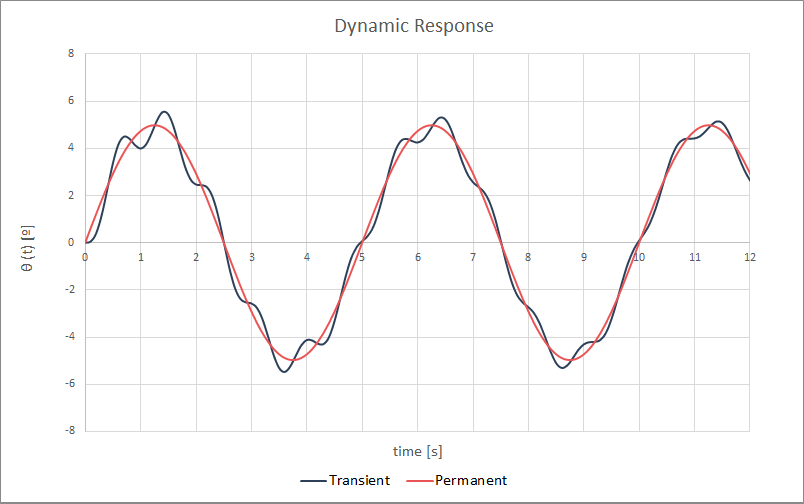
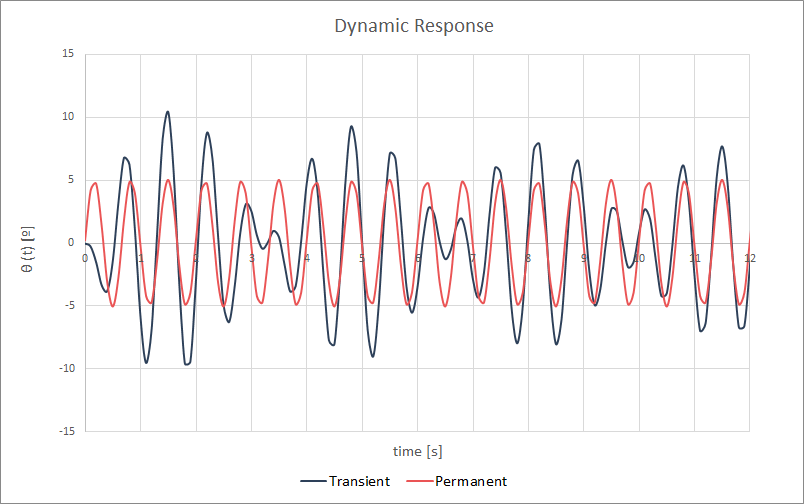
Un seguidor con un momento oscilatorio incidente, inducido por el desprendimiento de vórtices en su superficie de sotavento, siempre tenderá también a una respuesta oscilatoria con la misma frecuencia que la carga que lo excita, pero con un desfase, y cuya amplitud depende del amortiguamiento del seguidor.
Por otro lado, si consideramos una carga estática, la respuesta del seguidor tenderá también a una constante que, esta vez, depende de la rigidez del sistema.

Se le llama resonancia al fenómeno de vibración de un cuerpo a la misma frecuencia de la fuerza que lo excita. Cuando esto ocurre la amplitud de la vibración son las más grandes posibles y solo pueden atenuarse si existe un amortiguamiento efectivo.
Un seguidor solar de un eje, como cualquier estructura, tiene varias frecuencias y modos de vibración asociado. Si consideramos que este seguidor tiene dos filas de 15 módulos por cada tubo de torsión, con dicho tubo de torsión de 17.3m de longitud y #140.5mm de sección, la primera frecuencia de vibración que encontramos es de 1.2Hz. Su modo de vibración asociado es una torsión a lo largo del eje del seguidor donde el mayor giro de la sección se encuentra en la sección más alejada del mecanismo (última sección).
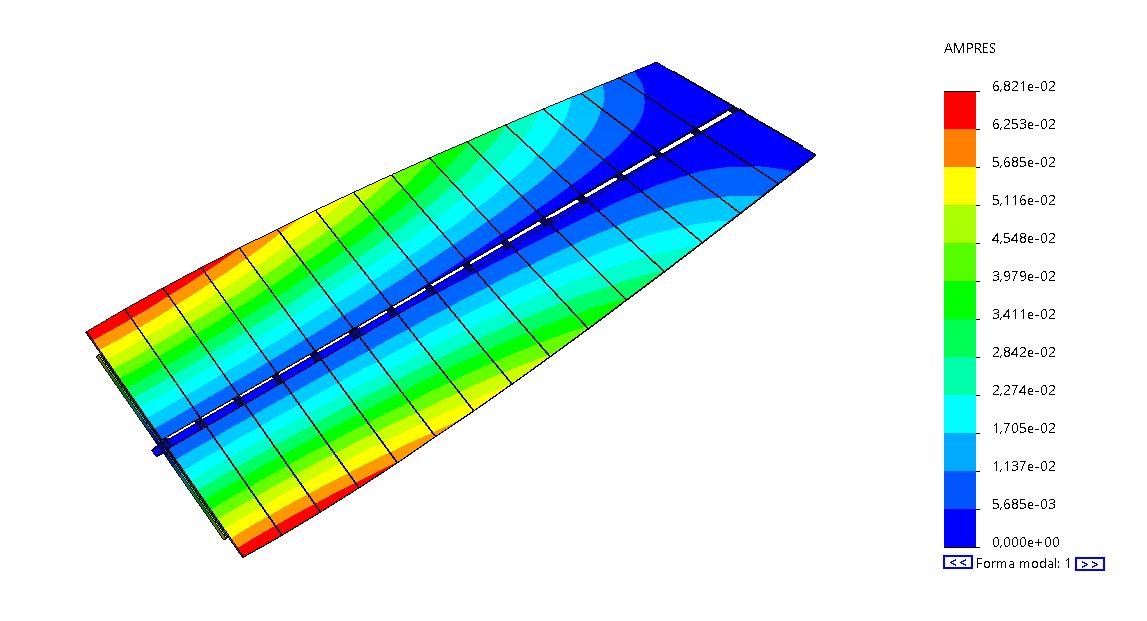
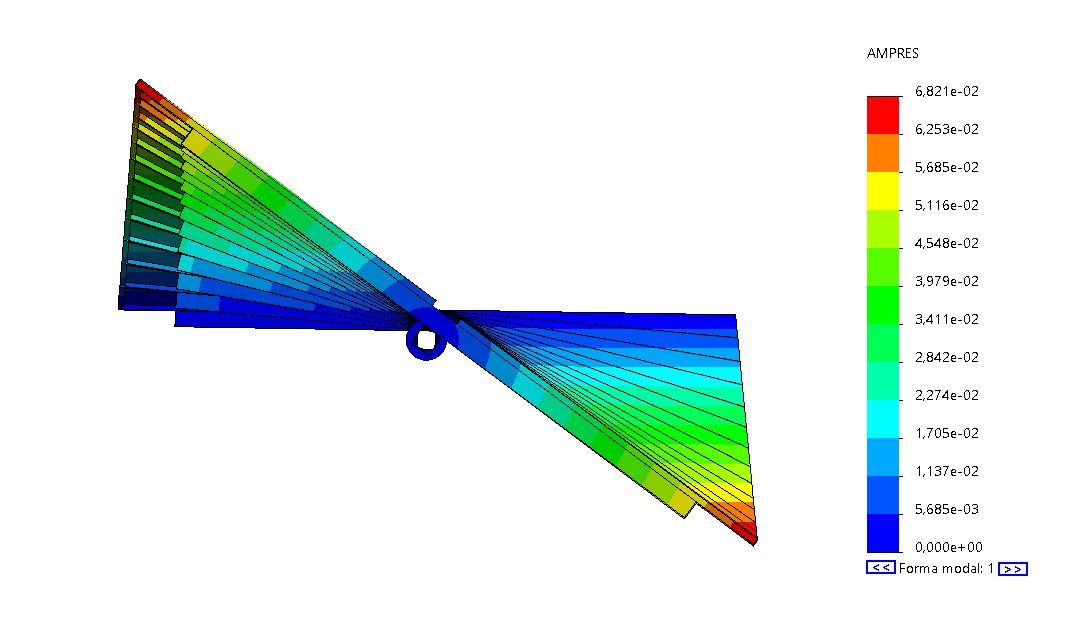
Para simplificar, ajustaremos el modelo tridimensional a uno bidimensional con una inercia equivalente (I) y una rigidez equivalente (k) que proporcionen las mismas deformaciones que la última sección en un modelo tridimensional para el mismo estado de cargas equivalentes. A efectos prácticos, asumiremos que todo el seguidor se deforma y sufre los momentos de la sección más alejada del mecanismo. Esta hipótesis está por el lado de la seguridad.
Si consideramos un seguidor cuyo tubo de torsión tiene sección cuadrada de 140mm de lado y 5mm de espesor (#140.5) en acero de construcción S355JR, el límite elástico del material se alcanza por medio de tensiones tangenciales para combinaciones de amplitud y frecuencia de momentos oscilantes.
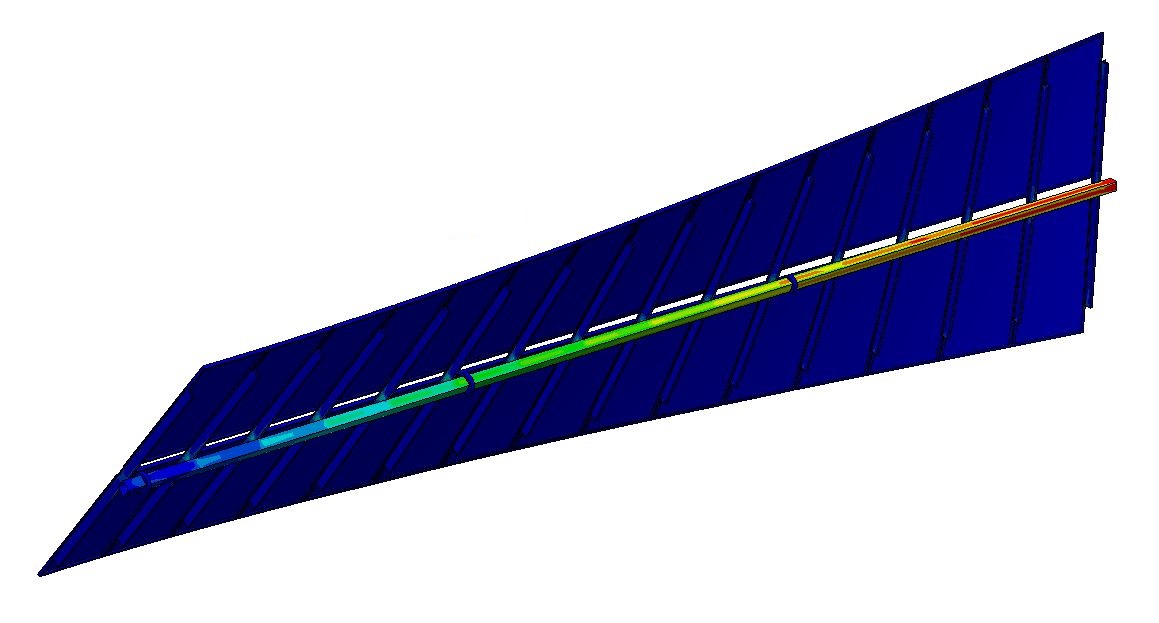
La respuesta del sistema es muy variada dependiendo de la cercanía de la frecuencia de excitación a la frecuencia natural y de su amortiguamiento.
De forma cualitativa influyen 3 parámetros principalmente:
La siguiente grafica muestra los momentos oscilantes permitidos en el límite elástico de un tubo de torsión #140.5mm de acero S355JR para diferentes valores de amortiguamiento (ξ). El seguidor porta en cada tubo de torsión 30 módulos fotovoltaicos dispuestos en dos filas de 15, con una longitud de 17.3m, una sección de 4.7m y una frecuencia natural de 1.2Hz.
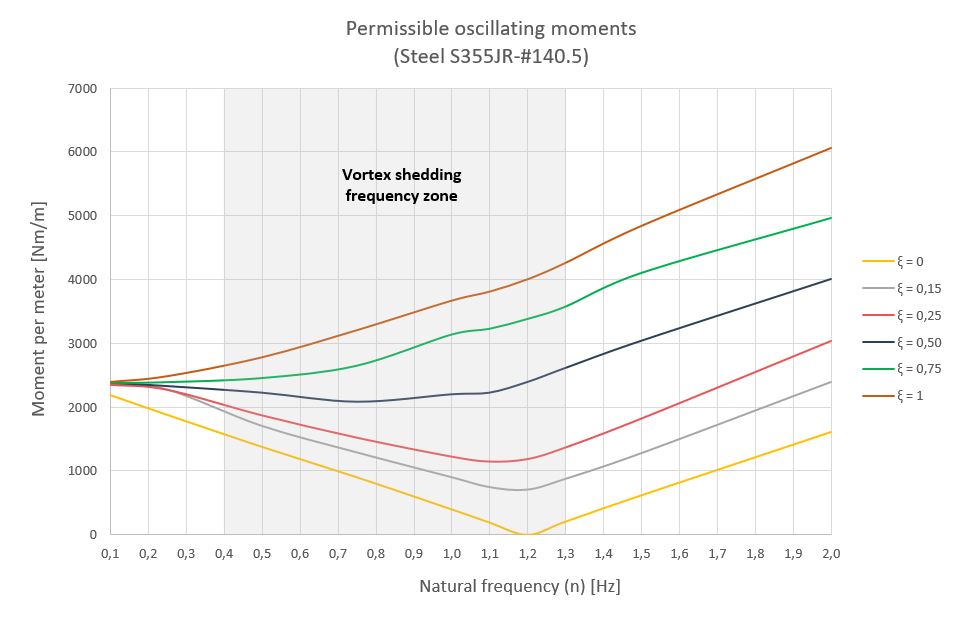
En este apartado, solo estamos contabilizando las tensiones tangenciales debidas a la torsión ( \tau_t ). Las tensiones normales debidas a los momentos de flexión ( \sigma_b ) y las tangenciales debidas al cortante ( \tau_c ) producidas por las cargas de viento de resistencia y sustentación deben ser tenidas en cuenta de acuerdo a la tensión de Von Mises ( \sigma_{VM} ) para contabilizar la tensión global sobre el tubo de torsión.
\sigma_{VM} = \sqrt{\sigma_b^2 + 3 (\tau_t + \tau_c)^2}
La velocidad de abatimiento ( U_{stow,3s,10m} ) en plantas fotovoltaicas suele estar entre 15 y 20 m/s dependiendo del emplazamiento. El desprendimiento de vórtices debe ser estudiado para todas las posiciones del seguidor por debajo de esta velocidad. Además, para la posición de abatimiento elegida y hasta la velocidad de supervivencia de la planta, las tensiones alcanzadas en el tubo de torsión debidas a este fenómeno deben estar por debajo del límite elástico del material que lo compone.
Es importante resaltar que, para velocidades de viento cercanas a la velocidad de supervivencia de la planta, ligeras inclinaciones del seguidor en la posición de abatimiento para mejorar los efectos del galope, pueden influir negativamente en el fenómeno de desprendimiento de vórtices en seguidores solares. Si bien a altas velocidades de vientos, las frecuencias de desprendimientos en seguidores solares suelen ser bajas y menores que la frecuencia natural del sistema, las amplitudes debidas a la alta velocidad de viento no lo son, ya que son directamente proporcionales al cuadrado de dicha velocidad, por lo que pueden ocasionar tensiones importantes en el tubo de torsión.
Por esta cuestión, para la posición de abatimiento, el amortiguamiento debe ser elegido tanto para asegurar que la velocidad crítica de galope está por encima de la velocidad de supervivencia de la planta, como para asegurar que las vibraciones producidas por el desprendimiento de vórtices no proporcionan tensiones que sobrepasen el límite elástico del tubo de torsión antes de alcanzar la velocidad de supervivencia.
Hemos definido la respuesta del sistema ante momentos oscilatorios inducidos por el desprendimiento de vórtices en seguidores solares sobre sus superficies a sotavento. El siguiente paso es determinar el valor de la amplitud y frecuencia de estos momentos para una velocidad de viento determinada junto con una inclinación del seguidor concreta, ya que esta frecuencia y amplitud cambiarán debido a estos dos factores.
La frecuencia natural del sistema (n) dada por su rigidez (k) así como el coeficiente de amortiguamiento (ξ) juegan un papel muy importante, ya que el seguidor girará lo que le permita su rigidez, junto con lo que le permita girar el amortiguamiento en velocidad, obteniéndose momentos variables dependientes de estos dos valores.
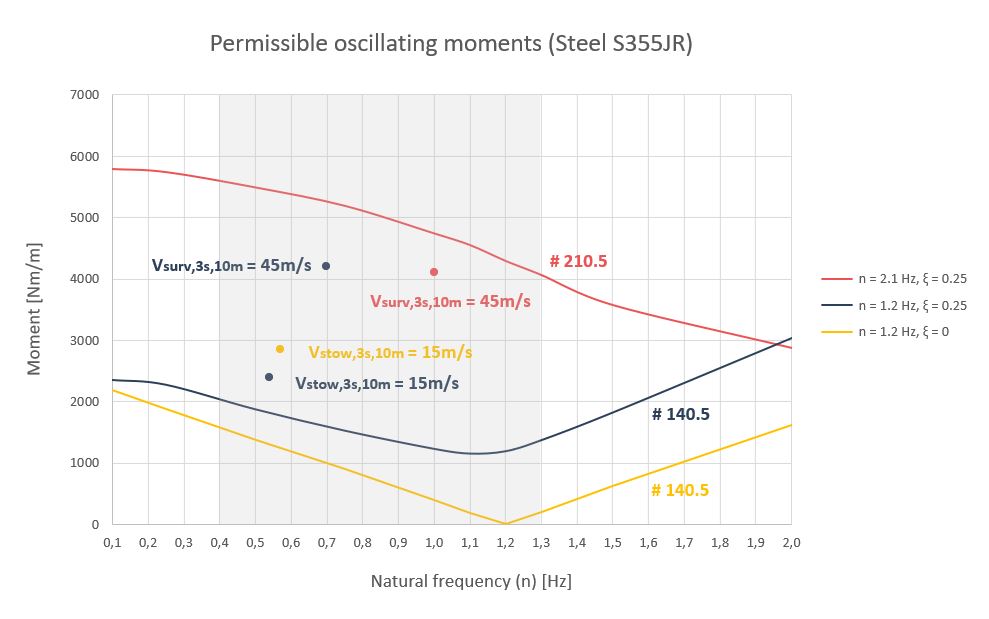
Un seguidor con una frecuencia natural de 1.2Hz sin amortiguamiento físico como tal no puede soportar los momentos oscilantes debidos al viento que proporciona la velocidad de supervivencia de la planta ( U_{surv,3s,10m} \small \approx 45m/s ), ya que generará deformaciones con amplitudes demasiado altas que proporcionarán tensiones tangenciales en el tubo de torsión que sobrepasen su límite elástico mucho antes de alcanzar dicha velocidad. De hecho, no lo hará para ningún amortiguamiento posible. Para ello, sería necesario modificar la rigidez del sistema aumentando la sección del tubo de torsión a #210.5 subiendo, de esta forma, la frecuencia natural del sistema (n) a 2.1Hz.
Respuesta a cualquier función
Cualquier fuerza exterior que afecte al seguidor puede ser representada por una función en el tiempo que puede aproximarse mediante la suma de una serie de escalones M(\tau) de duración finita \Delta \tau , cada uno de los cuales produce una impulso de M(\tau) \Delta \tau.
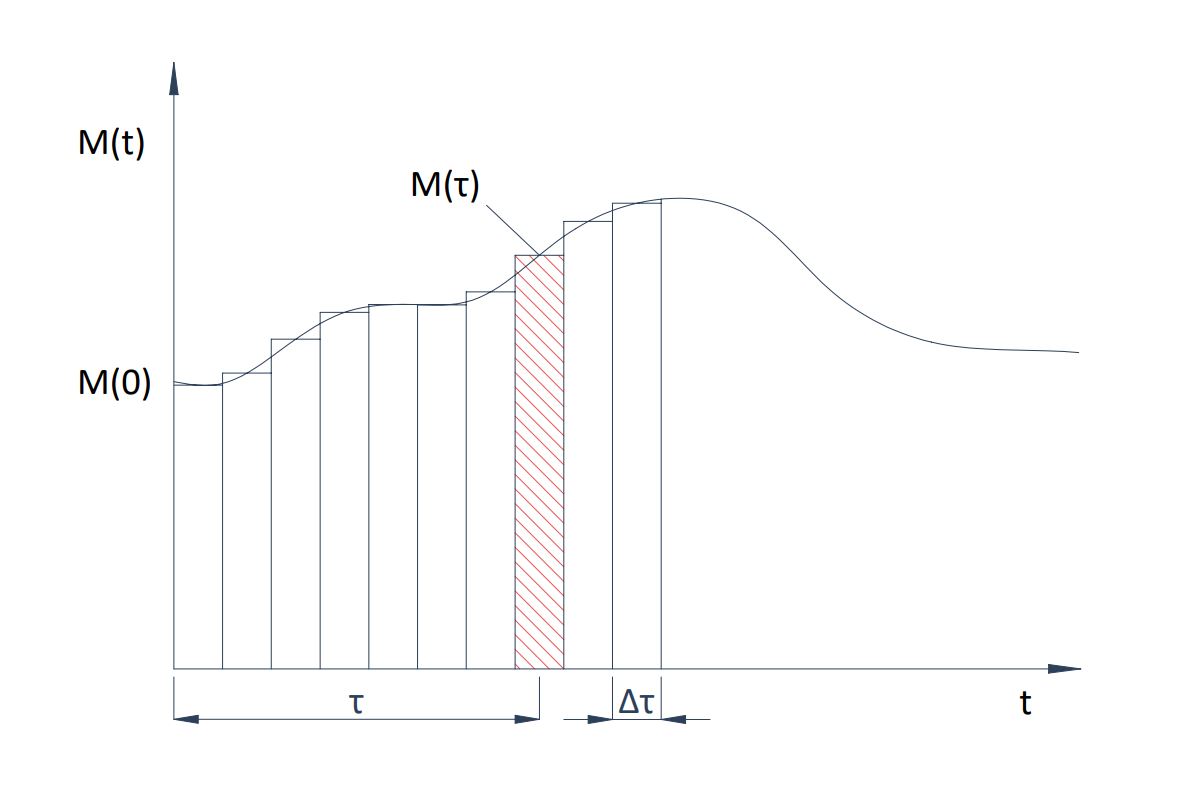
Esta aproximación puede expresarse de la forma:
M(t) = \sum_{i=1}^n M(\tau_i)
Teniendo un valor constante M(\tau_i) en cada intervalo comprendido entre \tau_i - \large \frac{\Delta \tau}{2} y \tau_i + \large \frac{\Delta \tau}{2} (igual al valor de la función en el punto ) y siendo nula en el resto del tiempo.
Si los valores de \Delta \tau se hacen tender a cero, \Delta \tau \rightarrow d\tau, los impulsos tendrán un valor M(\tau) d\tau. En este caso, la aproximación mediante una suma de infinitos impulsos se hace exacta. El valor de la respuesta a cada uno de los impulsos en que se ha dividido la función, para condiciones iniciales nulas, puede expresarse como:
d\theta(t) = M(\tau) h(t-\tau) d\tau
Donde d\theta(t) representa el aumento del valor de la respuesta debido al impulso diferencial M(\tau) d\tau, y h(t-\tau) es el valor de la respuesta a un impulso unidad producido en el instante \tau (con condiciones iniciales nulas).
Así, aplicando el principio de superposición, con condiciones iniciales nulas, la respuesta en cualquier instante t, será:
\theta(t) = \large \int_0^t \normalsize M(\tau) h(t-\tau) d\tau
Expresión que se denomina integral de Duhamel.
Jean-Marie Constante Duhamel
(Saint-Malo, 1797 – París, 1872)
Matemático y físico francés que realizó notables contribuciones al cálculo infinitesimal. El teorema de Duhamel aplicado al cálculo infinitesimal afirma que la suma de una serie de infinitesimales se mantiene cuando son reemplazados por su parte principal.

La función h(t-\tau), respuesta al impulso en el instante t-\tau, se puede expresar mediante:
h(t-\tau) = \Large \frac{e^{-\xi \omega_n (t-\tau)}}{I\omega_d} \normalsize \sin \left[ \omega_d(t-\tau)\right]
De acuerdo con estas expresiones y teniendo en cuenta condiciones iniciales nulas, la respuesta en el tiempo de un sistema de un grado de libertad, forzado a cualquier función M(t), puede obtenerse mediante la ecuación:
\theta(t) = \large \int_0^t \normalsize M(\tau) \Large \frac{e^{-\xi \omega_n (t-\tau)}}{I\omega_d} \normalsize \sin \left[ \omega_d(t-\tau)\right] d\tau
Teniendo en cuenta que se integra sobre \tau, por lo que t es constante, y considerando el seno de ángulos que se restan, tenemos que:
\theta(t) = \Large \frac{e^{-\xi \omega_n t}}{I\omega_d} \normalsize \left[ C1 \sin(\omega_dt) - C2 \cos(\omega_dt)\right]
Donde:
C1 = \large \int_0^t \normalsize M(\tau) e^{ \xi \omega_n \tau} \cos( \omega_d\tau) d\tau
C2 = \large \int_0^t \normalsize M(\tau) e^{ \xi \omega_n \tau} \sin( \omega_d\tau) d\tau
Derivando la expresión anterior con respecto al tiempo (t) se obtiene la expresión de la velocidad de la vibración del seguidor:
\dot \theta(t) = \Large \frac{d\theta(t)}{dt} \normalsize = \Large \frac{e^{-\xi \omega_n t}}{I\omega_d} \normalsize (A1 + A2 )
Con A1 y A2 como:
A1 = C1 \left[ -\xi \omega_n \sin(\omega_dt) + \omega_d \cos(\omega_dt)\right]
A2 = C2 \left[ \xi \omega_n \cos(\omega_dt) + \omega_d \sin(\omega_dt)\right]
Estas dos integrales, C1 y C2, se pueden aproximar a través de cualquier método de numérico de integración. Para la regla del trapecio tenemos que:
\large \int_a^b \normalsize f(x) dx \approx \Large \frac{b-a}{2} \normalsize \left[ f(a) + f(b) \right]
Y dado que un programa computacional divide el tiempo en intervalos muy pequeños y calcula una solución a cada intervalo, podemos aproximar las integrales de la siguiente forma:
\small C1(t) \approx C1(t-1) + \normalsize \frac{\Delta t}{2} \small \left[ M(t) e^{ \xi \omega_n t}\cos(\omega_dt) + M(t-1) e^{ \xi \omega_n (t-1)}\cos(\omega_d(t-1)) \right]
\small C2(t) \approx C2(t-1) + \normalsize \frac{\Delta t}{2} \small \left[ M(t) e^{ \xi \omega_n t}\sin(\omega_dt) + M(t-1) e^{ \xi \omega_n (t-1)}\sin(\omega_d(t-1)) \right]
Desprendimiento de vortices + Galope/Divergencia
Debido principalmente a la forma angulosa de la sección del seguidor, el desprendimiento de vórtices estará presente en plantas solares, siempre y cuando el viento sople con una velocidad considerable, por lo tanto, se deberá diseñar la rigidez (k) y el amortiguamiento (ξ) del sistema para minimizar las tensiones tangenciales en el tubo de torsión.
El galope y la divergencia aparecen a una velocidad de viento puntual y determinada. Si se dimensionan bien los valores de rigidez y amortiguamiento del seguidor, estos dos fenómenos aparecerán más allá de la velocidad de supervivencia de la planta por lo que no se deberán considerar junto con el desprendimiento de vórtices, ya que serían fenómenos independientes y nunca aparecerían a la vez.
En el caso de que se diera esta situación, galope o divergencia proporcionan inestabilidades mucho más fuertes que el desprendimiento de vórtices en seguidores solares, solo comparable a este último si la separación de vórtices ocurriera en resonancia ( \omega = \omega_n ) con amortiguamiento nulo ( \xi \approx 0 ). Por lo que se considera fallo catastrófico en un seguidor si: