Diseño aeroelástico de seguidores
En este post analizaremos los parámetros que intervienen en el diseño aeroelástico de seguidores. Para ello se estudiará un seguidor tipo con 30 módulos fotovoltaicos a cada lado del mecanismo dispuestos en 2 filas y con una longitud de 17.3 metros por brazo (35 metros totales de seguidor), no presente inestabilidades aeroelásticas para las diferentes velocidades de viento que pueden darse en una planta fotovoltaica.
Los seguidores de un eje con una sola fila de módulos son muchísimo más estables ya que tienen una longitud de la sección (b) de alrededor de 2.5m (el largo del módulo). Incrementar este parámetro influye negativamente sobre la estabilidad del seguidor si estamos estudiando su comportamiento aeroelástico. Como ejemplo, los momentos obtenidos actúan con el cuadrado de este parámetro y el galope lo hace con el cubo.
El mercado solar está tendiendo a una configuración de doble fila, pero si se viene de la instalación de seguidores con una única fila de módulos, habrá que hacer las modificaciones necesarias para evitar fenómenos aeroelásticos debido al aumento del ancho de la sección.
Geometría del seguidor
Analizaremos un seguidor solar de un eje que porta 30 módulos dispuestos en dos filas por cada tubo de torsión (60 módulos totales por seguidor) a cada lado del mecanismo central. Las filas están separadas por una distancia de 140mm.
Las dimensiones del modulo que se han tenido en cuenta son 1130 x 2250 mm, por lo que la superficie a cada lado del mecanismo es de 17.3 x 4,7 m.
El tubo de torsión tiene una sección cuadrada de pared delgada de #140.5 mm y una longitud de 17.3 m como se ha mencionado líneas anteriores. Los módulos se encuentran separados del tubo de torsión por medio de los perfiles que lo portan a una distancia de 200mm.
Velocidades de diseño
Para el diseño aeroelástico de seguidores en una planta fotovoltaica hay 2 velocidades importantes a tener en cuenta en el diseño de seguidores:
Las velocidades críticas que valoran la aparición de los fenómenos aeroelásticos gemelos (galope y divergencia) son velocidades medias o velocidades horarias ( V_{1h} ). Sin embargo, las velocidades que definen la planta son velocidades pico ( V_{3s} ) y suelen tomarse de códigos de edificación que pueden incluir, o no, un coeficiente de seguridad, usualmente alrededor de \sqrt{1.6} . La relación entre la velocidad media y el pico máximo que se alcanza con dicha velocidad media está medida probabilísticamente por medio de la siguiente gráfica, por lo que la relación entre ambas es de:
\Large \frac{V_{3s}}{V_{1h}} \normalsize = 1.52
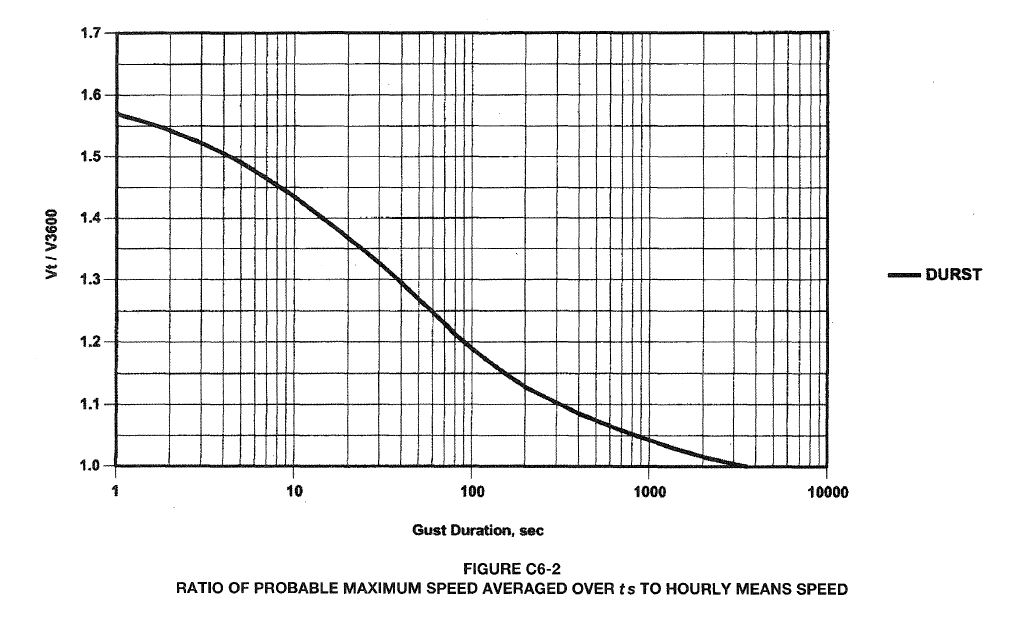
Hacemos esta distinción de velocidades porque los códigos de edificación suelen trabajar con velocidades pico ( V_{3s} ), mientras que programas de simulación y túneles de viento lo hacen con velocidades medias ( V_{1h} ). La altura de referencia para estas velocidades siempre se toma a 10 metros.
Para este análisis se tomarán las siguientes velocidades de diseño que son usuales en la mayoría de plantas solares fotovoltaicas:
| V1h [m/s] | V3s [m/s] | |
|---|---|---|
| Vsurv | 30 | 45 |
| Vstow | 10 | 15 |
Modo de vibración
En aeroelasticidad de seguidores solares es fundamental tener en cuenta la frecuencia y la forma con la que vibran ante las diferentes velocidades de viento a las que se enfrenta la planta fotovoltaica.
A partir de aquí, haremos referencia al seguidor como cada una de las partes a cada lado del mecanismo, ya que ambas se deforman independientemente.
Para la mitad del seguidor de dos filas de módulos, el primer modo de vibración torsional se produce a una frecuencia (n) de 1.2 Hz.
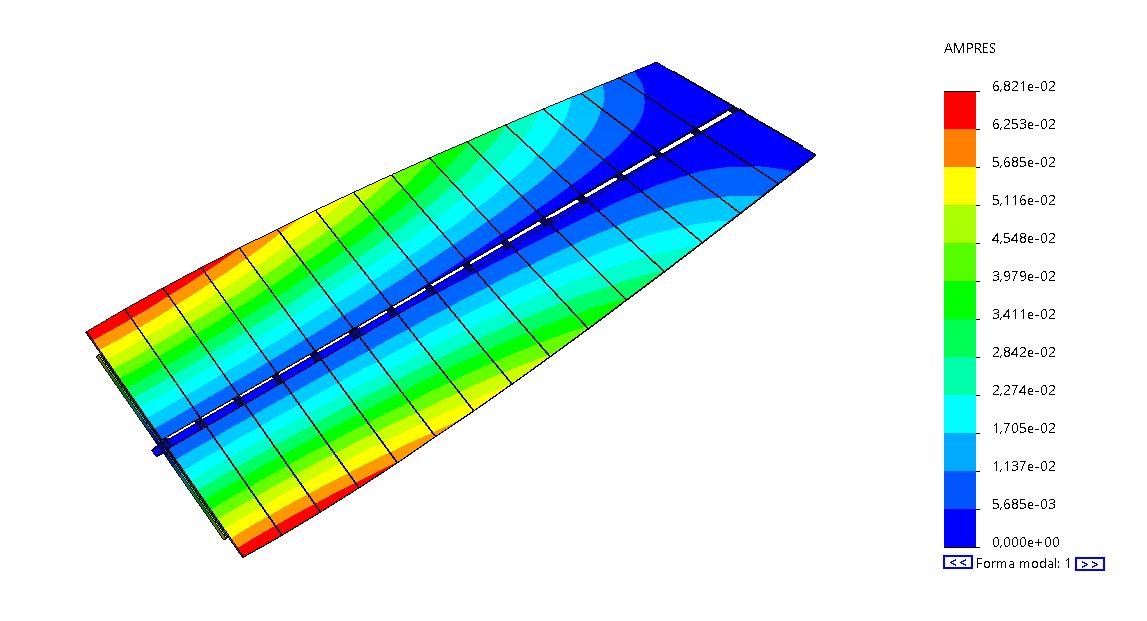
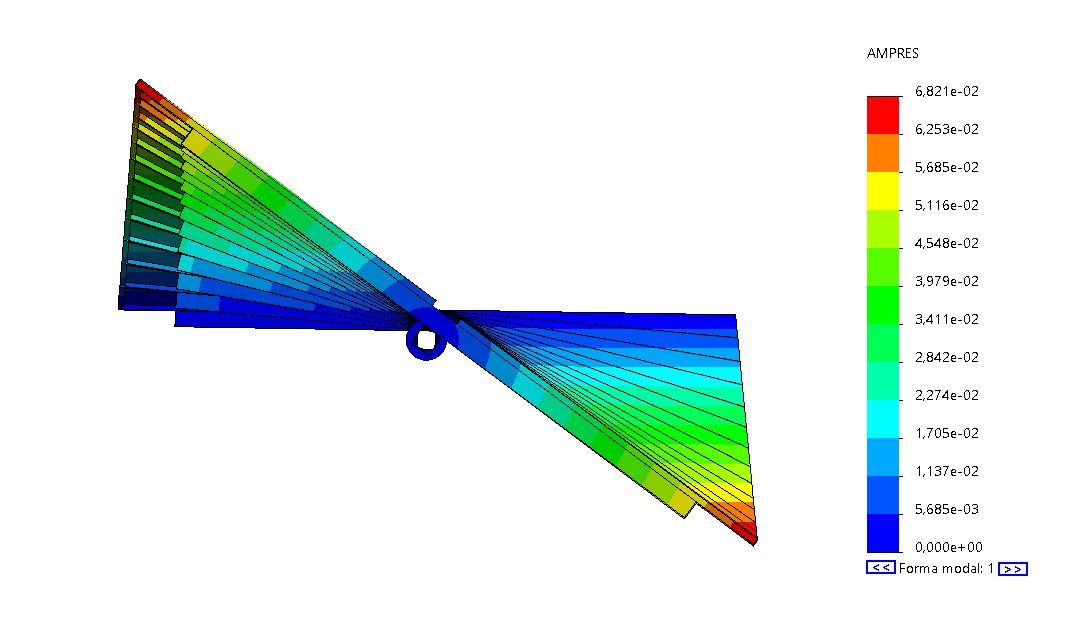
Para simplificar, ajustaremos el modelo tridimensional a uno bidimensional con una inercia equivalente (I) y una rigidez equivalente (k) que proporcionen las mismas deformaciones que la última sección en un modelo tridimensional para el mismo estado de cargas equivalentes. A efectos prácticos, asumiremos que todo el seguidor se deforma y sufre los momentos de la sección más alejada del mecanismo. Esta hipótesis está por el lado de la seguridad.
Para el seguidor descrito tenemos los siguientes valores:
- n = 1.2 Hz
- I = 105 kg/m²
- k = 5969 Nm/rad
Aeroelasticidad en seguidores
Inestabilidades gemelas
En el diseño aeroelástico de seguidores, la divergencia torsional aparece a una velocidad de viento cuyo coeficiente de momentos anula la rigidez del sistema (k). Si se reduce la carga sobre el seguidor a su centro de presiones, la velocidad crítica de aparición de la divergencia es:
U_{cr}|_{div} = \Large \sqrt {\frac {2k_{\theta}}{\rho b^2 \frac{ \partial c_m}{\partial \alpha}}}
Con:
- Ucr = 30 m/s
- b = 4.7 m
- ρ = 1.225 kg/m³
- \Large \frac{ \partial c_m}{\partial \alpha} ≈ 1.6 aproximado con el anexo del Eurocódigo.
Y despejando k, se obtiene la rigidez mínima para que no se alcance la divergencia torsional antes de la velocidad de supervivencia:
k = \Large \frac {1}{2} \normalsize \rho U_{cr}^2 b^2 \Large \frac{ \partial c_m}{\partial \alpha} \normalsize = \Large \frac {1}{2} \normalsize 1.225 · 30^2 · 4.7^2 · 1.6 = 19483 Nm/rad
Ya que la rigidez del seguidor es menor que la calculada, el seguidor alcanzará la divergencia torsional a una velocidad más baja que la velocidad de supervivencia, por lo que esta situación es inadmisible.
En este caso hay que subir la rigidez del seguidor hasta, al menos, 19483 Nm/rad para que no aparezcan fenómenos aeroelásticos debidos a divergencia torsional. En un seguidor de un eje el elemento que soporta la torsión es el propio tubo de torsión, actualmente definido en #140.5mm. Para aumentar la rigidez es necesario aumentar el canto del tubo hasta 210mm, conservando el mismo espesor de pared. Para este caso se obtendría una nueva rigidez de 20559 Nm/rad, por encima de la calculada.
Esta nueva rigidez proporciona una nueva frecuencia natural del sistema (n) de 2.1Hz que influirá positivamente en las instabilidades de galope torsional y desprendimiento de vórtices.
Como puede observarse el aumento de la sección del seguidor (b) tiene que compensarse con un aumento de la rigidez para mantener al seguidor estable frente a la divergencia torsional.
U_{cr}|_{gal} = \Large \frac {4 I_{\theta} \omega_n \xi} {\rho b_c^2 r \frac{\partial c_m}{\partial \alpha}}
Con:
- I = 115 kg/m²
- n =2.1 Hz
- \omega_n = 2 \pi n
- ρ = 1.225 kg/m³
- b = 4.7 m
- r ≈ b/4
- \Large \frac{ \partial c_m}{\partial \alpha} ≈ 1.6 aproximado con el anexo del Eurocódigo.
Y despejando ξ, se obtiene el coeficiente de amortiguamiento mínimo para que no se alcance el galope torsional antes de la velocidad de supervivencia.
\xi = \Large \frac {1}{16} \frac {\rho U_{cr}^2 b^3 \frac{\partial c_m}{\partial \alpha}}{I \omega_n} \normalsize = \Large \frac {1}{16} \frac {1.225 · 30^2 · 4.7^3 · 1.6}{115 · 2\pi · 2.1} \normalsize = 0.25
Si el amortiguamiento del seguidor es igual o superior a 0.25, éste no entra en galope antes de la velocidad de supervivencia. Esto implica tener un sistema de amortiguamiento físico sobre el seguidor para alcanzar este valor, ya que por sí sola, la estructura del seguidor tiene un coeficiente de amortiguamiento muy bajo, en torno a 0.01.
Desprendimiento de vórtices
Es importante comprender que, en el diseño aeroelástico de seguidores, se deben soportar los momentos inducidos por el desprendimiento de vórtices en sotavento en cualquier posición con una velocidad de viento igual o inferior a la velocidad de abatimiento ( V_{stow,1h} \small = 10m/s ). Debido a que la energía para mover el seguidor depende del cuadrado de la velocidad, la velocidad de abatimiento marcará el peor caso posible para cada posición del seguidor.
A continuación, se exponen las vibraciones obtenidas en la última sección del seguidor para una velocidad de viento de 10m/s, para 7 inclinaciones diferentes de operación separadas 20º.
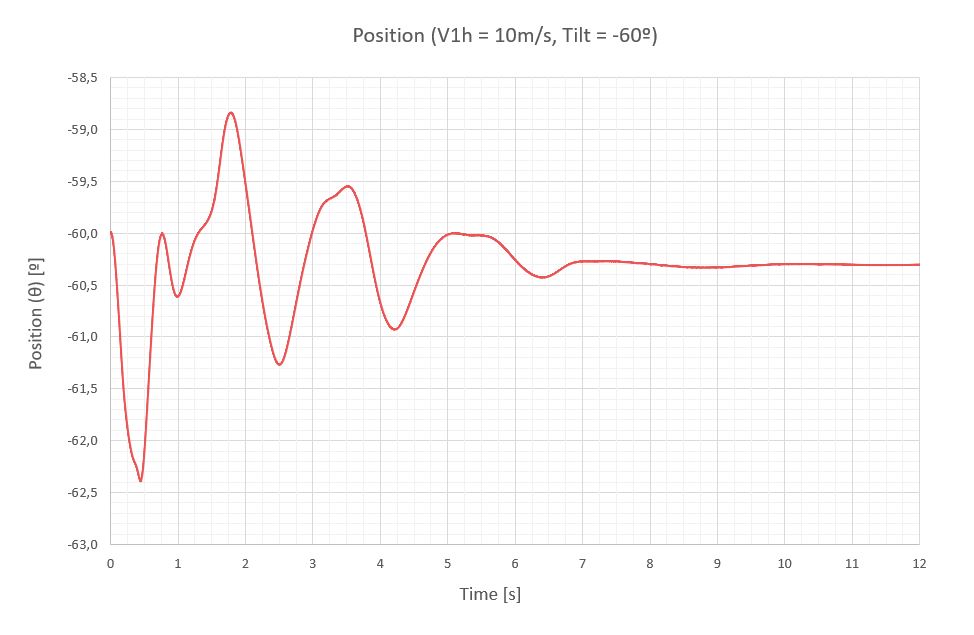
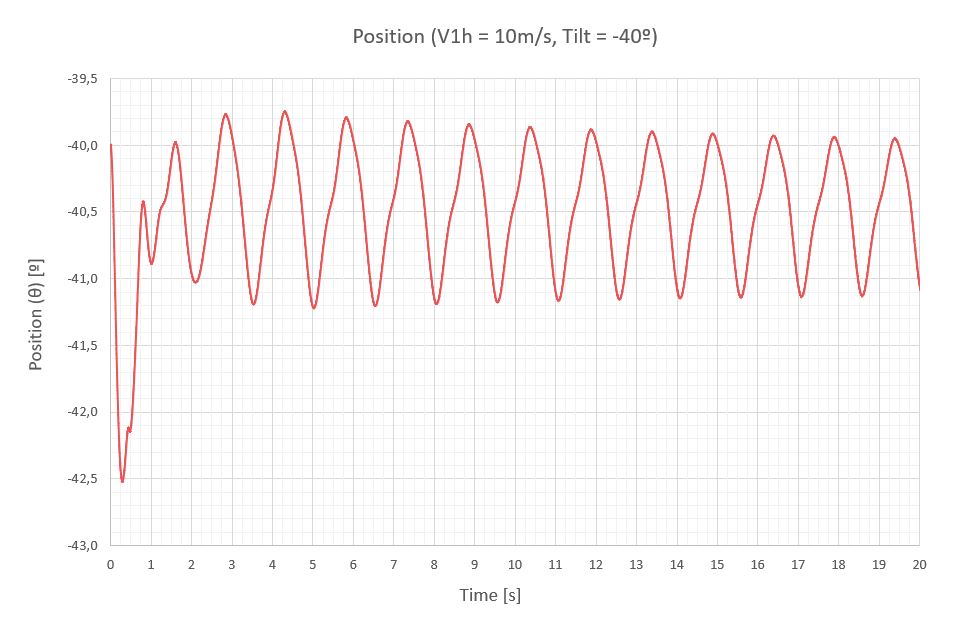
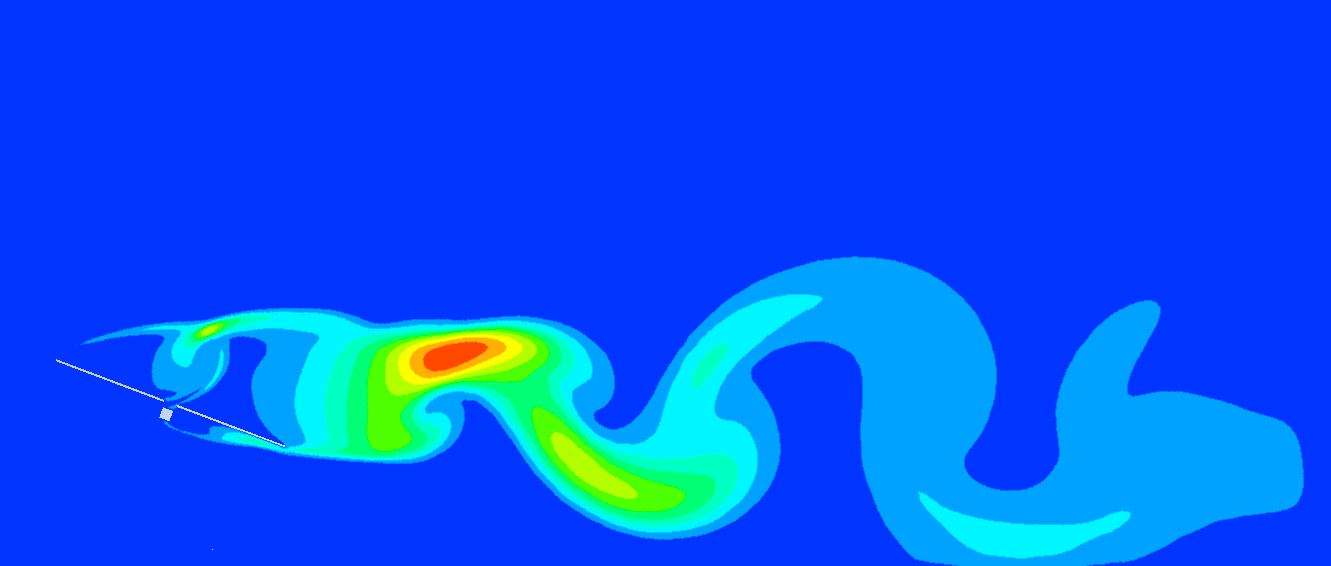
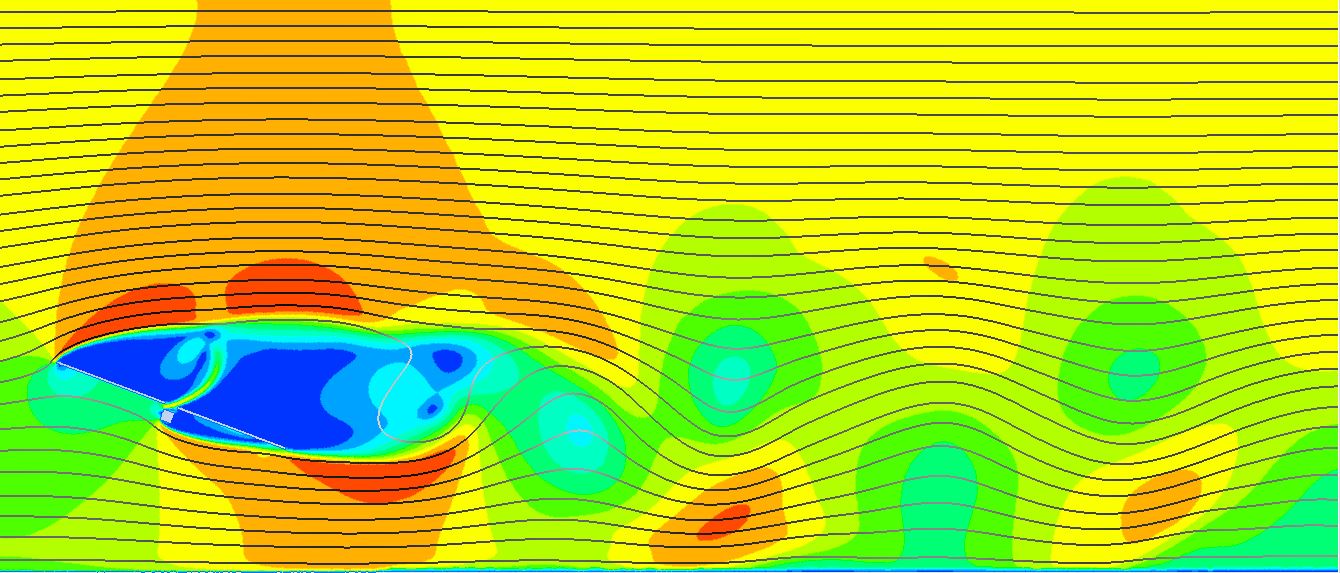
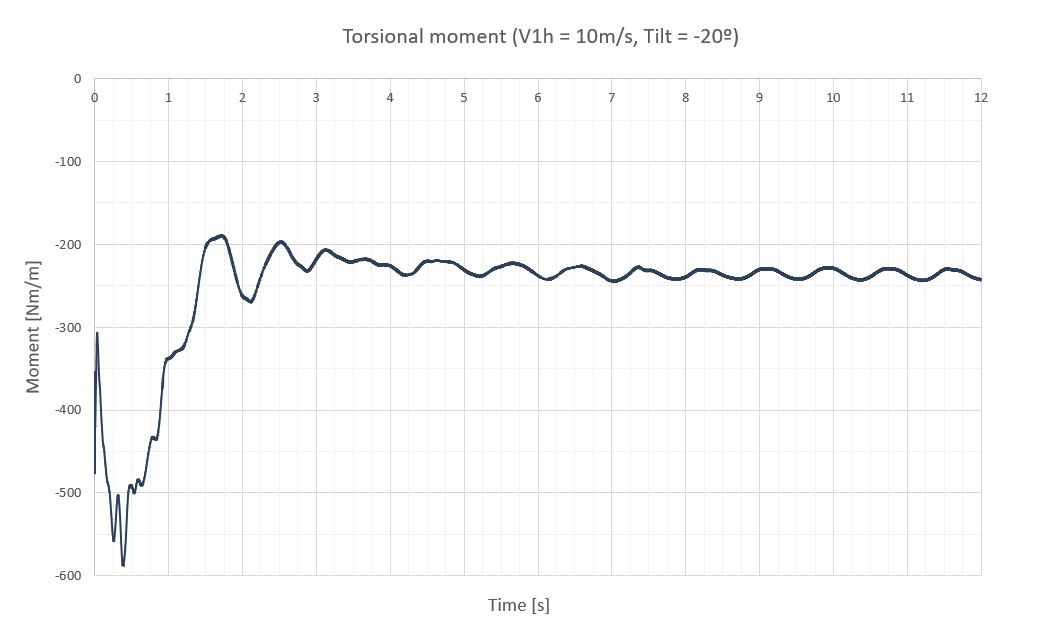
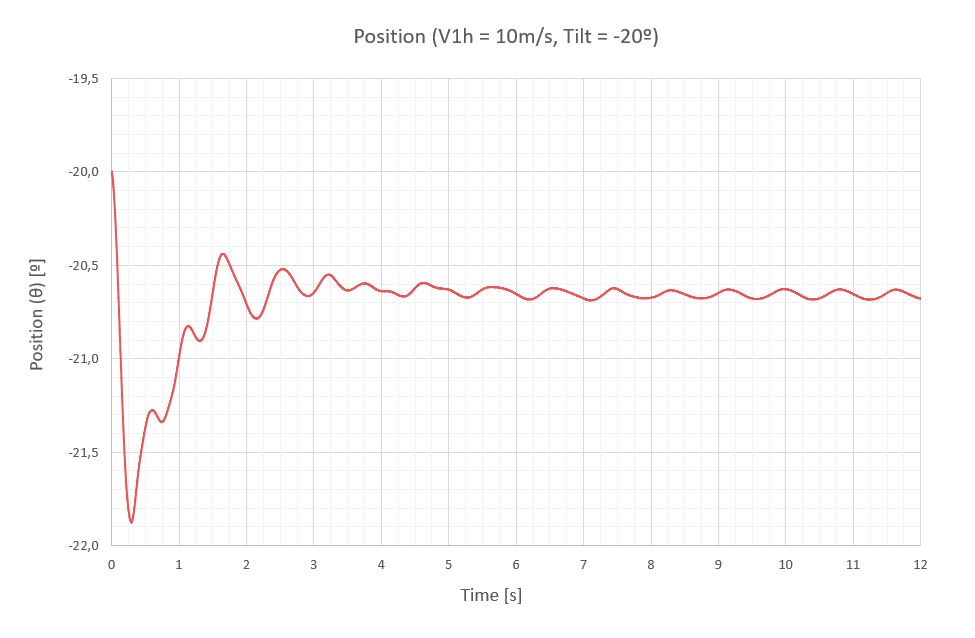
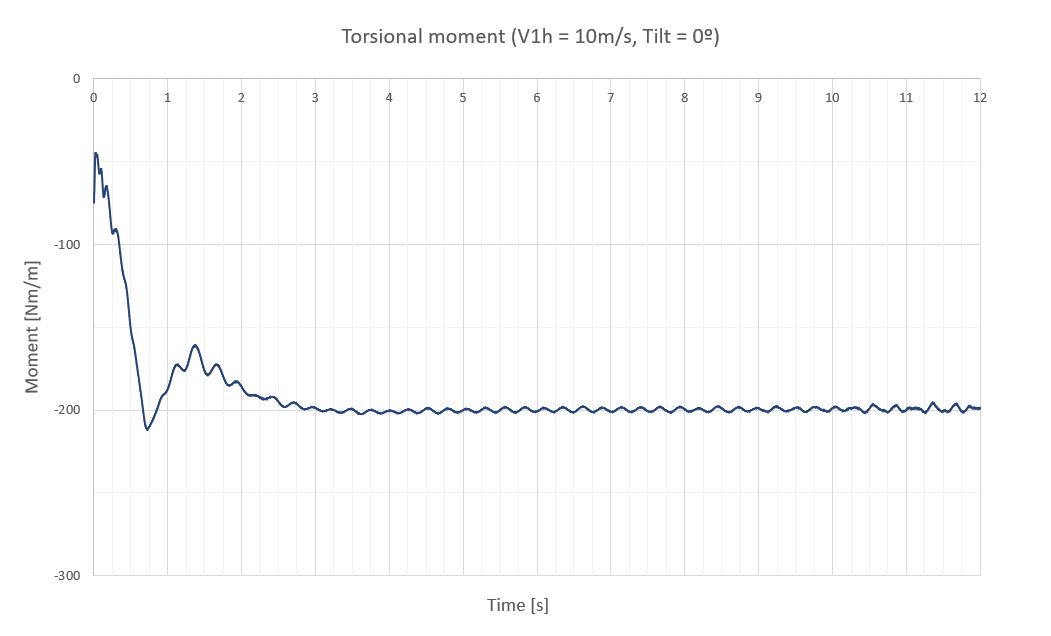
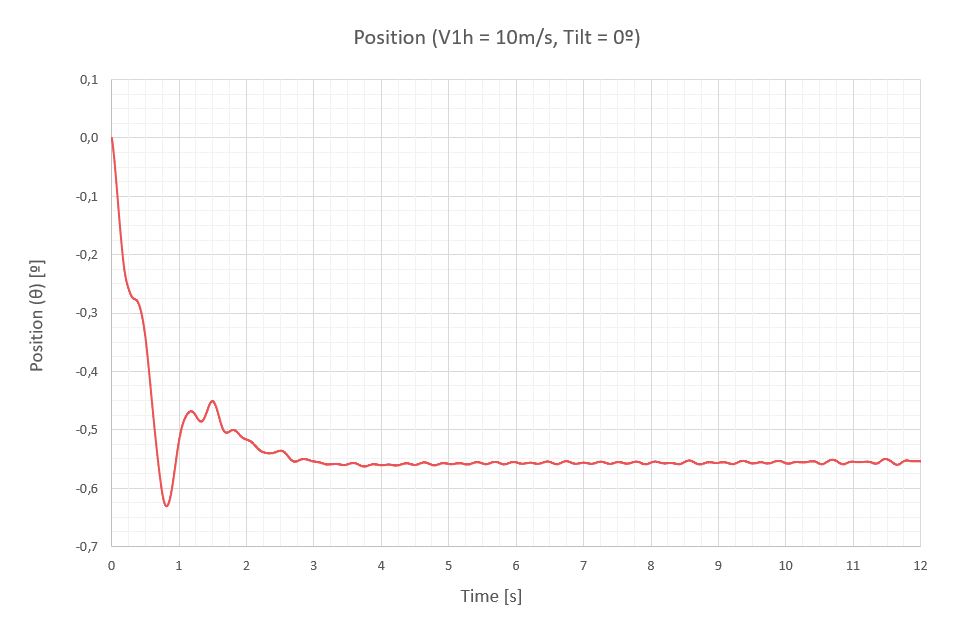
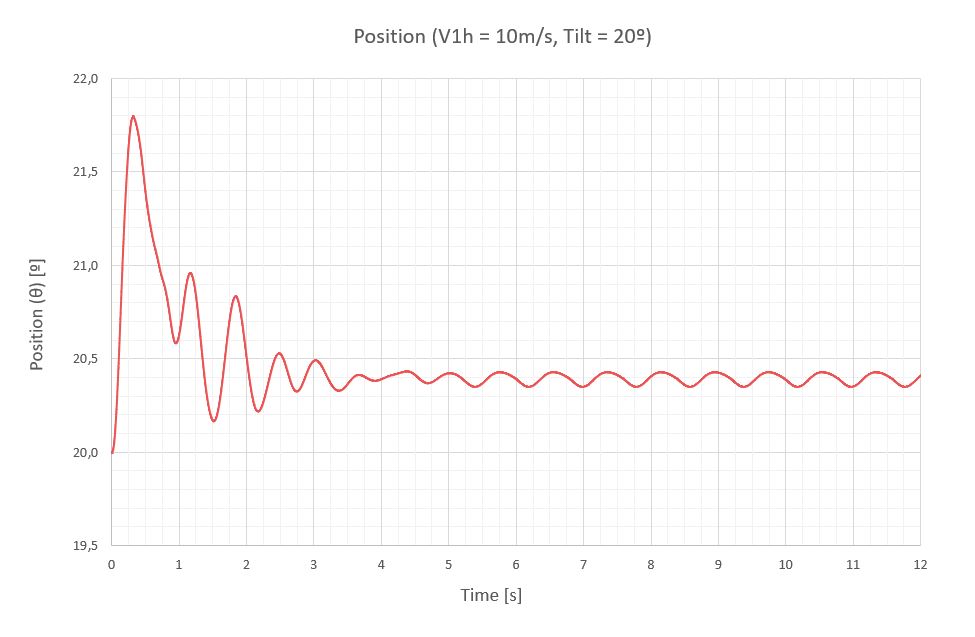
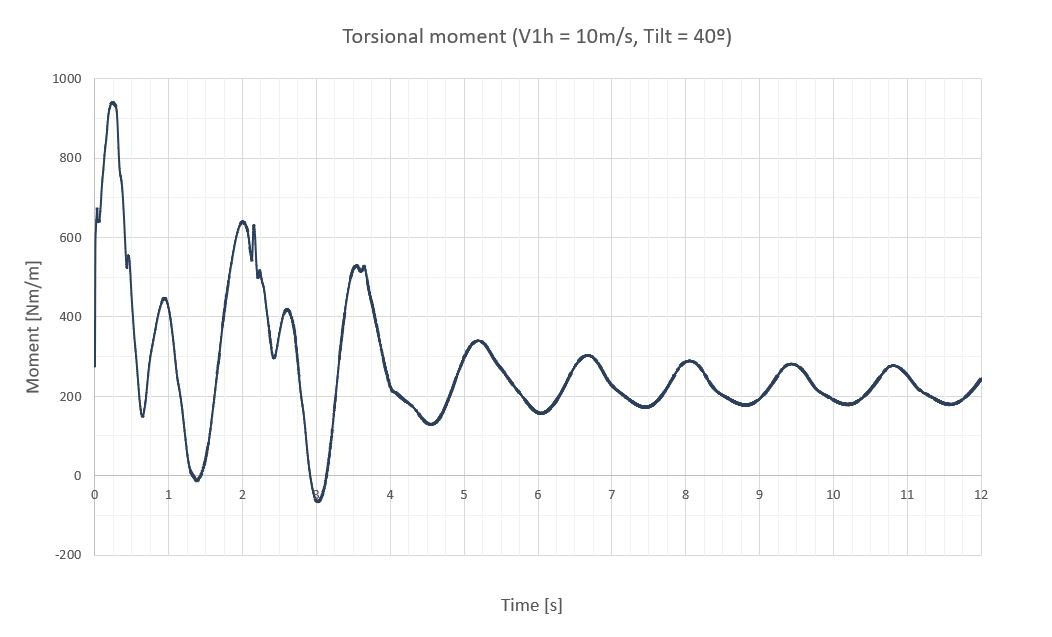
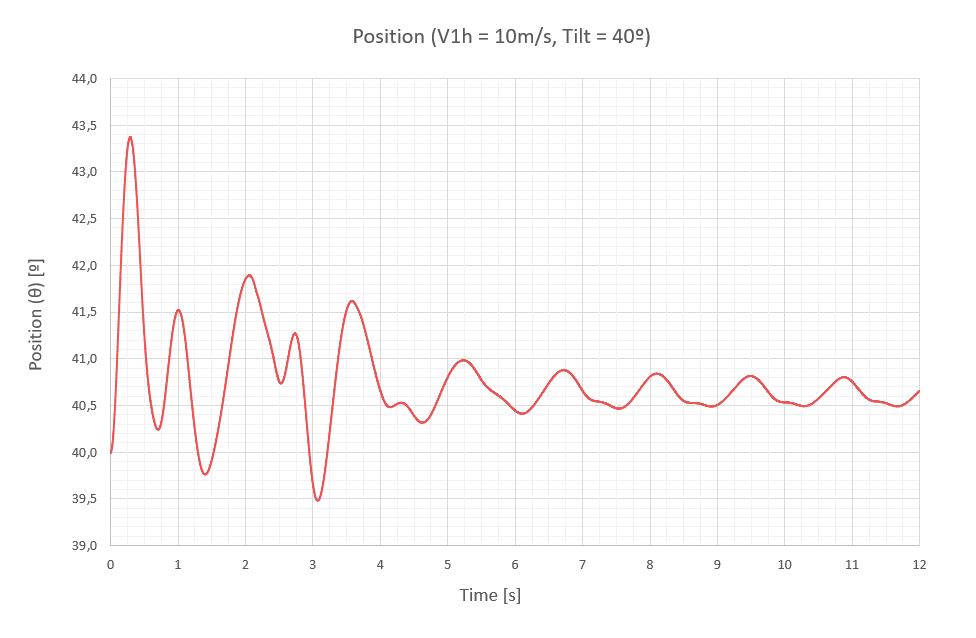
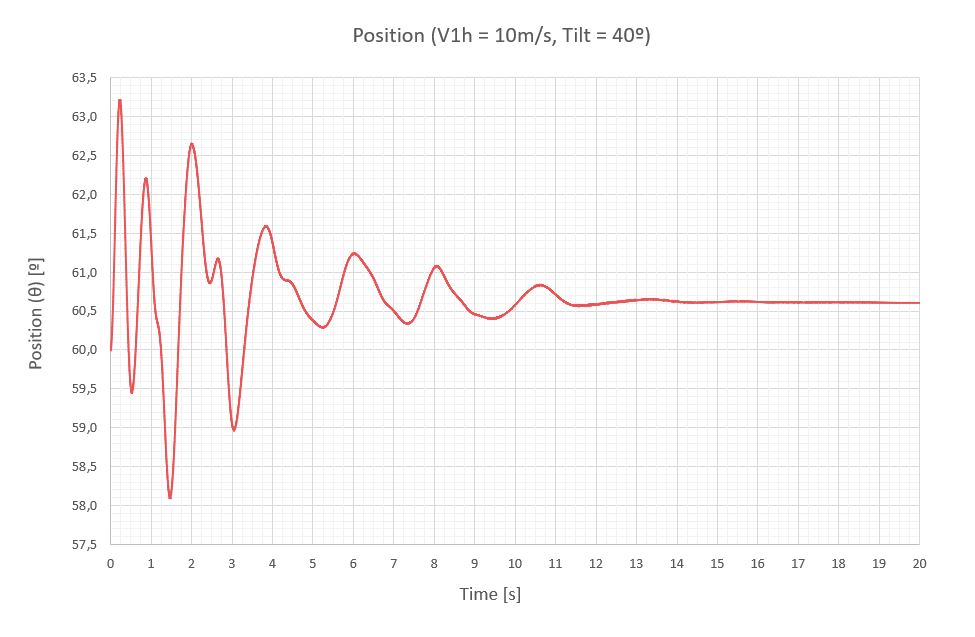
A continuación, una tabla resumen con los momentos de torsión (M) y la respuesta del seguidor a través del giro de su última sección (Δθ), que está medido con respecto a la inclinación del seguidor que le corresponde para poder compararlos.
| Tilt [º] | T [s] | f [Hz] | Mest [Nm/m] | Ma [Nm/m] | Mmax [Nm/m] | Δθest [º] | Δθa [º] | Δθmax [º] |
|---|---|---|---|---|---|---|---|---|
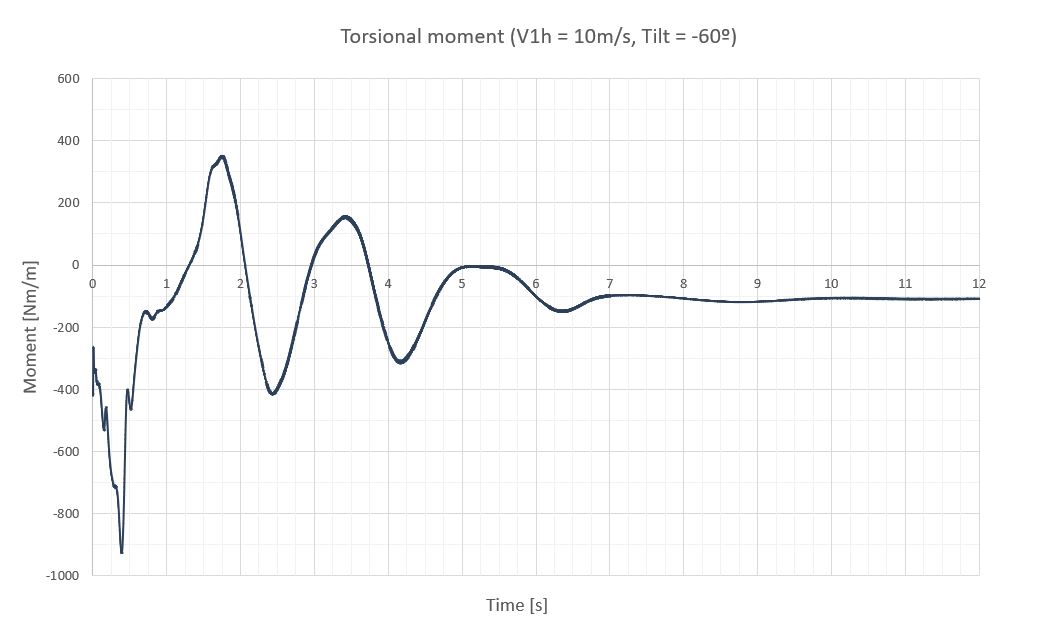
| -60 | 0 | 0 | -110 | 0 | -110 | -0.31 | 0 | -0.31 |
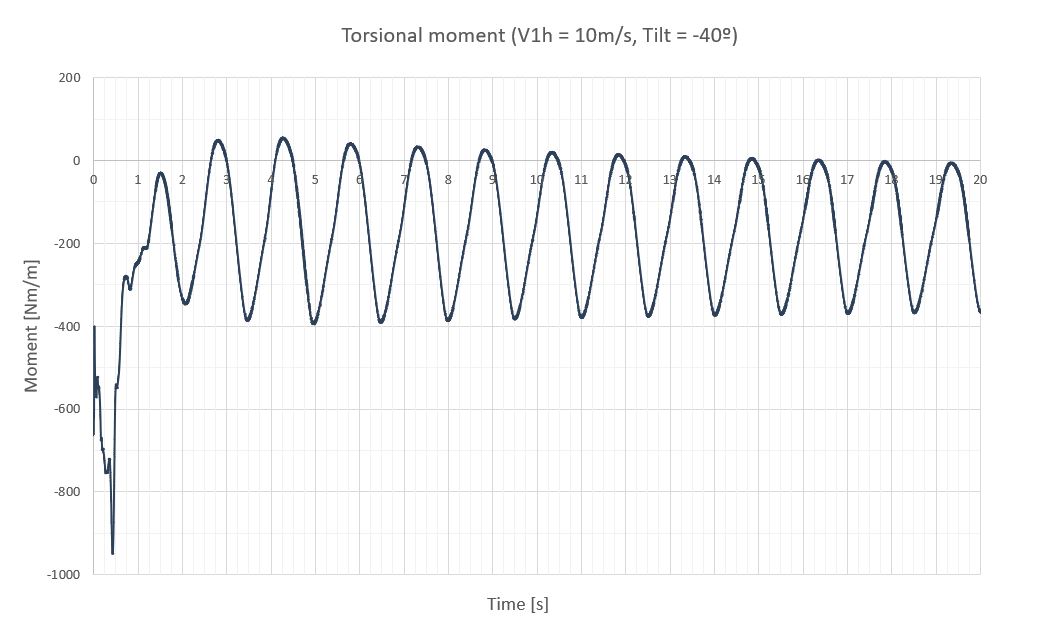
| -40 | 1.48 | 0.68 | -197 | ±169 | -366 | -0.55 | ±0.57 | -1.12 |
| -20 | 0.80 | 1.25 | -236 | ±7 | -243 | -0.66 | ±0.04 | -0.70 |
| 0 | 0 | 0 | -200 | 0 | -200 | -0.56 | 0 | -0.56 |
| 20 | 0.80 | 1.25 | 139 | ±8 | 147 | 0.39 | ±0.05 | 0.43 |
| 40 | 1.42 | 0.70 | 225 | ±46 | 271 | 0.63 | ±0.16 | 0.79 |
| 60 | 0 | 0 | 215 | 0 | 215 | 0.60 | 0 | 0.60 |
Se presentan los siguientes resultados:
- Los resultados calculados con el software CFD para un diseño aeroelástico de seguidores solares coinciden con los analíticos descritos en el post de desprendimiento de vórtices, donde el momento incidente y el giro de la sección se relacionan a través de la ecuación dinámica bidimensional del seguidor.
- Los transitorios son más largos para las inclinaciones positivas que para las negativas. Aunque pueden no mostrar la realidad exactamente, ya que en la simulación la velocidad del viento sube de 0 a 10m/s instantáneamente, pero en realidad el viento lo hace paulatinamente.
- Las vibraciones del seguidor a una velocidad de abatimiento en el régimen permanente pueden considerarse cuasi-estacionarias, ya que el viento no tiene energía suficiente para mantener una oscilación importante. Los mayores giros de la última sección se detectan a 40º de inclinación y no sobrepasan los 1.12º. Este comportamiento de estabilidad se debe en gran medida a los coeficientes de rigidez (k) y amortiguamiento (ξ) definidos para evitar el galope torsional y la divergencia torsional.
- Se observa que para la inclinación de 20º los momentos y giros máximos del seguidor son menores que en la posición horizontal, lo que podría hacernos pensar que es una posición más estable. De hecho, lo es para velocidades bajas de viento, por lo que nos llevaría a elegirla como posición de abatimiento. Nada más lejos de la realidad. Si bien la inclinación de 20º es más estable que la posición horizontal para velocidades de viento en operación ( V_{1h} \small < 10m/s ), no lo es frente a las velocidades de supervivencia de la planta ( V_{1h} \small = 30m/s ) como se verá en los siguientes apartados.
La posición de abatimiento o defensa elegida para los seguidores debe soportar los momentos inducidos por el desprendimiento de vórtices de la velocidad de viento de supervivencia de la planta ( V_{surv,1h} \small = 30m/s ). Dado que a esta velocidad el viento tiene mucha energía, los giros de la sección extrema del seguidor serán amplios, por lo que entrará en una oscilación de amplitud considerable, produciendo momentos importantes en la unión del tubo de torsión con el mecanismo. Ya que el tubo de torsión es el elemento estructural que soporta estos momentos oscilantes, deberá asegurarse que no se rebasa su límite elástico.
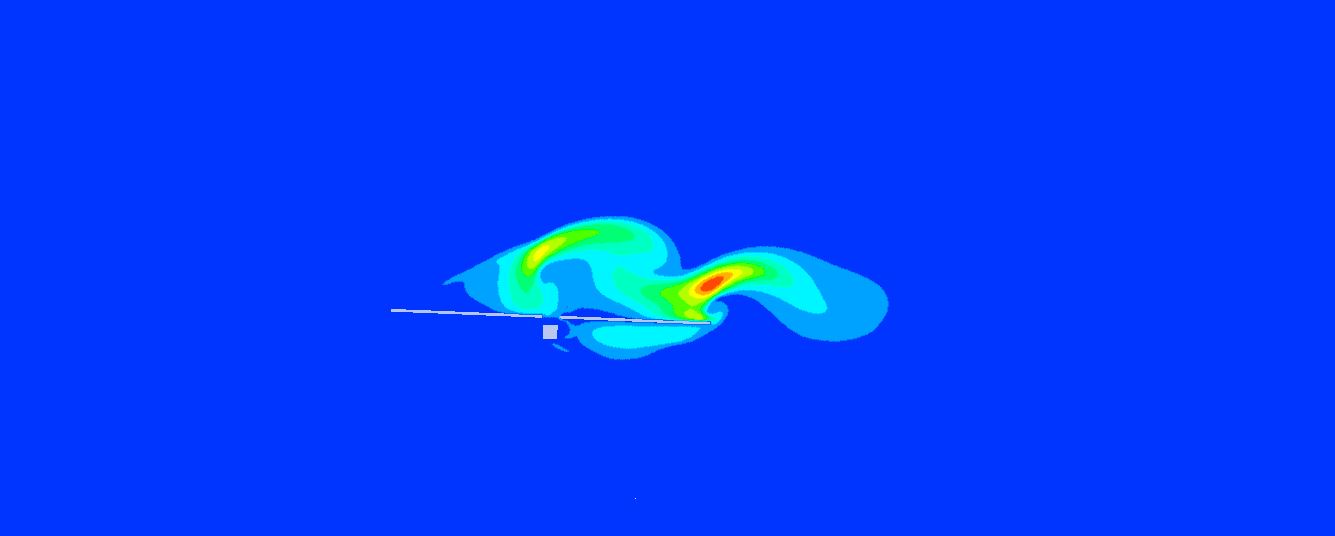
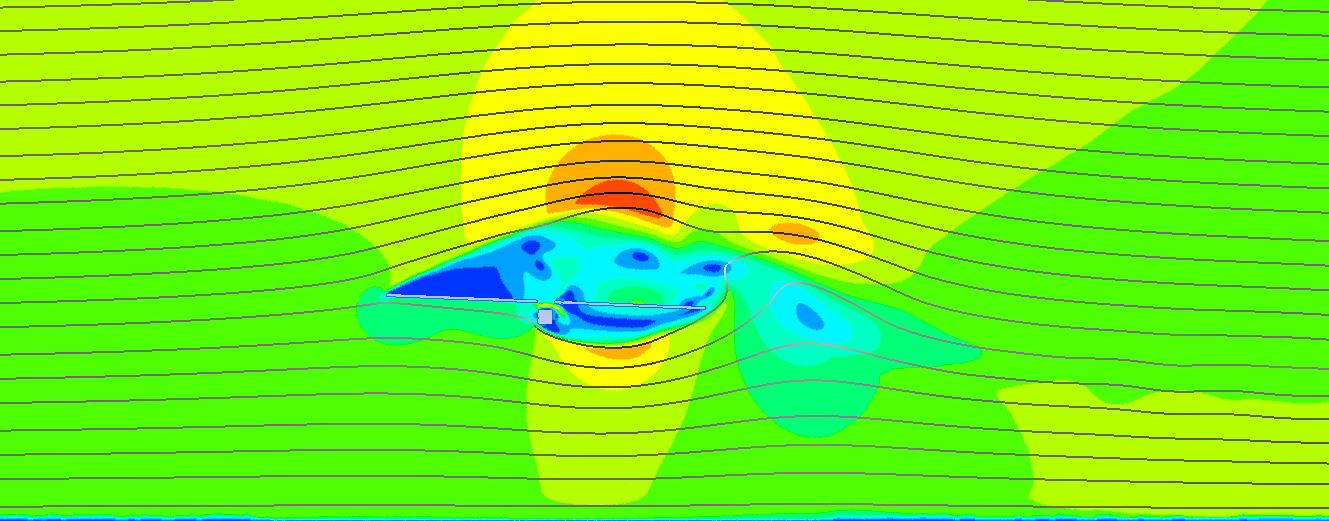
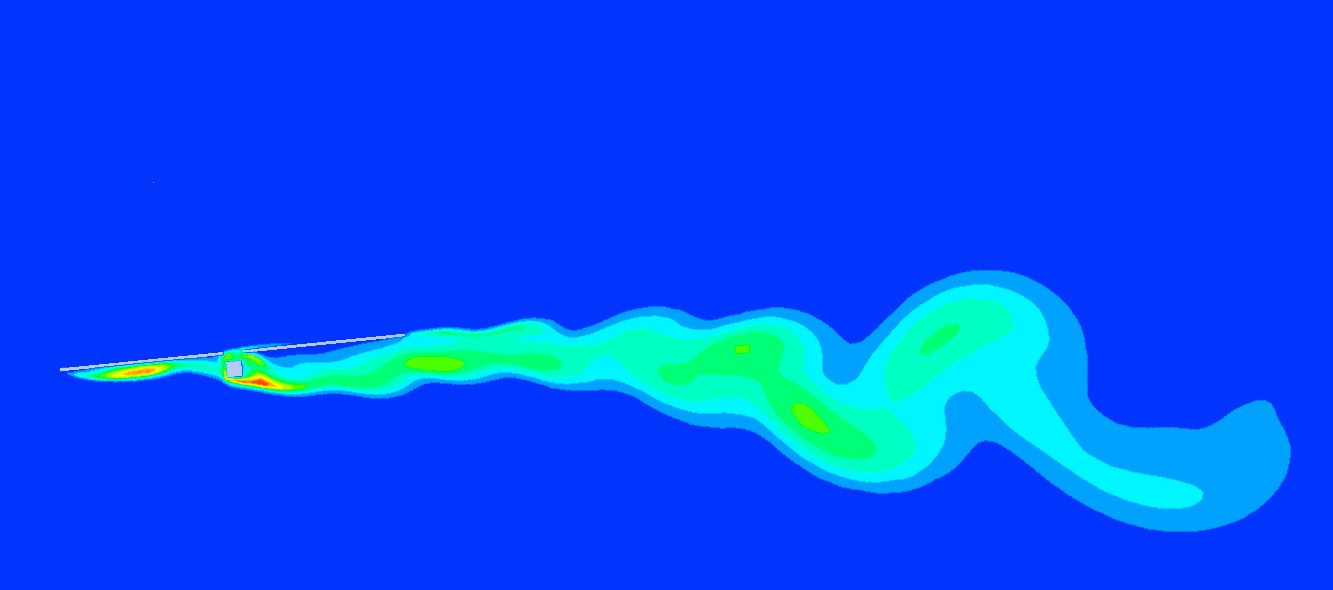
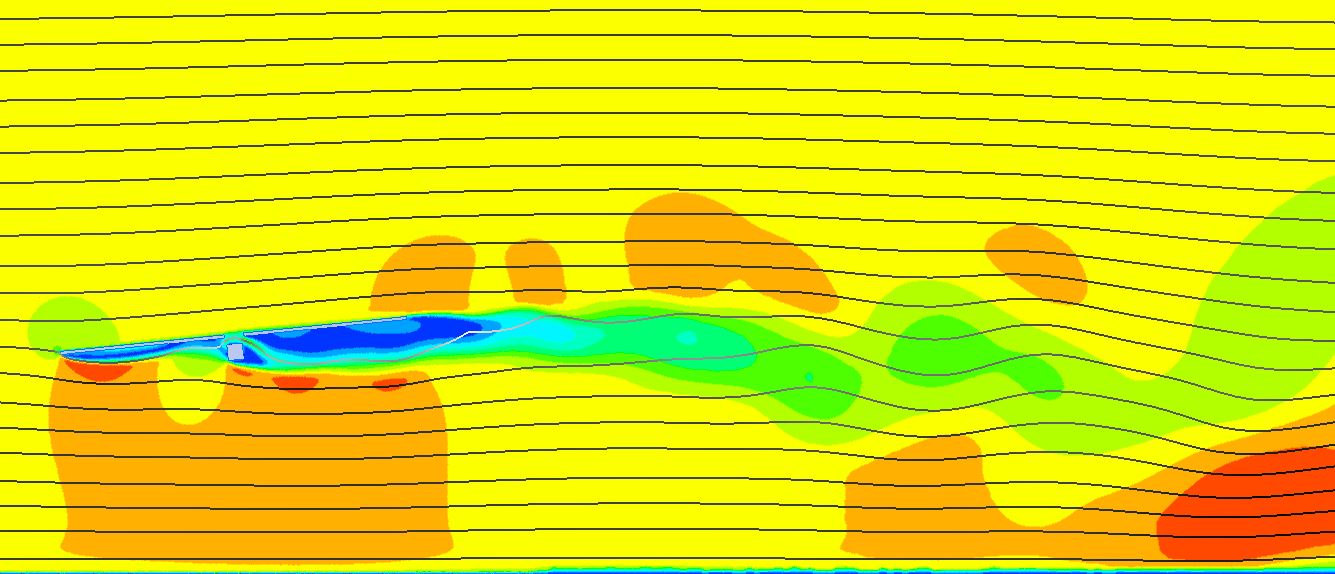

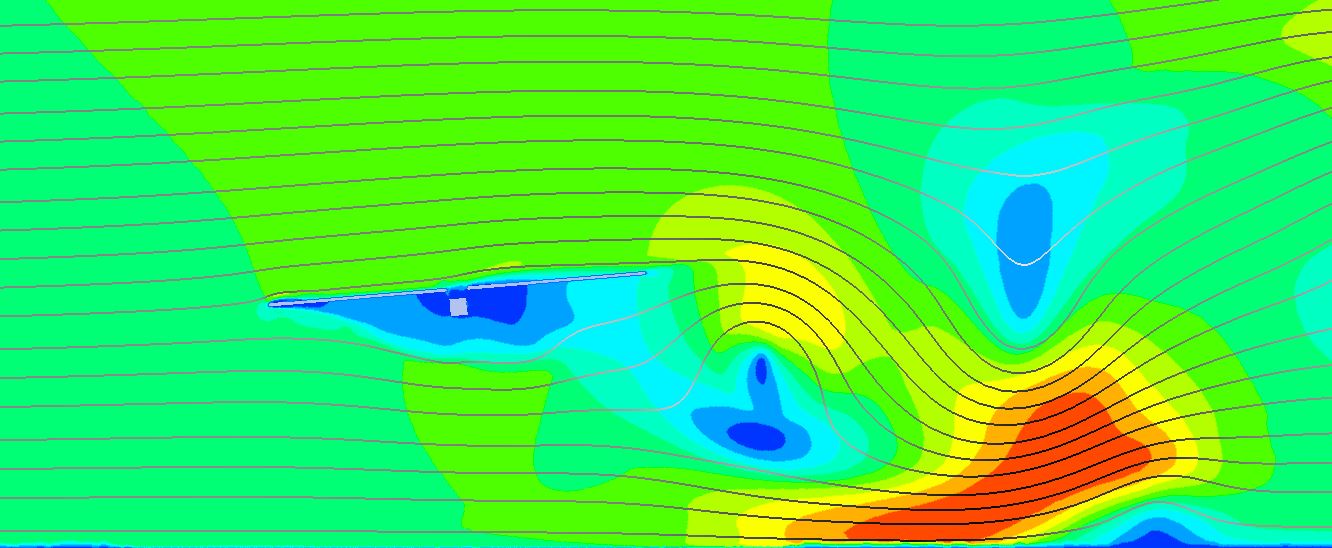
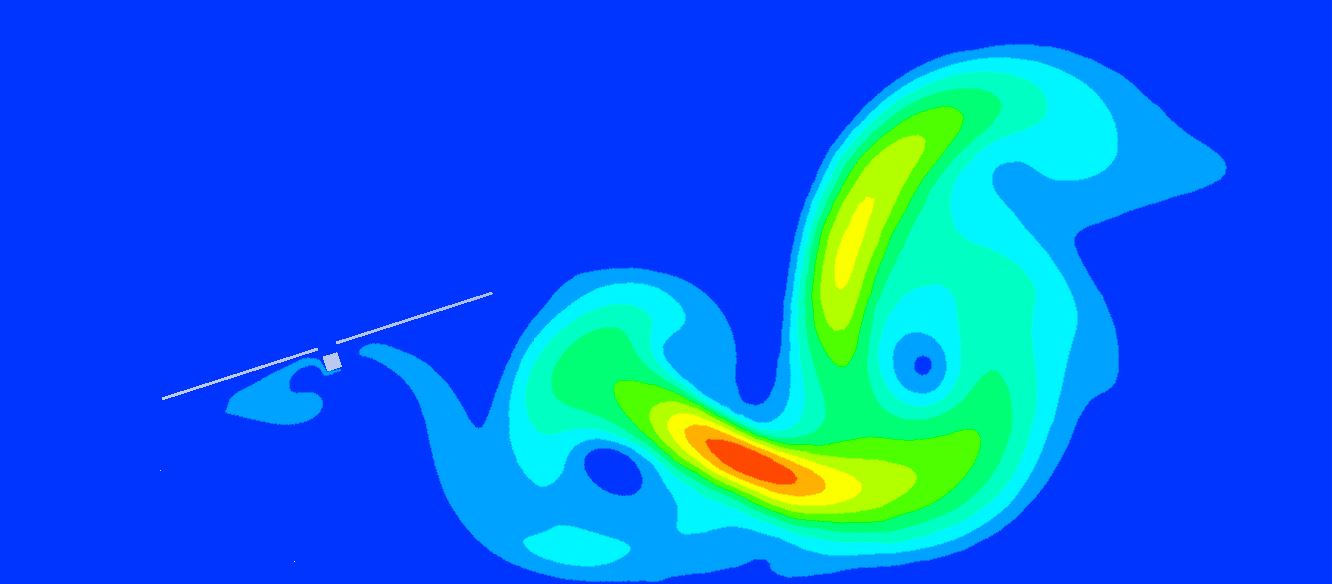
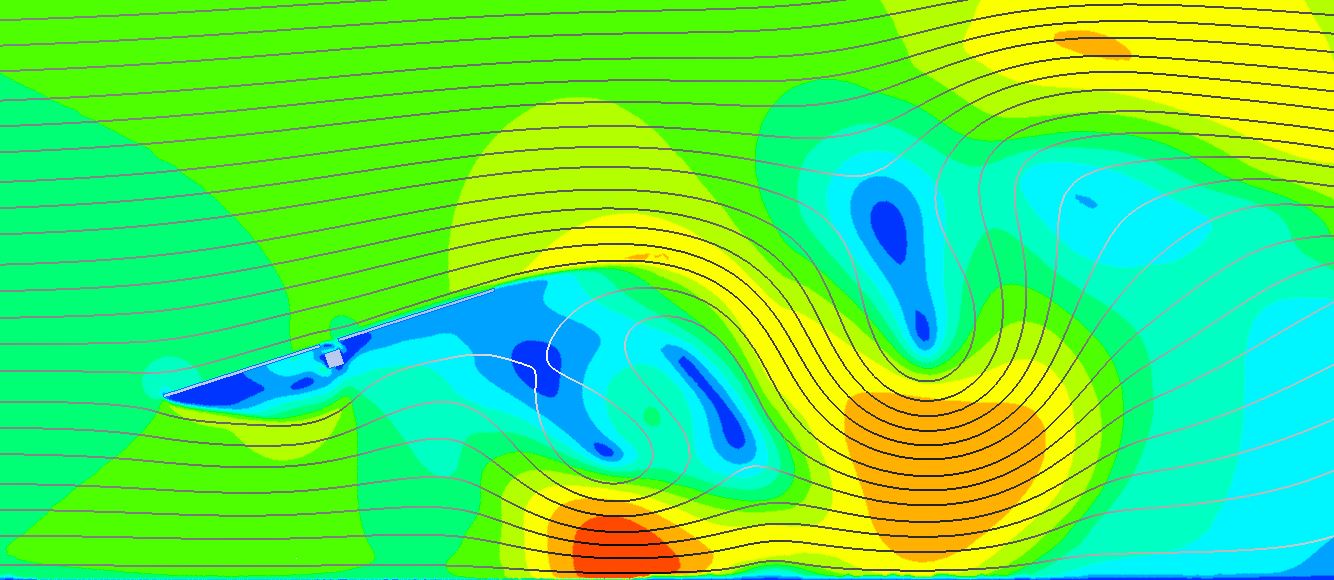
El estudio de las diferentes inclinaciones del seguidor para la velocidad de abatimiento ( V_{stow, 1h} = 10m/s ) en el diseño aeroelástico de seguidores nos marcaba la inclinación de 20º como la que menos oscilaciones producía sobre el seguidor debido a desprendimiento de vórtices, por lo que podría ser la nueva posición de abatimiento.
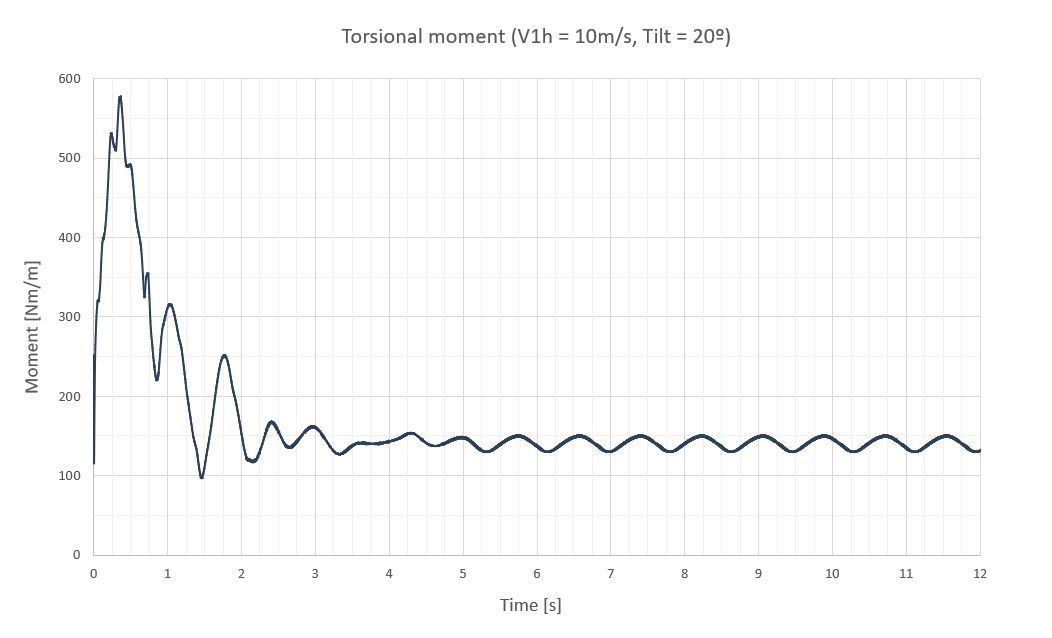
Era necesario, pues, confirmar que dicha posición (20º) producía menores momentos oscilantes que la posición de defensa tradicional de 0º a la velocidad de supervivencia de la planta ( V_{surv, 1h} = 30m/s ). Nuestros estudios aeroelásticos confirman que no es así debido a que la energía del viento es mucho mayor y la superficie expuesta de la posición de 20º es determinante para que se produzcan momentos muy altos que suponen el colapso tanto del tubo de torsión como del mecanismo central.
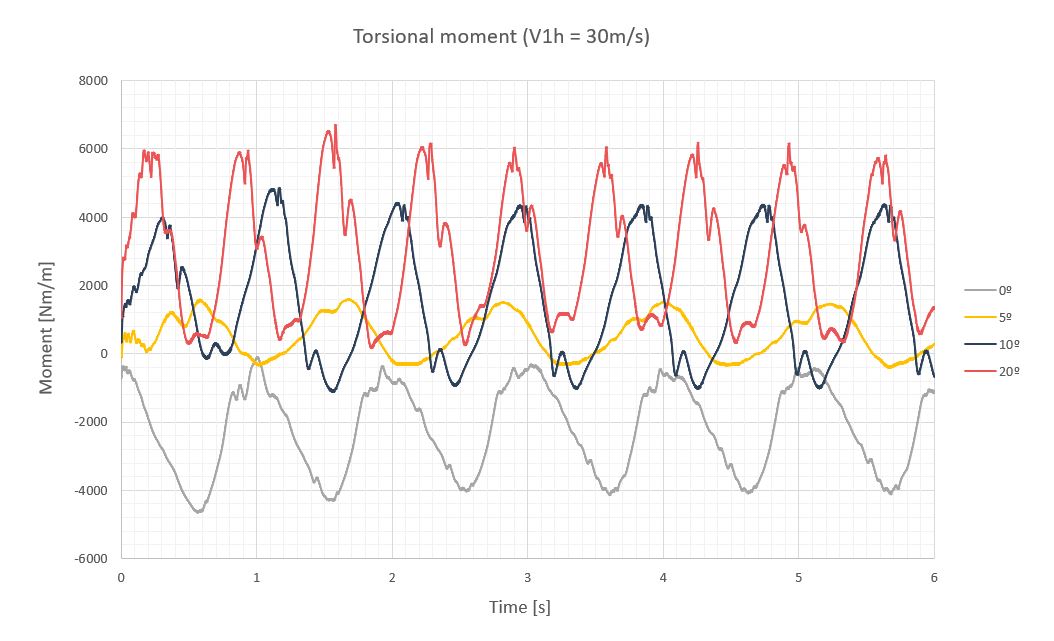
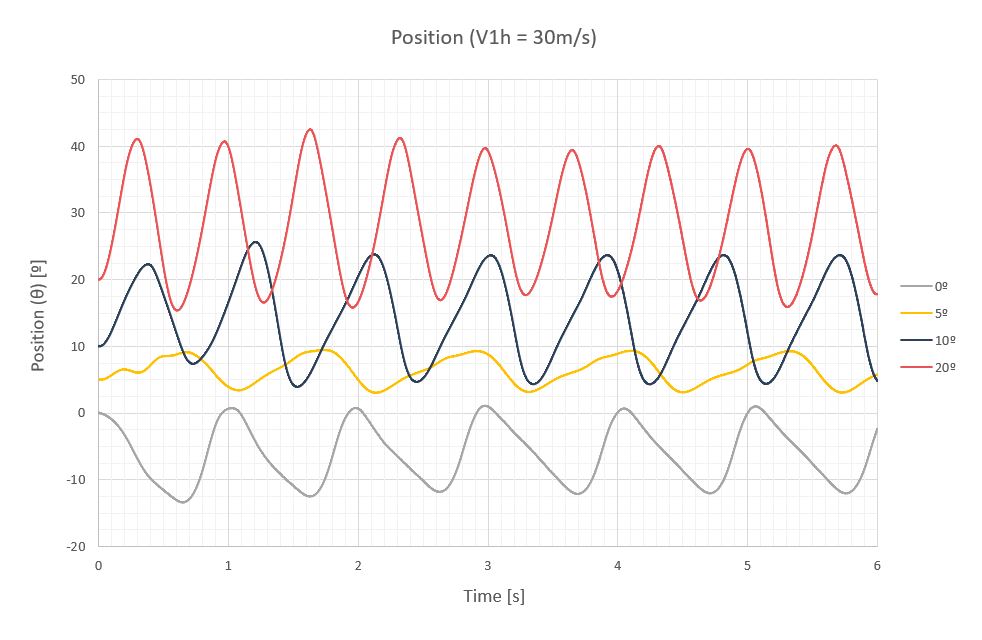
Dado que los momentos producidos a 0º eran totalmente negativos y los producidos a 20º totalmente positivos, hacía pensar que una posición intermedia entre ambas podía proporcionar momentos oscilantes más bajos. Estudios sobre las posiciones de 10 y 5º confirmaban esta conjetura, donde la inclinación de 5º aparecía como la nueva posición de defensa con momentos oscilantes máximos un 75% más bajos con respecto a la inclinación de 20º y un 65% más bajos con respecto a 0º. También, la reducción de los giros de la última sección es considerable pasando de -10 y 20º para las inclinaciones de 0º y 20º a solo 4º. La tabla siguientes muestra estos valores.
| Tilt [º] | T [s] | f [Hz] | Mest [Nm/m] | Ma [Nm/m] | Mmax [Nm/m] | Δθest [º] | Δθa [º] | Δθmax [º] |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | -2200 | ±1900 | -4100 | -6.13 | ±6.54 | -12.68 |
| 5 | 1.16 | 0.86 | 568 | ±883 | 1450 | 1.58 | ±2.87 | 4.45 |
| 10 | 0.9 | 1.11 | 1630 | ±2630 | 4260 | 4.54 | ±9.55 | 14.10 |
| 20 | 0,69 | 1.45 | 3000 | ±3000 | 6000 | 8.36 | ±13.00 | 21.69 |
Si comparamos estas gráficas con los casos de abatimiento:
- El régimen permanente se alcanza más rápido a velocidades altas de viento.
- El viento posee la energía suficiente para hacer girar el seguidor de forma importante, por lo que los momentos producidos deberán ser comprobados para el cálculo del tubo de torsión y los límites del mecanismo.
Bataneo (Buffeting)
Existe un cuarto fenómeno llamado bataneo y bataneo de estela que debe ser considerado en el diseño aeroelástico de seguidores, ya que introduce aumentos instantáneos de la carga calculada en el desprendimiento de vórtices.
El bataneo se debe a los cambios de presión del viento sobre la estructura debido a la turbulencia. Esto hace que la velocidad de viento oscile alrededor una velocidad media ( V_{1h} ), alcanzando picos positivos ( V_{3s} ) y negativos alrededor de dicha velocidad media, dando lugar a las velocidades a considerar en los códigos de edificación.
Este fenómeno aeroelástico introduce aumentos de presión instantáneos sobre la estructura. Como hemos mencionado anteriormente la relación máxima entre estas velocidades es de 1.52 pero en cada punto de la estructura existirá un valor entre -1.52 y 1.52 de forma aleatoria. Lo que sí se puede confirmar es que, si existe una configuración de puntos de presión definida sobre la superficie del seguidor en un instante determinado, esta misma configuración puede repetirse aleatoriamente en el tiempo.
Los códigos técnicos consideran esta velocidad pico para todas las secciones de la estructura, pero realmente, y debido a la longitud del seguidor, solo se producen en determinadas zonas y nunca a la vez sobre toda la superficie. Es por lo que los estándares de edificación siempre se encuentran por el lado de la seguridad y es por lo que los ensayos de túneles de viento ajustan mejor la carga real sobre la estructura considerando solo las configuraciones máximas de estas presiones pico que ocurren en la realidad.
En nuestro post Buffeting en seguidores solares se define un valor de ráfaga medio ( \bar G ) que se utilizará en mayorar los momentos de torsión por este fenómeno.
\bar G = \Large \frac{1 + 1.52}{2} \normalsize = 1.26
Este parámetro que mayora las cargas de viento debido a la turbulencia no debe ser aplicado a las filas de seguidores que se encuentran totalmente inmersas en la estela de seguidores contiguos, como ocurre en las posiciones más verticales del seguidor [-60º, 40º] y [40º, 60º], ya que nunca llegarán a ver dicha turbulencia solamente la estela del seguidor adyacente.
Por el contrario, el bataneo de estela afecta únicamente a seguidores interiores y es una inestabilidad debida a los cambios de presión en el viento que provoca el desprendimiento de vórtices de una estructura que se encuentra entre el flujo de viento y la estructura de cálculo. Se trata por tanto de un segundo problema de resonancia, ya que si el desprendimiento de vórtices provoca una oscilación sobre la estructura que abandona, también provocará una oscilación sobre la siguiente estructura que golpea, ya que ambas estructuras son iguales y con la misma frecuencia natural.
Como resultado, aparecerá una vibración de amplitud y frecuencia, a priori, diferentes de las del seguidor que afronta el flujo de viento totalmente limpio, por lo que cada fila de seguidores debe ser comprobada para ver si existen modificaciones significativas con respecto a la fila perimetral que cambien el diseño del seguidor.

A efectos prácticos, se puede considerar que el aumento de los momentos de torsión debidos al bataneo de estela de las filas interiores con respecto a las filas perimetrales es de un 15%.
Componentes mecánicos
Para calcular las tensiones máximas tangenciales debidas a la torsión sobre el tubo, necesitamos los momentos producidos a la velocidad de viento de supervivencia de la planta ( V_{surv,3s} = 45m/s ) en la posición de defensa.
Por medio de software CDF, el momento estático (Mest) y el oscilante (Ma) han sido calculado en párrafos anteriores para la velocidad media V_{surv,1h} = 30m/s y la posición de defensa de 5º. Los valores que buscamos para calcular el tubo de torsión deben considerarse con la velocidad pico a la frecuencia de desprendimiento del torbellino (f), teniendo en cuento el aumento de carga por bataneo ( \bar G ), en su caso.:
A continuación, se exponen algunos valores indicativos para la primera fila perimetral de seguidores de la planta.
M_{est,V3s} = \bar G M_{est,V1h} = 900Nm/m
M_{a,V3s} = \bar G M_{a,V1h} = 1400Nm/m
M_{max} = M_{est} + M_a = 2300Nm/m
f = 0.86Hz
Para obtener las tensiones en el tubo, estos momentos deben analizarse en un modelo dinámico forzado tridimensional del seguidor, ya que el modo de vibración también es tridimensional.
Los máximos momentos aparecerá en la unión del tubo de torsión con la brida que abrocha el mecanismo. Se expone a continuación la gráfica de tensiones en esta zona debido a los momentos y frecuencia de cálculo:
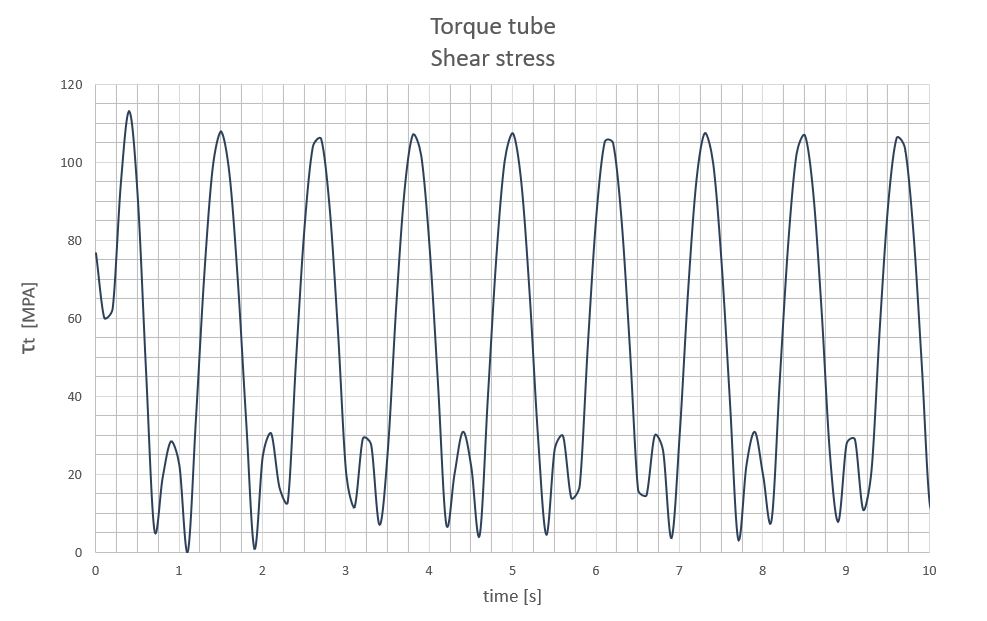
Con este nivel de tensiones, podemos afirmar que no se produce el colapso del tubo debido a las tensiones tangenciales de torsión. A estas tensiones habría que sumar las producidas por las fuerzas de viento de resistencia y sustentación, pero debido a que el nivel de tensiones tangenciales por torsión se encuentra por debajo de la mitad del limite elástico del material, se tiene un margen considerable para soportar estas cargas.
Los criterios de diseño o comprobación del mecanismo que dependen de los momentos de torsión son los descritos en este post y que resumimos aquí. Se debe tener en cuenta que el mecanismo central soporta siempre el doble de cargas que un solo tubo de torsión.
Los momentos máximos para el mecanismo aparecerán para la posición de abatimiento (5º) y velocidad de supervivencia de la planta.
A continuación, se exponen los valores que no debe sobrepasar el mecanismo para el seguidor definido en los siguientes casos:
- Para la posición de abatimiento (5º) y velocidad pico de supervivencia de la planta V_{surv,3s} = 45m/s :
Limite estático > 2L · Mmax_{ Vsurv,3s} = 79600Nm
Con:
\small Mmax_{ Vsurv,3s} = \bar G Mmax_{ Vsurv,1h}
- Para cualquier posición del seguidor y velocidad de abatimiento pico de la planta V_{stow,3s} = 15m/s :
Límite dinámico máximo > 2L · Mmax _{ Vstow,3s} = 20100Nm
Con:
\small Mmax_{ Vstow,3s} = \bar G Mmax_{ Vstow,1h}
- Para cualquier posición del seguidor y velocidad de abatimiento media de la planta V_{stow,1h} = 10m/s :
Límite dinámico nominal > 2L · Mmax_{ Vstow,1h} = 12660Nm
Siendo L la longitud de cada uno de los tubos de torsión y \bar G el factor que aumenta de carga debido a la turbulencia en el bataneo.
Si no se cumplen estas tres condiciones de deberá instalar un mecanismo con límites de torsión más altos o incrementar la rigidez (k) y el amortiguamiento del sistema (ξ) para disminuir los momentos incidentes sobre el seguidor producidos por el desprendimiento de vórtices.
La fatiga es un fenómeno mecánico por el que se llega al colapso del material debido a cargas repetitivas de valor inferior a las que provocarían la plastificación del material en casos estáticos.
En seguidores solares de un eje, la fatiga puede aparecer en la unión del tubo de torsión con el con el mecanismo, concretamente en la soldadura de la brida de unión al tubo de torsión, debido a entallas y pequeñas imperfecciones de dicha soldadura, lo que provoca áreas de aparición de microgrietas que van creciendo a lo largo del tiempo debido a la carga oscilante.
De los resultados expuestos, si el seguidor está diseñado con la rigidez (k) y amortiguamiento (ξ) para cumplir con los criterios de divergencia y galope, los momentos que produce el desprendimiento de vórtices del viento para velocidades igual o menores que las de abatimiento no parece tener amplitudes demasiado altas en régimen permanente como para rebasar el límite de fatiga del material.