Proceso del diseño aeroelástico
Mostramos el proceso del diseño aeroelástico esquematizado que relaciona las variables más importantes que intervienen en los fenómenos aeroelásticos así como los componentes de un seguidor de un eje que se encuentran afectados o soportan las cargas de estas inestabilidades.
Antes de comenzar con el proceso de cálculo aeroelástico es necesario tener definida la geometría del seguidor que nos proporcionará su frecuencia natural (n) y su modo de vibración asociado:
| Material | Yield Limit [MPa] |
|---|---|
| S275JR | 250 |
| S355JR | 320 |
-
- Límite estático (holding torque) o valor máximo de cargas de torsión que puede soportar completamente parado.
-
- Límite dinámico nominal (nominal torque) o valor nominal que puede mantener cuando se mueve. Este valor debe asociarse a velocidades medias de viento ( V_{1h} ).
-
- Límite dinámico máximo (maximum torque) o valor máximo que puede mantener por un instante corto de tiempo, normalmente se considera durante 3 segundos, por lo que se coteja con la máxima velocidad pico de viento ( V_{3s} ) que se alcanza instantáneamente para una velocidad media de viento dada ( V_{1h} ).
Cualquier mecanismo soporta más carga estando parado que en movimiento. La relación entre el límite estático y el dinámico máximo suele estar entre 2 y 3.
Para esta geometría se obtiene una frecuencia natural de 2.1Hz que proporciona el modo torsional de vibración.
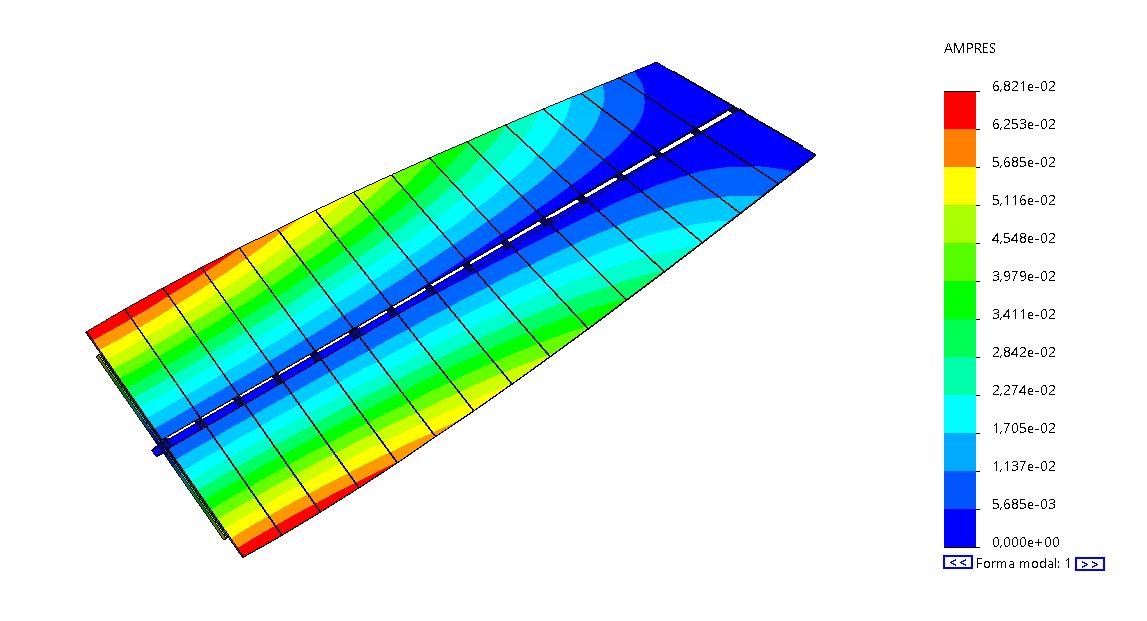
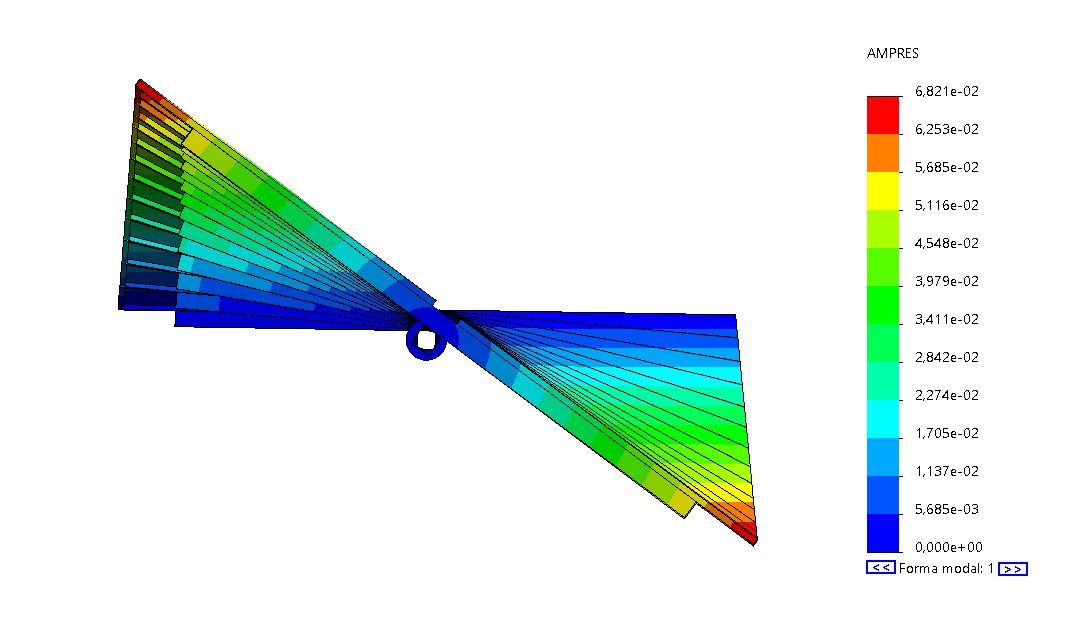
Para comprobar completamente las cargas de torsión sobre los componentes del seguidor, es necesario tener en cuenta los momentos de torsión debidos al descentramiento del peso que introducen los módulos fotovoltaicos cuando se inclinan por el movimiento de operación del seguidor. Por lo que la torsión vendrá dada por la acción de la carga de viento más el momento que proporciona el peso del propio seguidor.
Los fenómenos aeroelásticos introducen principalmente tensiones tangenciales ( \tau_t ) debidas a los momentos de torsión ( M ), pero las cargas de resistencia y sustentación debidas a las fuerzas de viento ( F ) producirán tensiones normales de flexión ( \sigma_b ) y tensiones tangenciales debidas esfuerzos cortantes ( \tau_c ) que, si bien son más pequeños que las tensiones tangencias debidas a la torsión ( \tau_t ), deben computarse de acuerdo a la fórmula de Von Mises ( \sigma_{VM} ) para obtener la tensión total sobre los componentes del seguidor.
\sigma_{VM} = \sqrt{\sigma_b^2 + 3 (\tau_t + \tau_c)^2}
Modelo bidimensional vs tridimensional
El proceso del diseño aeroelástico se basa en un modelo bidimensional en el solo te tiene en cuenta la deformación o giro de la ultima sección del seguidor. Ya que el modo de vibración es una torsión lineal del seguidor, se puede saber el giro de las demás secciones por la su distancia a la sección última dado que también se conoce la longitud total del tubo de torsión. No hay que confundir los parámetros bidimensiones de inercia (I) y rigidez (k) con los tridimensionales, a los que llamaremos \hat I y \hat k para distinguirlos.
Dado la deformación de la última sección del seguidor del modelo tridimensional cuando se la aplica un momento linealmente distribuido, se puede ajustar los valores de inercia ( I ) y rigidez ( k ) para conseguir la misma rotación para la misma carga, esta vez por metro, en el modelo bidimensional.
La rigidez de un sistema tridimensional ( \hat k ) puede definirse como:
\hat k = (2\pi n)^2 \hat I
Siendo n la frecuencia natural del modo de vibración torsional y \hat I la inercia tridimensional en el eje de torsión que normalmente se obtiene de los programas de diseño (CAD). Los programas de diseño proporcionan la inercia de giro de toda la estructura con respecto del eje del modo de vibración ( \hat I_{cad} ), pero no calculan la inercia que contribuye a este modo. También se sabe que la inercia que contribuye a un modo torsional de vibración con uno de los extremos fijos es una tercera parte de la inercia de la estructura si ésta gira con los dos extremos libres por lo que:
\hat I = \Large \frac{1}{3} \normalsize \hat I_{cad}
Escribiendo de nuevo la rigidez, pero esta vez con dependencia de la inercia que nos proporciona un software de diseño tenemos que:
\hat k = \Large \frac{1}{3} \normalsize (2\pi n)^2 \hat I_{cad}
Por otro lado, podemos hacer una aproximación de la rigidez (k) e inercia (I) bidimensionales a través del giro de la última sección del seguidor tridimensional con una carga linealmente distribuida (m).
\theta_{ 3d} = \theta_{ 2d}
\Large \frac{1}{2} \frac{m L^2}{GJ} \normalsize = \Large \frac{m}{k}
Donde la rigidez (k) es igual a:
k = \Large \frac{2GJ}{L^2}
Siendo:
- G: el módulo de cizalladura del material
- J: Inercia a torsión de la sección
- L: la longitud del tubo a torsión
Esta formulas son aproximadas, ya que se está teniendo en cuenta que la rotación del seguidor solo depende la rigidez del tubo de torsión, y mayoritariamente es así. Se pueden hacer modelos tridimensionales más exactos donde además se considera la rigidez de los módulos fotovoltaicos y los perfiles que lo soportan.
Determinación de la rigidez (k)
El proceso del diseño aeroelástico comienza con el cálculo de la rigidez (k) mínima que debe tener el seguidor para garantizar que la divergencia torsional no se produce para velocidad más bajas que la velocidad de supervivencia de la planta ( V_{surv,1h,10m} ≈ 30m/s ).
k = \Large \frac {1}{2} \normalsize \rho U_{cr}^2 b^2 \Large \frac{ \partial c_m}{\partial \alpha} \normalsize
La rigidez (k) en un seguidor de un eje es proporcionada principalmente por la rigidez de su tubo de torsión y depende de la forma de su sección. Si la rigidez (k) que proporciona el seguidor no es suficiente para cumplir con los criterios de divergencia torsional, se tienen que modificar las dimensiones del tubo de torsión para aumentar su rigidez.
Como hemos visto en líneas anteriores:
k = \Large \frac{2GJ}{L^2}
Ya que el modulo de torsión del acero no se puede cambiar porque es una característica prácticamente constante para todos los aceros, la rigidez (k) solo se puede aumentar si disminuimos la longitud del tubo de torsión o aumentamos su inercia a torsión (J)
La inercia a torsión para perfiles de sección cuadrada de pared delgada ( J_{\#} ) puede aproximarse por la fórmula de Bredt como:
J_{\#} = e (a-e)^3 \approx ea^3
Siendo:
- e: el espesor del tubo de torsión
- a: el lado de la sección cuadrada
Dado que la inercia a torsión (J) depende del lado de la sección al cubo, es más fácil hacer pequeñas modificaciones a este parámetro para obtener resultados más significativos. Por otro lado, aumentar el espesor de un tubo siempre es más caro que aumentar su lado para obtener mejoras seccionales.
Determinación del amortiguamiento (ξ)
Una vez que la rigidez del sistema (k) cumple con los criterios de divergencia torsional, este parámetro debe ser tenido en cuenta en el cálculo del coeficiente de amortiguamiento (ξ) que asegure que el seguidor no entre en galope torsional por debajo de la velocidad de supervivencia de la planta ( V_{surv,1h,10m} ≈ 30m/s ).
\xi = \Large \frac {1}{16} \frac {\rho U_{cr}^2 b^3 \frac{\partial c_m}{\partial \alpha}}{I \omega_n} \normalsize
Esta inestabilidad aeroelástica depende fuertemente del ancho de la sección del seguidor (b), como se puede comprobar este parámetro está elevado al cubo. Por esta razón seguidores de igual longitud con una sola fila de módulos son muchísimo más estables frente al galope torsional.
Este factor (ξ) es el que define el sistema de amortiguamiento a instalar en el seguidor, ya que por si mismo la estructura no tiene amortiguamiento suficiente para evitar el galope. Recordemos que este valor está por en torno a 0.01 para seguidores sin un amortiguamiento físico instalado.
Por lo tanto, el valor del coeficiente de amortiguamiento (ξ) será empleado para el diseño de amortiguadores que se instalarán en cada pilar del seguidor para evitar el galope torsional.
Desprendimiento de vórtices
Con la rigidez (k) y el amortiguamiento (ξ) definidos para cumplir divergencia y galope, el siguiente paso del proceso del diseño aeroelástico es analizar el desprendimiento de vórtices que produce un momento oscilante sobre el seguidor. Estos momentos dependen de la frecuencia de la separación del torbellino (f), que suele estar en torno a 1Hz, por lo que cuanto más alta sea la frecuencia natural del seguidor, menor será la posibilidad de que entre en resonancia, admitiendo mayores cargas. Un análisis del comportamiento de este seguidor para velocidades de viento de abatimiento y supervivencia se muestran en nuestro post diseño aeroelástico de seguidores.
Una mayor frecuencia natural del sistema (n) implica una mayor rigidez de acuerdo con la formula:
n = \Large \frac {1}{2\pi} \sqrt{\frac{k}{I}}
Esta inestabilidad afecta a componentes importantes del seguidor en los 4 siguientes escenarios:
Hay que señalar que el mecanismo mueve dos tubos de torsión, por lo que siempre soportará una carga del orden del doble con respecto a los tubos de torsión.
Si alguno de estos supuestos no se cumpliese, habría que aumentar de nuevo la rigidez (k) y/o el amortiguamiento (ξ).
Los resultados de los cálculos analíticos, así como lo que provienen de simulaciones CFD deberían ser corroborados por ensayos de túneles de viento aeroelásticos para confirmar que no se produce la aparición de los fenómenos de instabilidad a baja escala, lo que cerraría definitivamente el diseño aeroelástico del seguidor.