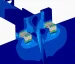
Esfuerzos de tracción en tornillería pretensada

Un tornillo pretensado que une dos o más piezas se encuentra sometido a una fuerza de pretensado ( $P$ ) que se emplea en estirar el tornillo ( $P_b$ ) y comprimir los elementos de unión ( $P_c$ ).

$P = P_b + P_c$

Pretensado y deformaciones en tornillería

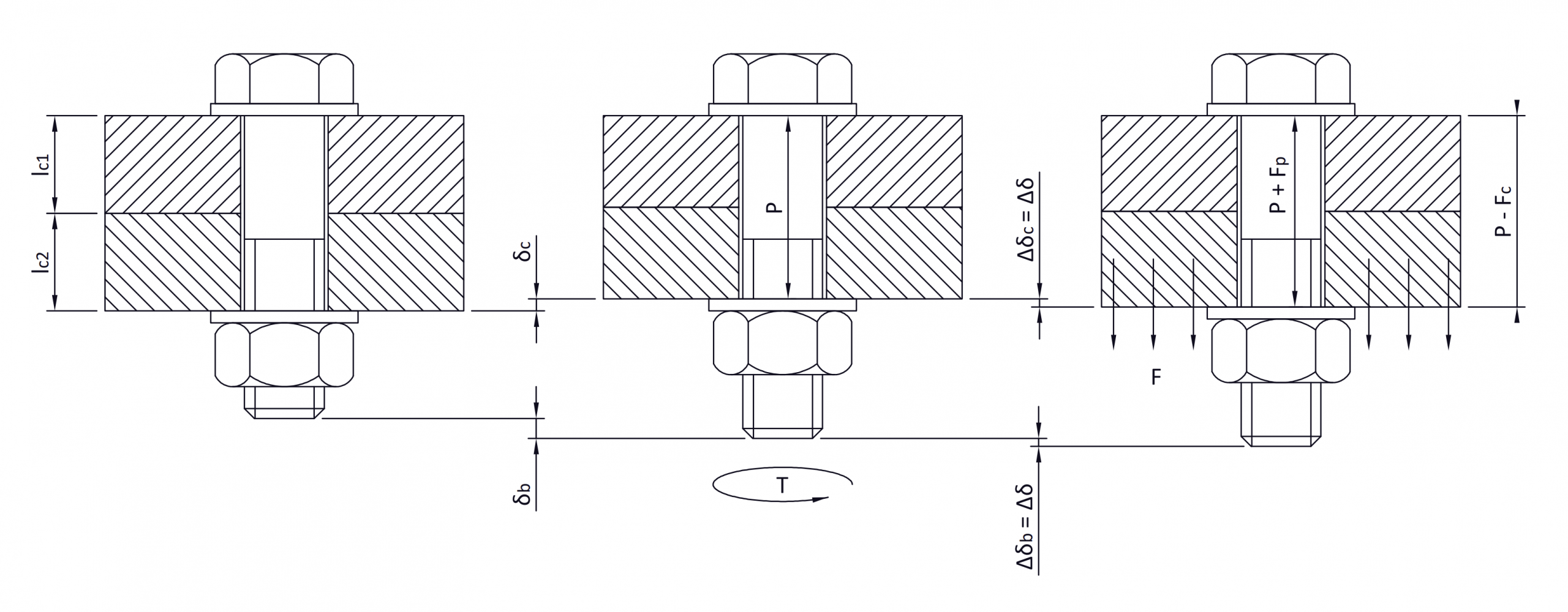
Al aplicar una fuerza de pretensado, el tornillo se deforma una longitud positiva ( $\delta_b$ ), se alarga, y a su vez, las piezas de unión se deforman una longitud negativa ( $\delta_c$ ), se acortan.

$\delta_b = \Large \frac{P_b}{K_b}$

$\delta_c = \Large \frac{P_c}{K_c}$

Donde:

$K_b$ : constante de rigidez del tornillo
$K_c$ : constante de rigidez de las piezas de unión

Gráfica en el pretensado

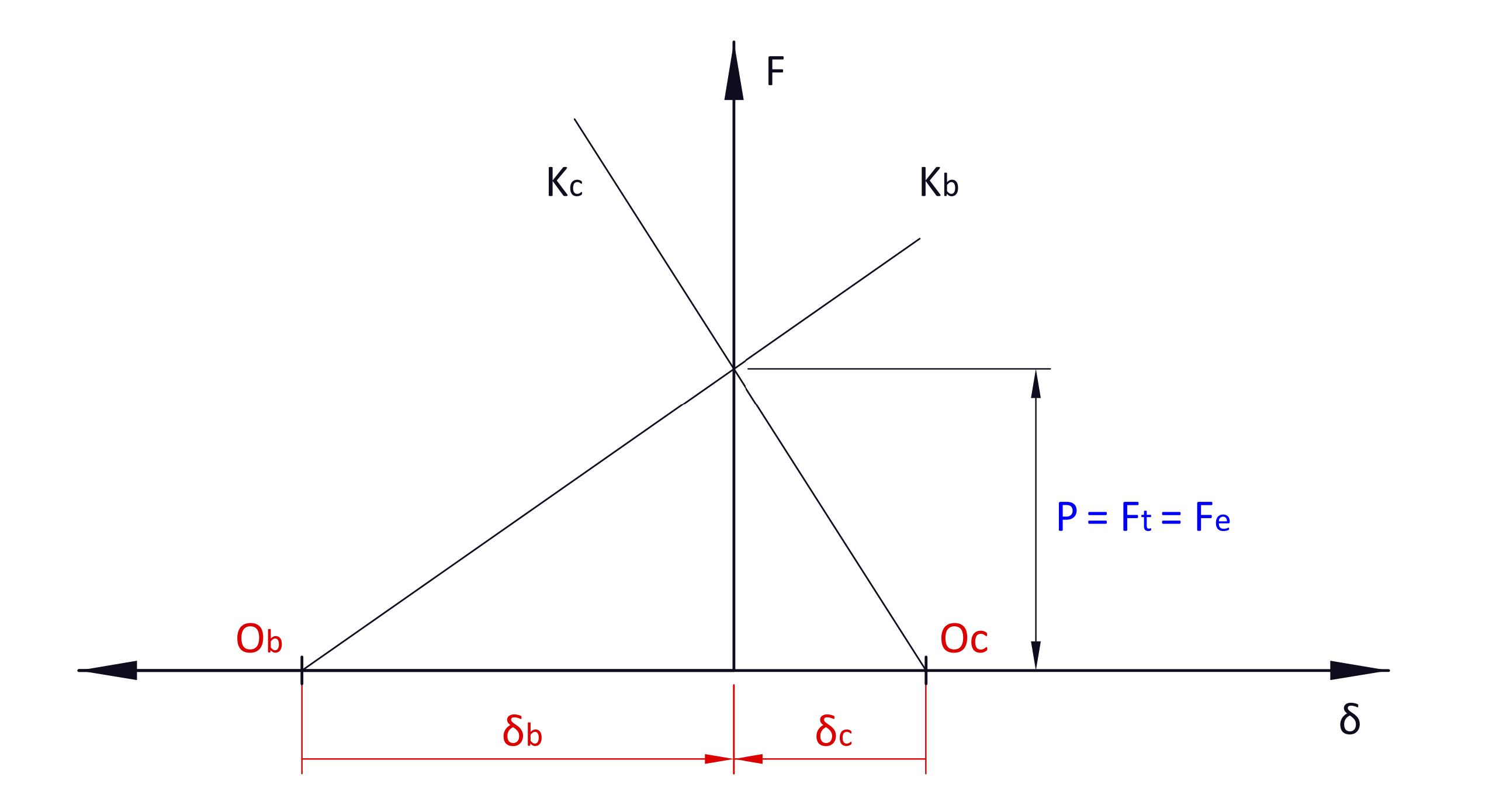
Al aplicar una carga exterior ( $F$ ) a través de las piezas de unión, el tornillo vuelve a alargarse de nuevo un desplazamiento ( $\Delta \delta_b$ ) debido a una fuerza $F_b$ y las piezas tienden a descomprimirse en un desplazamiento negativo ( $-\Delta \delta_c$ ) provocado por una fuerza $F_c$ .

Dado que la unión se encuentra en equilibrio se tiene que:

$F = F_b + F_c$

$\left | \Delta \delta_b \right | = \left | \Delta \delta_c \right | = \Delta \delta$

Aplicando las ecuaciones que relacionan la carga con el desplazamiento en el régimen elástico, tenemos que:

$\Delta \delta_b = \Large \frac{F_b}{K_b}$

$\Delta \delta_c = \Large \frac{F_c}{K_c}$

Sustituyendo:

$\Delta \delta = \Large \frac{F_b}{K_b} \normalsize = \Large \Large \frac{F_c}{K_c}$

$F_b = K_b \Large \frac{F_c}{K_c}\normalsize = K_b \Large \frac{F-F_b}{K_c}$

$F_b = \Large \frac{K_b}{K_b+K_c}\normalsize F = C F$

Con $C$ como la constante de rigidez de la unión:

$C = \Large \frac{K_b}{K_b+K_c}$

Análogamente, para $F_c$ tenemos:

$F_c = \Large \frac{K_c}{K_b+K_c}\normalsize F = (1- C) F$

Para calcular la constante de rigidez de la unión ( $C$ ), primero debemos determinar la constante de rigidez del tornillo ( $K_b$ ) y la constante de rigidez de los elementos de unión ( $K_c$ ). En nuestro post Rigidez en uniones atornilladas pretensadas el lector puede encontrar estimaciones de dichos parámetros.

Gráfica al aplicar la carga externa en el pretensado

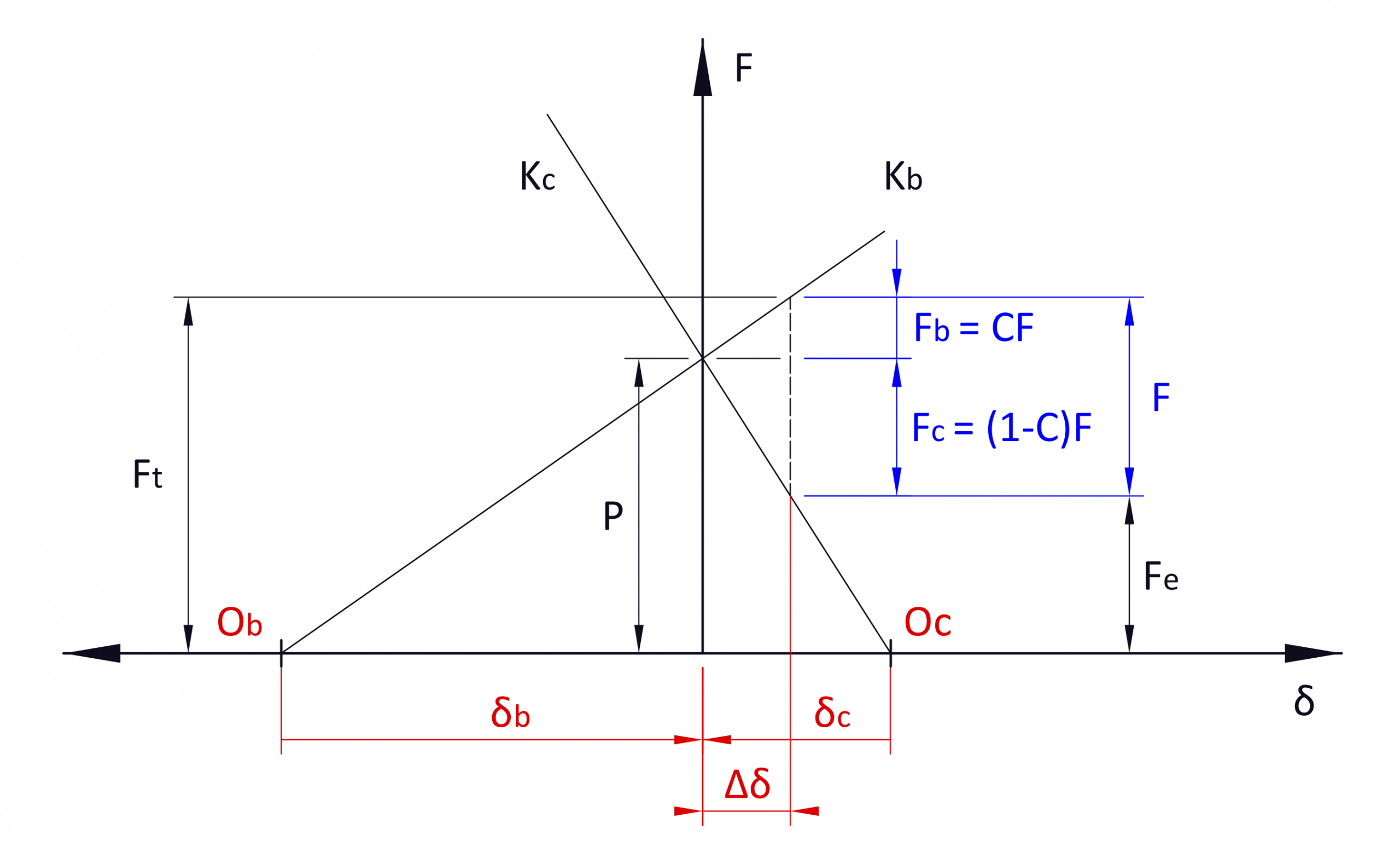
La carga final sobre el tornillo ( $F_t$ ) y sobre los elementos de unión ( $F_e$ ) después de aplicar la carga externa ( $F$ ) con un pretensado ( $P$ ) son:

$F_t = P+CF$

$F_e = P-(1-C)F$

Pretensado

Normalmente suele seleccionarse un pretensado ( $P$ ) comprendido entre:

$P_{min} \leq 0.6 A S_y \leq P \leq 0.8 A S_y \leq P_{max}$

Con valores altos para que los tornillos no tiendan a aflojarse por vibración:

$P = 0.75 A S_y$

Grade	Yield limit (Sy) [MPa]	Tensile limit (Su) [MPa]
5.8	400	500
8.8	640	800
10.9	900	1000
12.9	1080	1200

Pretensado mínimo
Pretensado máximo

Pretensado mínimo

Es el pretensado mínimo ( $P_{min}$ ) para que no ocurra la separación de los elementos de la unión debida a la fuerza exterior de tracción ( $F$ ). Esta condición la tenemos cuando:

$\Delta \delta_c = \delta_c$

$\Large \frac{F_c}{K_c}\normalsize = \Large \frac{P_c}{K_c}$

$P_{min} = F_c = \Large \frac{K_c}{K_b+K_c} \normalsize F = (1-C)F$

Pretensado máximo

Para cargas externas estáticas

Es el pretensado máximo que puede soportar el tornillo ( $P_{max-s}$ ) para que no se llegue a su límite de fluencia ( $S_y$ ) cuando éste se encuentra trabajando a una carga de tracción ( $F_b$ ), por lo que:

$F_y = P_{max-s} + F_b$

$P_{max-s} = S_y A - C F$

Donde:

$F_y$ : Fuerza que proporciona el límite de fluencia
$A$ : área resistente del tornillo

Para cargas oscilantes en fatiga

Es el pretensado máximo que puede soportar el tornillo ( $P_{max-f}$ ) para que no se produzca fatiga a vida infinita, esto es a más de $10^6$ ciclos, para una carga exterior de tracción que oscila desde cero hasta el valor $F$ .

Para calcular el fallo a fatiga, tenemos que determinar la tensión media ( $\sigma_m$ ) y alternante ( $\sigma_a$ ) sobre el tornillo. Para más información ver nuestro prontuario de Fatiga.

$\sigma_a = \Large \frac{\sigma_{max} - \sigma_{min}}{2} \normalsize$

$\sigma_m = \Large \frac{\sigma_{max} + \sigma_{min}}{2} \normalsize$

Con:

$\sigma_{min} = \Large \frac{P}{A}$

$\sigma_{max} = \Large \frac{P+F_b}{A}$

Tenemos que:

$\sigma_a = \Large \frac{(P+F_b)-P}{2A} \normalsize = \Large \frac{F_b}{2A} \normalsize = \Large \frac{C F}{2A}$

$\sigma_m = \Large \frac{F_b+P}{2A} \normalsize + \Large \frac{2P}{2A} \normalsize = \Large \frac{CF}{2A}\normalsize + \Large \frac{P}{A}$

Utilizando el criterio de Goodman para el cálculo a fatiga para vida infinita definido en nuestro prontuario de Fatiga:

$\Large \frac{\sigma_a}{S_e} \normalsize + \Large \frac{\sigma_m}{S_u} \normalsize = 1$

$P_{max-f} = S_u A - \Large \frac{CF}{2} \left(\frac{S_u}{S_e}\normalsize + 1 \right)$

(+34) 605 304 564