Velas de succión vs. Velas de rotor

Con el aumento del precio de los carburantes y la nueva legislación para la reducción de los gases de efecto invernadero, las compañías marítimas buscan soluciones alternativas que les ayuden en el ahorro de combustibles fósiles.

Durante el siglo XX se desarrollaron tecnologías basadas en el viento para la impulsión de embarcaciones que obedecían los principios de sustentación de los perfiles aerodinámicos, que cobran cada vez más sentido en nuestros días.

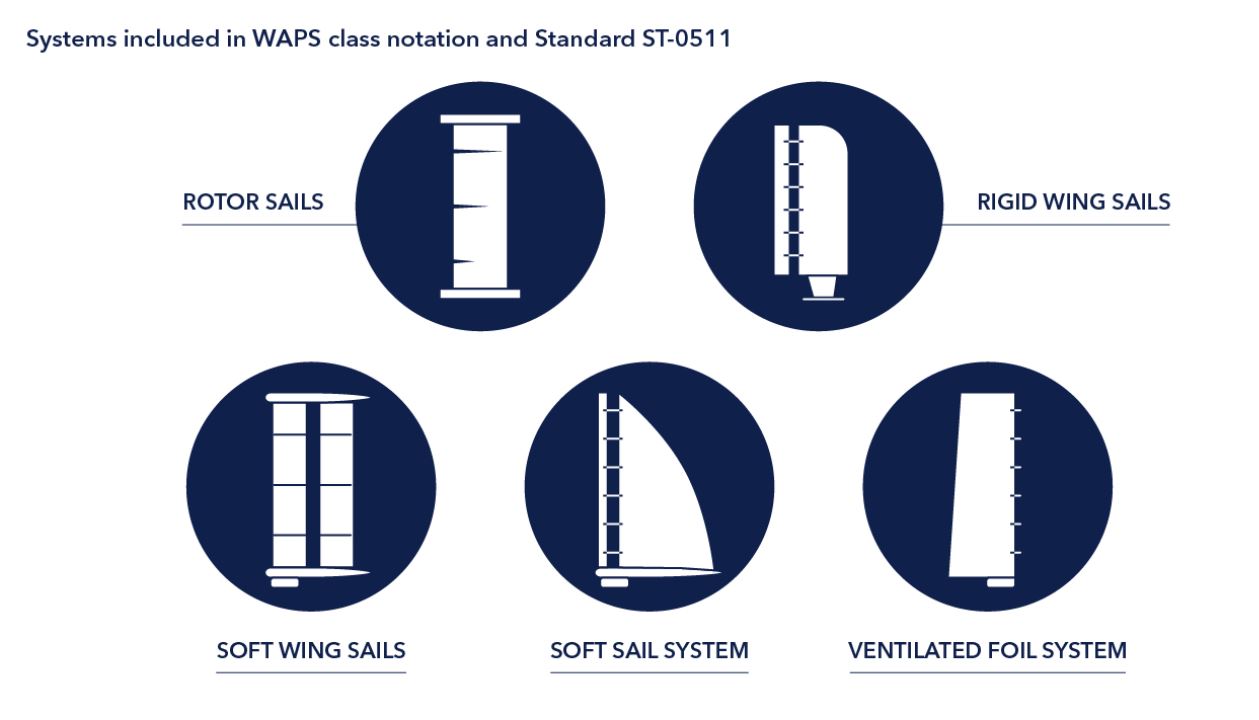
Las siguientes figuras muestran las diferentes tecnologías recogidas en el estándar de DNV ST-0511, junto con sus coeficientes de sustentación:

DNV Standard ST-0511

WAPS. Coeficientes de sustentación

Dichas tecnologías buscan generar la máxima fuerza de propulsión posible a través del viento sobre una estructura vertical (vela rígida) que alineada con la dirección de avance de la embarcación reduzca el uso de combustible en el motor general del barco.

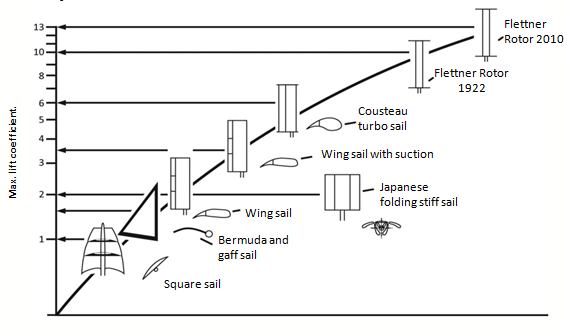
Existen tecnologías basadas en perfiles aerodinámicos con coeficientes de sustentación bajos y de gran superficie expuesta al viento para producir la fuerza de impulsión. Otras en cambio tienen una superficie pequeña, pero con un coeficiente de sustentación elevado que se consigue por medio de un mecanismo activo para adherir la capa límite que rodea la geometría de la vela rígida.

Estas últimas, los rotores Flettner y las velas de succión o turbovelas, dispuestas en la zona elevada de la figura debido a su elevado coeficiente de sustentación, son las más prometedoras ya que si las comparamos con las demás tecnologías, a igualdad de dimensiones son capaces de generar una mayor fuerza o, desde otro punto vista, generan la misma fuerza con un área expuesta al viento mucho más reducida por lo que la reducción de material y peso es muy significativa en ellas lo que les hace tener muchas ventajas y ser muy competitivas.

En cambio, necesitan una potencia adicional para adherir la capa límite del flujo de viento que las rodea en funcionamiento, de forma que si no se consigue esta adherencia el coeficiente de sustentación cae drásticamente y al no tener una superficie considerable la fuerza de propulsión producida cae de igual forma.

Principios aerodinámicos

Principios aerodinámicos de sustentación

La Aerodinámica es la parte de la mecánica de fluidos que estudia los fluidos en movimiento y las fuerzas o reacciones a las que están sometidos los cuerpos que se hallan inmersos en ellos.

Daniel Bernoulli comprobó experimentalmente que «en un fluido en movimiento, la suma de la presión y la velocidad en un punto cualquiera permanece constante». Por lo tanto, para que se mantenga esta constante, si una partícula aumenta su velocidad será a costa de disminuir su presión y viceversa.

El teorema de Bernoulli se suele expresar de la siguiente forma:

$P_t = P_e + P_d = P_e + \Large \frac{1}{2} \normalsize \rho V^2 = cte$

Donde:

$P_t$ : presión total
$P_e$ : presión estática
$P_d$ : presión dinámica
$V$ : velocidad del fluido
$\rho$ : densidad del fluido

Por tanto, si colocamos un objeto plano un poco inclinado hacia arriba contra el viento, este producirá una sustentación. Un perfil aerodinámico, es un cuerpo que tiene un diseño determinado para aprovechar al máximo las fuerzas que se originan por la variación de velocidad y presión cuando este perfil se sitúa en una corriente de aire.

Los perfiles aerodinámicos pueden ser aplicados en la navegación marítima para propulsar embarcaciones, de modo que son instalados verticalmente en el buque de manera que pueden rotar u orientarse al viento con respecto a la dirección de avance del barco. Cuando se somete un perfil aerodinámico a un flujo de aire, como puede ser el viento, aparece una fuerza aerodinámica resultante, que varía en función del ángulo de ataque del mismo. Esta puede descomponerse en la fuerza de sustentación ( $F_l$ ) y la fuerza de resistencia aerodinámica ( $F_d$ ).

Teorema de Bernoulli

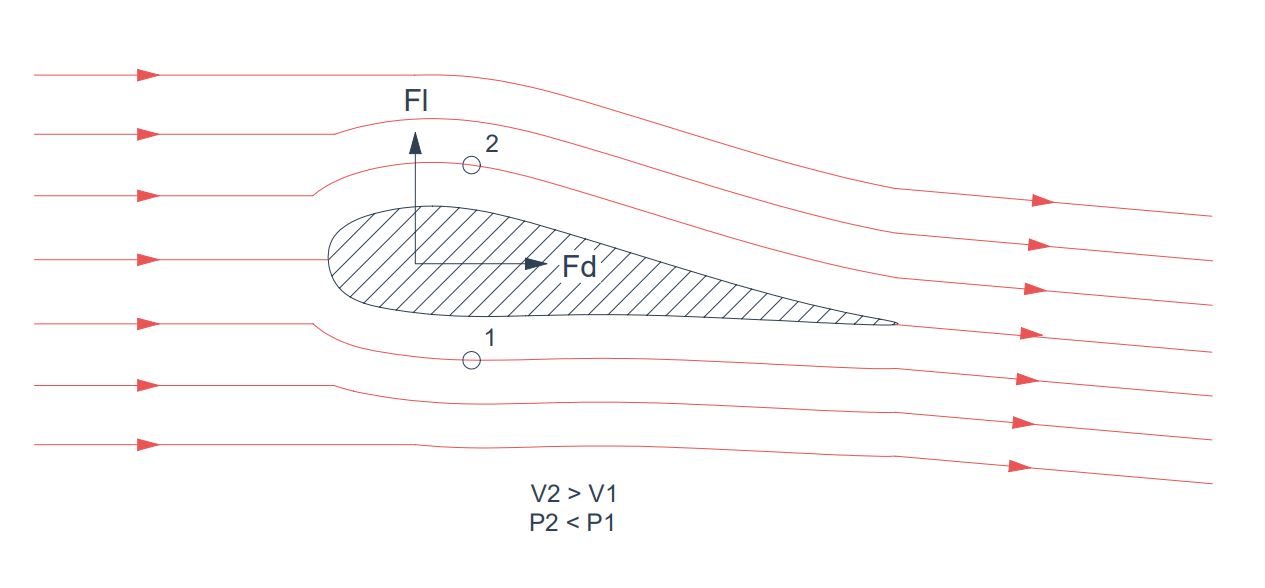
La sustentación ( $F_l$ ) es la fuerza desarrollada por un perfil aerodinámico al moverse a través de un fluido como diferencia de presiones ejercidas sobre su geometría y cuya dirección es perpendicular a la del fluido. Como con otras fuerzas aerodinámicas, en la práctica se utilizan coeficientes adimensionales que representan la efectividad de la forma de un cuerpo para producir determinadas fuerzas y se usan para facilitar los cálculos, diseños y comparativas entre perfiles.

Se define la fuerza de sustentación ( $F_l$ ), como la integral de las fuerzas de presión y fricción extendida a toda la superficie del perfil según la perpendicular a la dirección del viento.

$F_l = \oint_S (p-p_0) n_y dA + \oint_S (\bar{\bar{\tau}} · \vec{n})_y dA$

Así mismo, se define la fuerza de resistencia ( $F_d$ ), como la integral de las fuerzas de presión y fricción extendida a toda la superficie del perfil según la paralela a la dirección del viento.

$F_d = \oint_S (p-p_0) n_x dA + \oint_S (\bar{\bar{\tau}} · \vec{n})_x dA$

Dado que estas integrales son difíciles de resolver analíticamente, los perfiles aerodinámicos se ensayan en túneles de viento para extraer un coeficiente adimensional que sustituyera dichas integrales. Así, el coeficiente de sustentación ( $C_l$ ) y el de resistencia ( $C_d$ ) sirven para comparar la fuerza de sustentación y la fuerza de resistencia de manera rápida e intuitiva entre las diferentes geometrías de perfiles sin tener la necesidad de tener en cuenta la velocidad del fluido ni el tamaño de su geometría. Por esta razón, cualquier geometría puede escalarse para poder medirse en un túnel de viento, simplemente tiene que conservar su forma, pero no su tamaño.

Vela de succión

Las turbovelas o velas de succión fueron desarrolladas por Jacques Cousteau en los años 80, inspiradas en los rotores flettner. Esta vela rígida tiene forma cilindroide y evita el desprendimiento de la capa límite por medio de la aspiración parcial de la capa límite en la zona de sotavento a través de dos superficies perforadas. Dispone de un flap móvil que cambia de posición de forma simétrica si el viento viene desde babor o estribor para dirigir la dirección de la sustentación hacia la línea de avance de la embarcación, que además proporciona la estanqueidad en la superficie perforada que no se encuentra trabajando.

Sección de una turbosail

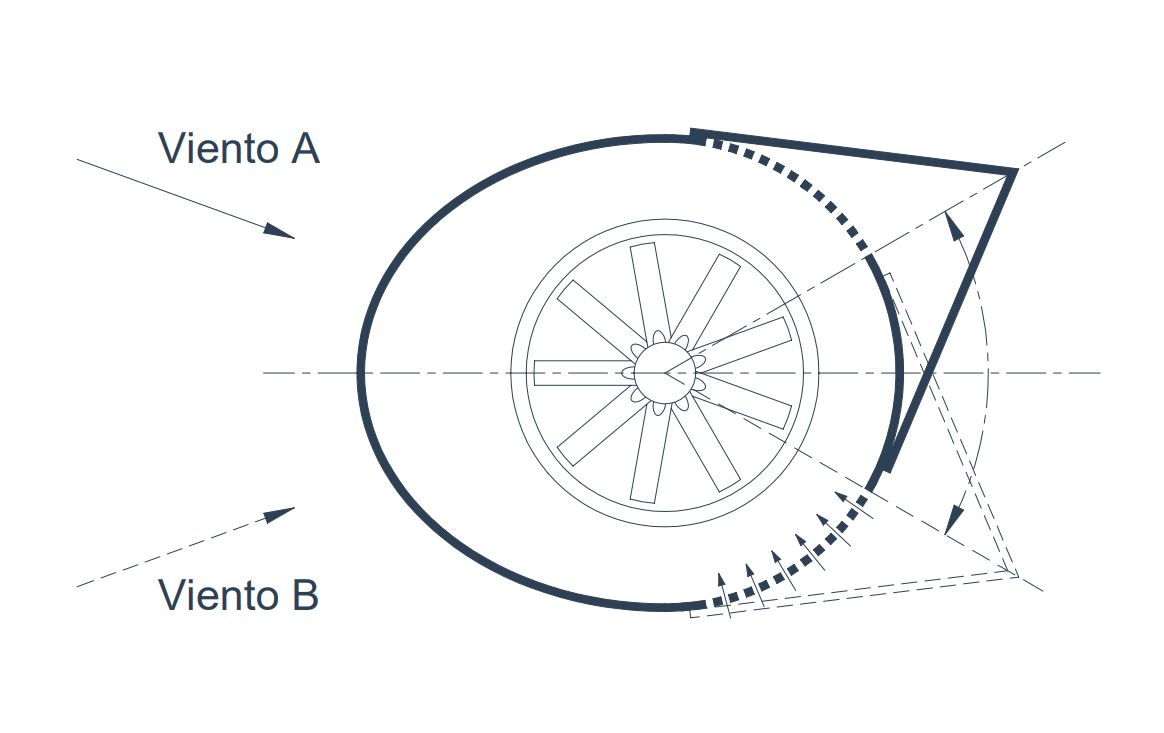
En un cuerpo cilindroide expuesto al viento, se produce un desprendimiento de la capa limite a en un determinado punto de su superficie que depende de las características del flujo y su número de Reynolds, principalmente. Si se aspira parte del flujo por la zona perforada de sotavento por medio de un caudal ( $Q$ ), el flujo se adhiere aumentando la fuerza de sustentación ( $F_l$ ) por medio de un incremento de su coeficiente adimensional ( $C_l$ ), que alcanza valores alrededor de 6 cuando comienza la adherencia.

Cousteau instaló dos velas de succión en el barco Alcyone, de 31 metros de eslora, con las siguientes características:

Longitud característica ( $L_c$ ): 2.05m
Altura ( $H$ ): 10.2m
Potencia de aspiración: 18kW

Alcyone

Para la sección de las velas de succión de Cousteau, se expone a continuación la gráfica que relaciona el coeficiente de sustentación ( $C_l$ ) con respecto al coeficiente de aspiración ( $C_Q$ ), adimensionalizados de la siguiente forma:

$C_Q = \Large \frac {Q}{V L_c}$

$C_l = \Large \frac {F_l}{\frac{1}{2} \rho V^2 L_c}$

Donde:

$Q$ : caudal de aspiración [m³/s]
$V$ : velocidad del viento [m/s]
$L_c$ : longitud característica [m]
$F_l$ : Fuerza de sustentación [N]
$\rho$ : densidad del aire [kg/m³]

Gráfica CQ-Cl

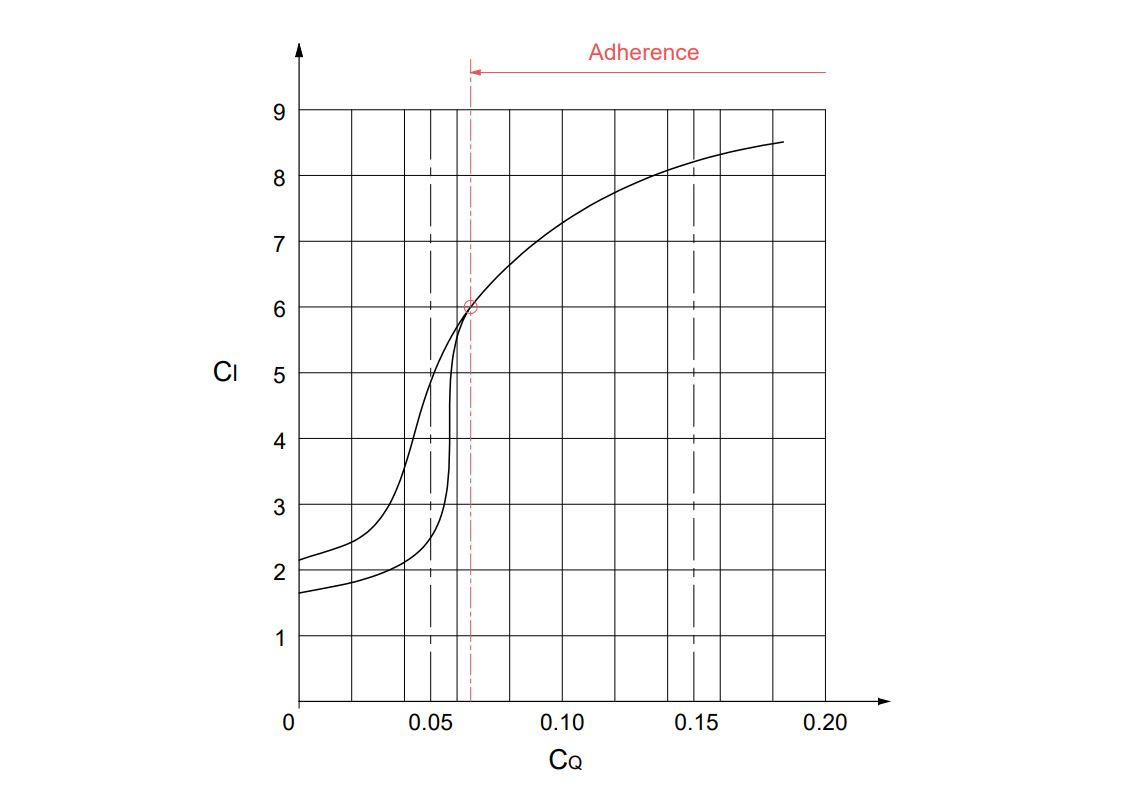
Este tipo de vela tiene la particularidad de que se alcanzan considerables a partir de un determinado. Si no se aspira con este caudal mínimo, el coeficiente de sustentación cae significativamente.

Obviando las pérdidas aerodinámicas tridimensionales, se tiene que, para la vela de Cousteau trabajando con un viento de media de 10m/s, el caudal necesario para conseguir la adherencia del flujo principal a través de toda la superficie perforada es de:

$Q = V L_c C_Q H = 10 · 2.05 · 0.064 · 10.2 = 13.4 \large \frac{m^3}{s}$

Con $H$ como la altura de aspiración, que se hace coincidir con la altura de la vela y suponiendo que el flujo de aspiración es el mismo para todas las secciones de dicha altura.

A este caudal de aspiración le corresponde la siguiente fuerza de sustentación:

$F_l = \Large \frac{1}{2} \normalsize \rho V^2 L_c C_l H = \Large \frac {1}{2}\normalsize 1.225 · 10^2 · 2.05 · 6 · 10.2 = 7684N$

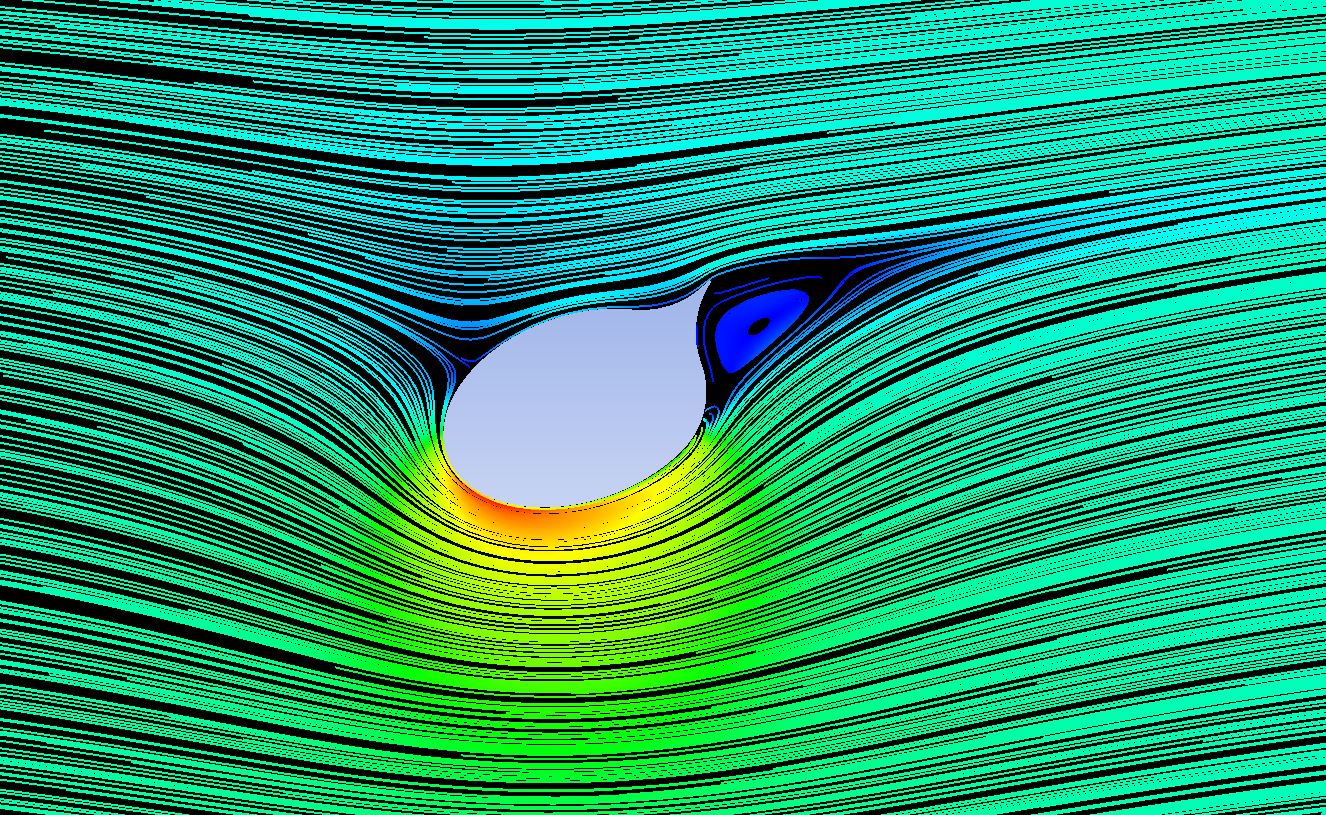
A continuación, se muestra una simulación CFD de la vela sección de la vela de Cousteau trabajando sin y con aspiración.

Turbosail sin aspiración

Una geometría cilindroide genera vórtices alternantes en la superficie de sotavento, produciendo una estela que produce fuerzas alternantes sobre la geometría. En el momento en el que se empieza a aspirar el flujo se adhiere, aumentando la velocidad sobre la cara inferior de la vela, bajando su presión de acuerdo con el teorema de Bernoulli.

Comienzo de la aspiración

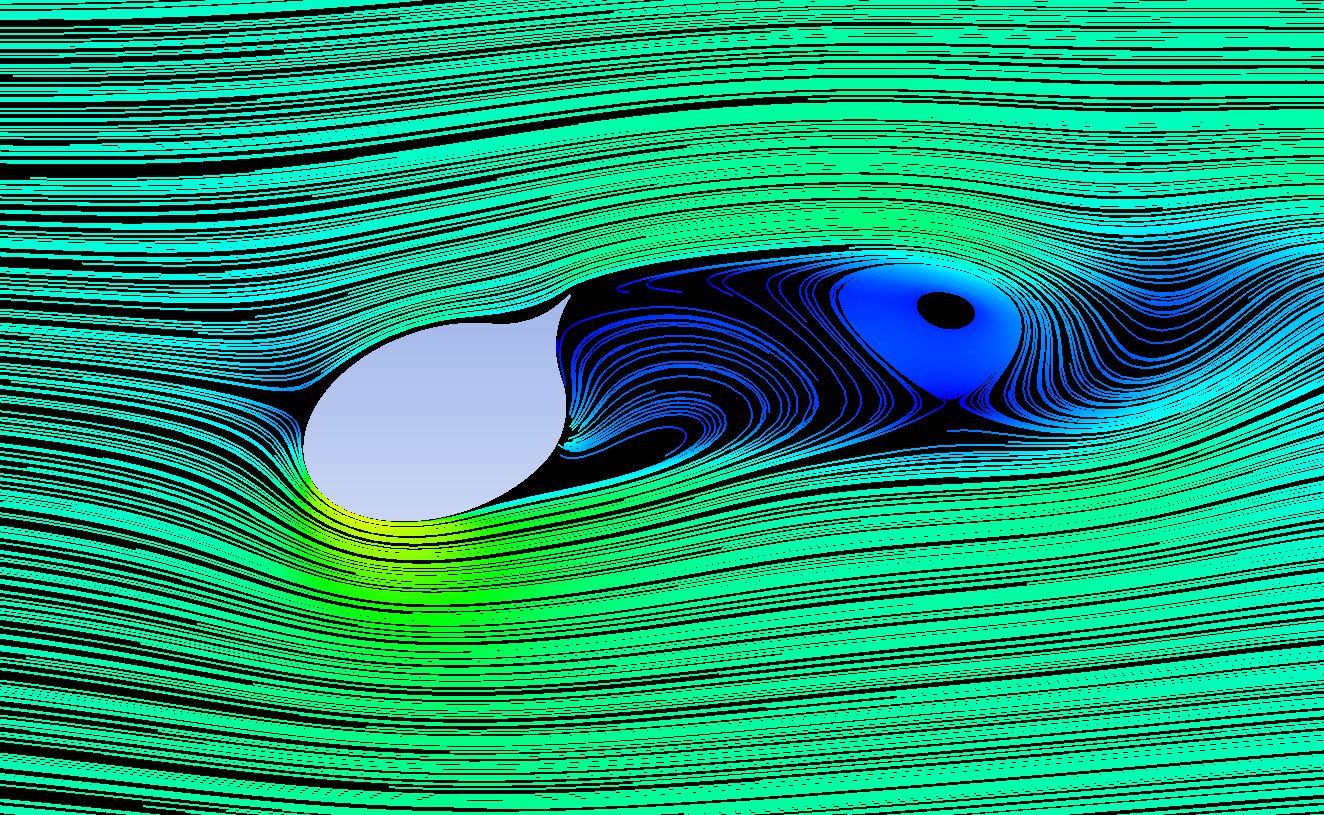
La integral estas presiones negativas sobre la superficie hace elevar el coeficiente de sustentación, y por lo tanto la fuerza o impulso de la vela. Además, esta última configuración aerodinámica, con un equilibrio aerodinámico sin vórtices alternantes, produce fuerzas de sustentación constantes a lo largo del tiempo.

Turbosail con aspiración de adherencia en equilibrio aerodinámico

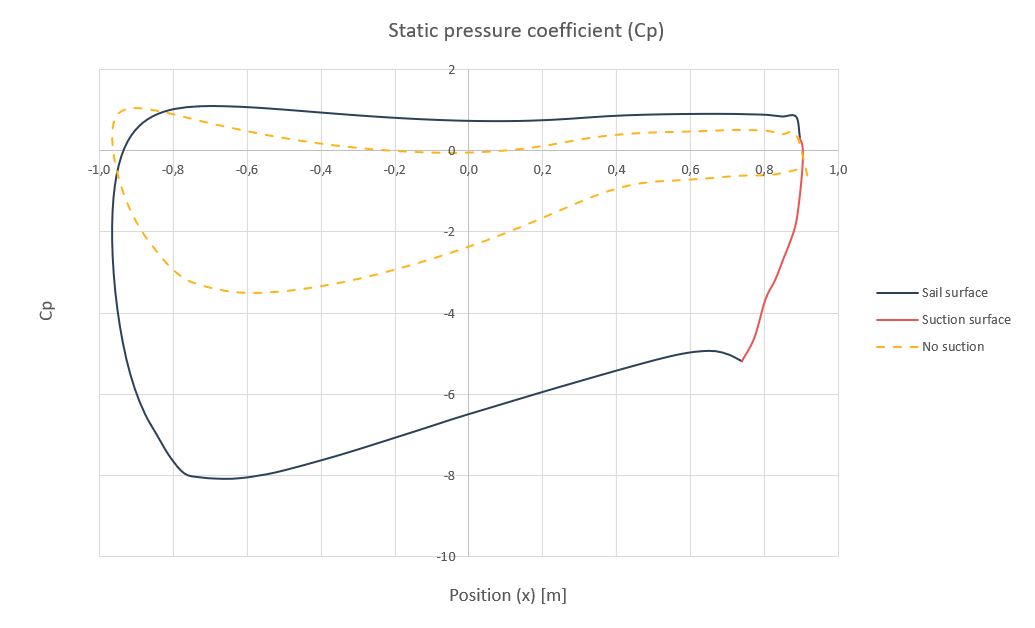
La siguiente gráfica muestra el coeficiente adimensional de la presión estática ( $C_p$ ) sobre la geometría de la vela en el punto de adherencia del flujo.

$C_p = \Large \frac{p}{\frac{1}{2} \rho V^2}$

Siendo:

$p$ : presión estática sobre la superficie de la vela
$\rho$ : densidad el viento
$V$ : velocidad del viento

De acuerdo con los párrafos anterior, integral de las curvas del coeficiente de presión ( $C_p$ ) nos proporcionan los coeficientes de sustentación ( $C_l$ ). Como puede observarse las curvas de presión con succión genera integrales, o áreas bajo la curva, de valores más altos que las curvas de presión sin succión. Esta es la base del principio de funcionamiento de la vela de succión o turbovela de Cousteau.

Coeficiente de presión estática sobre la superficie de la turbovela

Variación en los parámetros de diseño

La longitud característica ( $L_c$ ) y altura de la vela ( $H$ ) son dos parámetros que una vez que fabrica la vela no cambian, son parámetros fijos por diseño. Un aumento o disminución de estos parámetros es directamente proporcional a un aumento o disminución del caudal necesario para adherir el flujo y directamente proporcional a la fuerza de sustentación que se genera.

La velocidad del flujo o del viento ( $V$ ) es un parámetro variable. Si la velocidad del viento crece, el caudal de aspiración para mantener el punto mínimo de adherencia debe crecer también proporcionalmente si no se quiere que se desprenda el flujo y caiga el coeficiente de sustentación drásticamente. La fuerza de sustentación depende cuadráticamente de la velocidad del flujo por lo que si la adherencia es conseguida la sustentación se ve incrementada de manera muy importante.

La clave del funcionamiento de la turbosail, pasa por la afirmación condicional “si la adhesión es conseguida”.

Fijado el caudal y presiones máximas del ventilador de succión por diseño, junto con los parámetros mencionados anteriormente, longitud característica ( $L_c$ ) y altura de la vela ( $H$ ) existe una velocidad de viento máxima ( $V_{max}$ ) por encima de la cual, las velas de succión son incapaces de adherir el flujo, ya que no son capaces de generar el caudal de aspiración a la presión necesaria para ello.

Pérdidas de carga y Potencia

Un factor esencial que determina la potencia del ventilador de succión es la perdida de carga. En una vela de succión hay tres perdidas de carga a tener en cuenta:

Pérdida de carga en la superficie perforada de aspiración (Δp_asp)

La pared perforada por donde se aspira parcialmente el flujo se encuentra en la zona de sotavento de la vela donde la presión exterior es negativa. Si la presión interior de la pared proporcionada por el ventilador de succión justo al otro lado de la superficie perforada no es inferior a dicha presión el flujo nunca pasará desde fuera hacia adentro. En nuestro prontuario “Pérdida de carga en placas delgadas perforadas” se puede aproximar esta pérdida energética de acuerdo con los parámetros que intervienen en dicho cálculo.

En nuestro prontuario Pérdidas de carga en placas delgadas perforadas se puede aproximar esta pérdida energética de acuerdo con los parámetros que intervienen en dicho cálculo.

Pérdida de carga por cambio de dirección del flujo de aspiración (Δp_dir)

La entrada de flujo en la vela a través de la superficie perforada es horizontal, mientras que se aspira con un ventilador dispuesto en vertical en la parte superior de la vela. El cambio de dirección que debe hacer el flujo desde que entra en la vela hasta que llega al ventilador supondrá una pérdida de carga a tener en cuenta en el diseño.

Pérdida de carga por las diferencias de altura en las zonas de aspiración (Δp_h)

Dado que el ventilador está en la parte superior de la vela, las pérdidas de carga serán mayores cuanto más separadas estén las zonas de aspiración de dicho ventilador, siendo la más desfavorable la sección de aspiración en la parte inferior de la vela.

La potencia hidráulica ( $W_h$ ) necesaria para adherir el flujo puede determinarse por:

$W_h = | p | \cdot Q$

donde $Q$ es el caudal necesario para la adherencia del flujo, supuesto constante en cada sección de la superficie de aspiración, y $p$ es la presión necesaria a la entrada del ventilador de succión, que puede expresarse como:

$p = p_{ext} - \Delta p_{asp} - \Delta p_{dir} - \Delta p_h$

Donde $p_{ext}$ es la presión en el exterior de la superficie de aspiración y siempre es negativa.

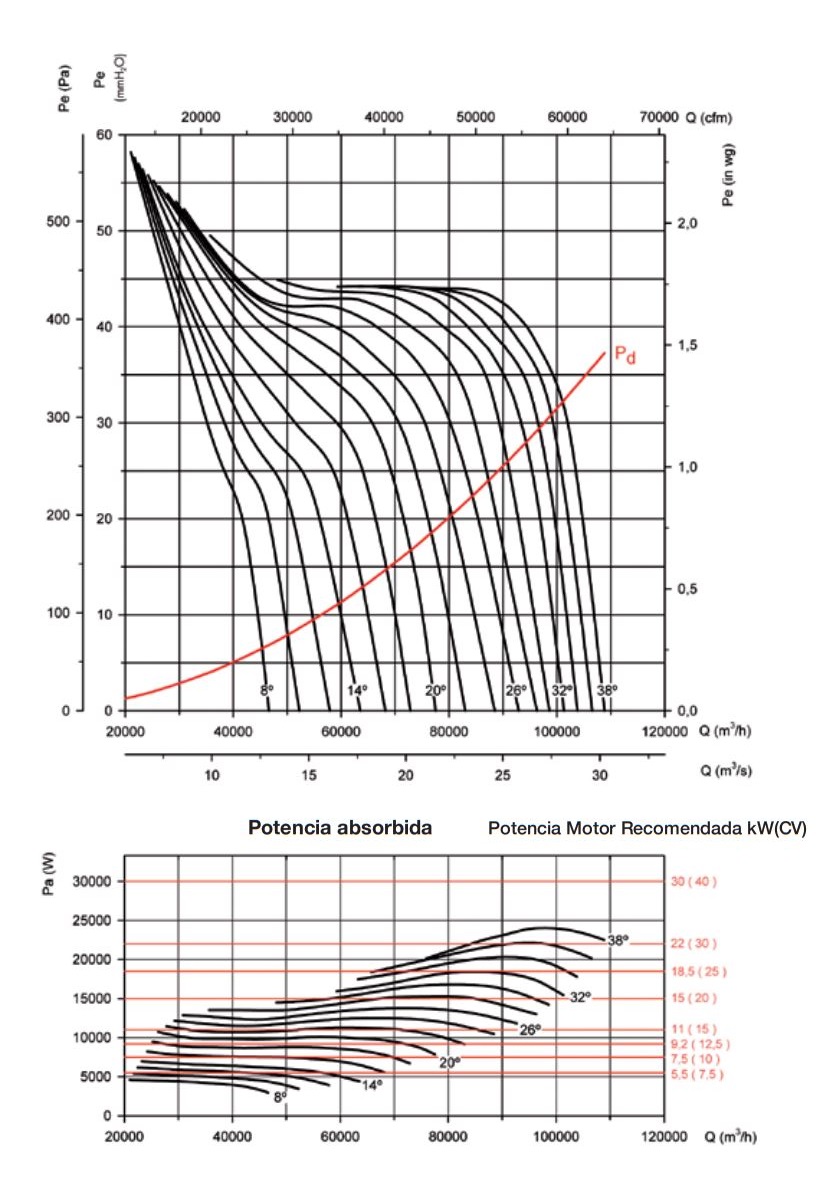
Dado que el ventilador es movido por un motor eléctrico existe un rendimiento a la hora de pasar de la potencia hidráulica ( $W_h$ ) a la potencia eléctrica ( $W_e$ ), por lo que los fabricantes de ventiladores proporcionan la relación entre presión y caudal con la potencia eléctrica que suministra un ventilador específico.

Ventilador. Características técnicas

Vela de rotor

En 1853 el físico y químico alemán Heinrich Gustav Magnus identifica el efecto que lleva su nombre a través de la rotación de objetos dentro de un fluido en movimiento, donde la velocidad tangencial o periférica del objeto se suma o se resta a la del fluido dependiendo del punto del objeto que se analiza, creando un flujo rotacional alrededor del cuerpo y produciendo una fuerza sustentadora.

Efecto Magnus

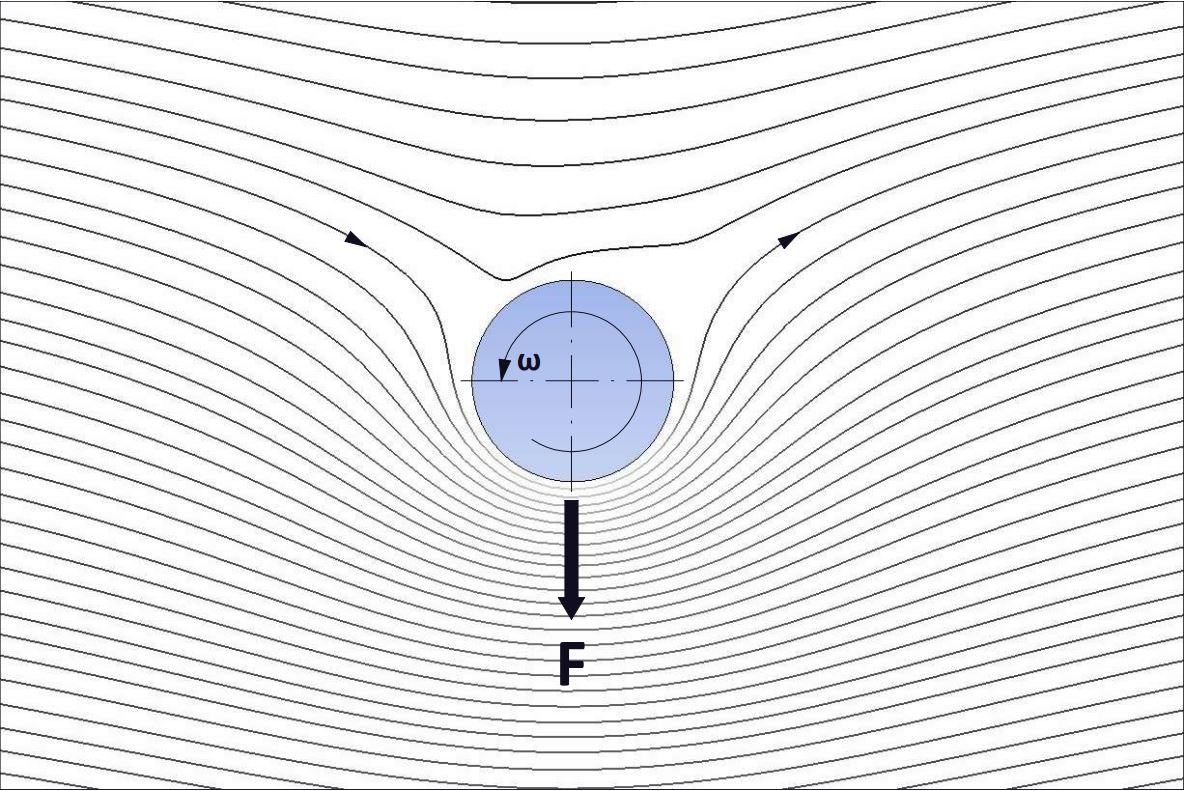
Por lo tanto, para producir una fuerza de sustentación ( $F_l$ ), con su correspondiente coeficiente de sustentación ( $C_l$ ), la sección de la columna cilíndrica debe ser rotada a una velocidad significativa ( $\omega$ ) y adimensionalizada a través del coeficiente de velocidad tangencial o periférica ( $C_{\omega}$ ):

$C_{\omega} = \Large \frac{\omega L_c}{2 V}$

$C_l = \Large \frac{F_l}{\frac{1}{2}\rho V^2}$

Donde:

$C_{\omega}$ : coeficiente de velocidad
$L_c$ : longitud característica coincidente con el diámetro de la vela
$\omega$ : velocidad angular
$V$ : velocidad del flujo de viento
$C_l$ : coeficiente de sustentación
$\rho$ : densidad del fluido
$F_l$ : fuerza de sustentación

En los años 20 del siglo pasado, Anton Flettner asistido por el ingeniero Ludwig Pandtl, entre otros, inventa el rotor que lleva su nombre para la impulsión de embarcaciones. Las velas de rotor o rotores Flettner aprovechan el efecto Magnus para adherir el flujo a una sección perfectamente cilíndrica en rotación.

Ludwig Prandtl

(Freising, 1875 – Göttingen, 1953)

Ingeniero y físico alemán, especializado en la teoría de la aerodinámica, la mecánica de fluidos y el comportamiento mecánico de los materiales. Desarrolló la base matemática que da sustento a los principios fundamentales de la aerodinámica subsónica. El número de Prandtl, que relaciona la viscosidad cinemática con la difusividad térmica, ha sido nombrado en su honor.

El siguiente video muestra la adhesión del flujo en la sección circular del rotor por medio de la rotación de la misma. Se trata, por tanto, de un mecanismo muy diferente a la hora de adherir el flujo si lo comparamos con las velas de succión.

En 1923, el Instituto de Investigación Aerodinámica (AVA) de Göttingen determina experimentalmente los coeficientes de arrastre ( $C_d$ ) y sustentación ( $C_l$ ) del rotor en función de las velocidades constantes del flujo de entrada, que constituyen la base para los cálculos de dichos sistemas. Estos estudios se ampliaron en 1985 por el ISF de Hamburgo, con nuevos ensayos de túneles de viento para caracterizar las terminaciones de los rotores con discos de varios diámetros, además de reafirmar los coeficientes ya existentes.

Se expone, a continuación, la gráfica de los coeficientes de sustentación ( $C_l$ ) con respecto al coeficiente de velocidad tangencial ( $C_{\omega}$ ).

Coeficiente de sustentación (Cl)

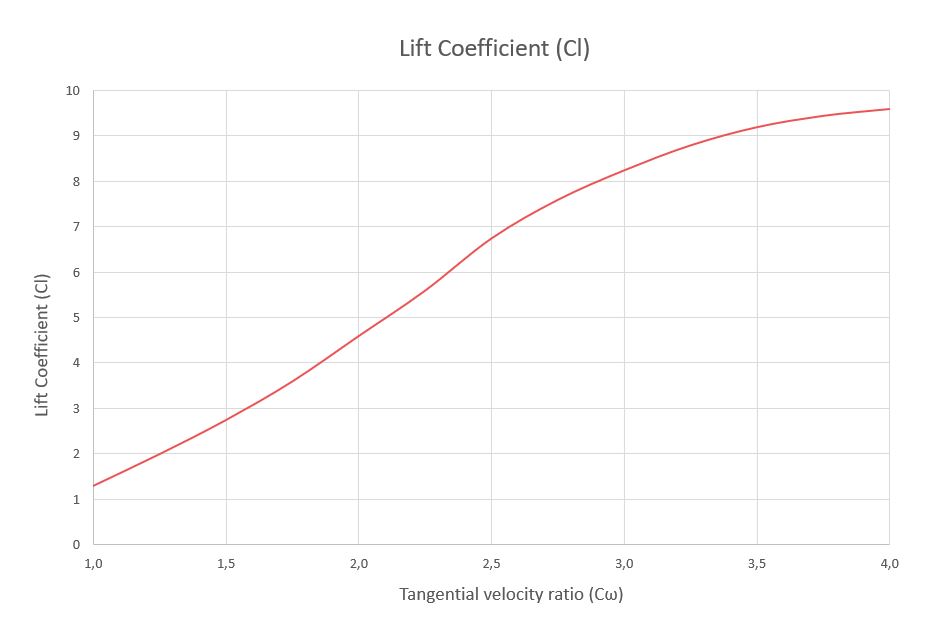
De acuerdo con los resultados, el comportamiento óptimo del rotor se consigue cuando el coeficiente de velocidad tangencial alcanza el valor de 4, punto en el que la configuración de presiones estáticas sobre la geometría de la vela se vuelve simétrica.

Coeficiente de presión (Cp) para Lc = 1

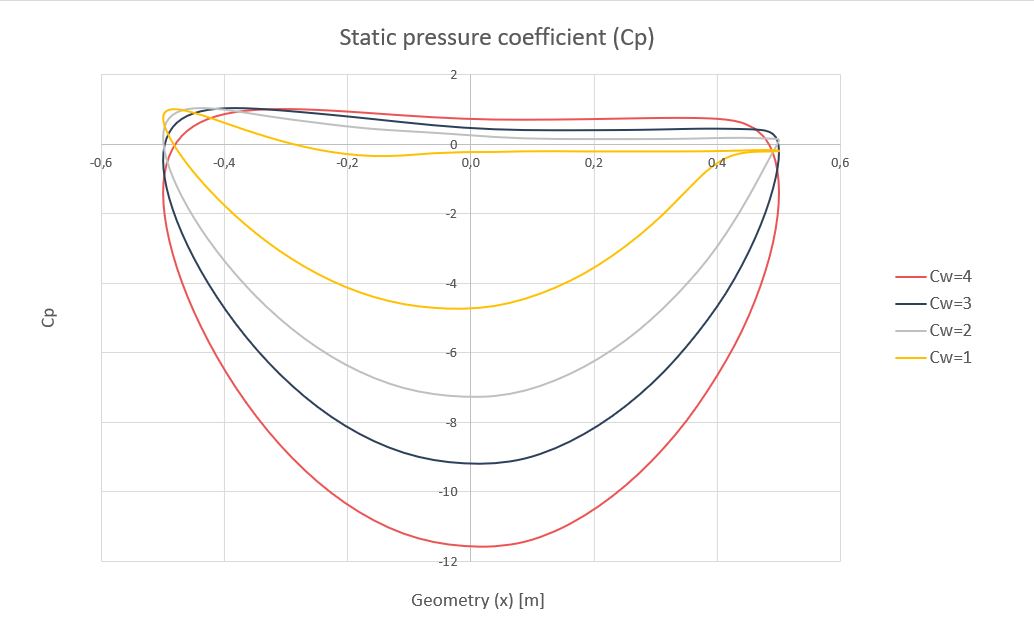
Del mismo modo, la relación de aspecto ( $\large \frac{H}{L_c}$ ) debe ser también superior a este valor para obtener ratios elevados entre el coeficiente de sustentación y el de resistencia (coeficiente de planeo, ε). En la actualidad este valor se encuentra alrededor de 7.

Los discos de cierto tamaño en los extremos de la vela también permiten mejorar el comportamiento tridimensional, elevando los coeficientes.

Así, barcos como el Buckau o el RMS Barbara fueron adaptados para estos rotores durante los años 20 del siglo pasado con resultados de impulso muy satisfactorios. En la actualidad el E-ship es un RoLo de carga que se impulsa con la ayuda de esta tecnología. Comparamos algunas de sus características:

	Buckau	RMS Barbara	E-ship
Nº rotors	2	10	4
Diameter [m]	2.8	4	4
Height [m]	16	17	27
Angular speed [rpm]	125	160	300
Power/rotor [kW]	10	30	100
Ship length [m]	45	85	130

Familias de rotores

Debido a que los mecanismos de rotación tienen que mover la vela completa, la velocidad de rotación ( $\omega$ ) está limitada principalmente por las fuerzas inerciales que se alcanzan en la geometría cilíndrica.

A continuación, se muestran una tabla con valores aproximativos de las velocidades máximas de rotación ( $\omega_{max}$ ) dependiendo del diámetro o longitud característica ( $L_c$ ) de la misma:

Lc [m]	ω [rpm]
2	450
3	300
4	225
5	180

De acuerdo con estos valores, para velocidades de viento elevadas, el coeficiente de velocidad tangencial no siempre podrá llegar al valor óptimo de 4, por lo que los coeficientes de sustentación estarán por debajo del máximo (9.6).

Del coeficiente de velocidad tangencial ( $C_{\omega}$ ) se puede deducir que los rotores que tienen la misma velocidad tangencial ( $V_t$ ) se comportan de la misma forma frente a la magnitud de la velocidad del fluido ( $V$ ).

$V_t = \Large \frac{1}{2} \normalsize \omega_{max} L_c$

Son las llamadas familias de rotores. Cuando éstos aumentan de tamaño ( $Lc$ ), conservan su comportamiento y coeficientes aerodinámicos disminuyendo la velocidad máxima de giro ( $\omega_{max}$ ).

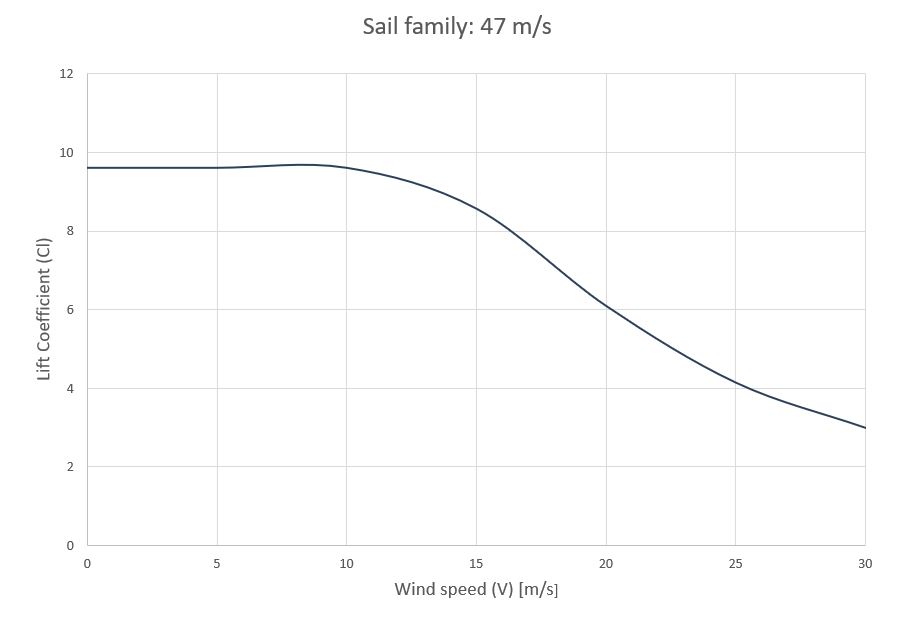
La gráfica siguiente muestra el descenso del coeficiente de sustentación ( $C_l$ ) con respecto a la velocidad de viento ( $V$ ) para la familia 47 m/s.

Familia 47m/s

Turbo vs. Rotor

Mecanismo de adherencia

Las velas de rotor adhieren el flujo de forma mucho más eficiente que las velas de succión. Mientras que el primero utiliza la rotación mecánica de la vela completa, el segundo lo hace aspirando desde el interior a través de una superficie perforada en la zona de sotavento. La aspiración es menos eficiente ya que parte de la energía se pierde en pérdidas de carga. Esto no ocurre con las velas de rotor, ya que el mecanismo de adherencia no tiene perdidas de eficiencia con la altura de la vela al ser puramente mecánico.

Condiciones de adherencia del flujo

Las velas de rotor empiezan a adherir el flujo prácticamente de forma continua a medida que se aumenta la velocidad de rotación aumentando su coeficiente de sustentación progresivamente. Las velas de succión no empiezan a tener un coeficiente de sustentación considerable hasta alcanzar un caudal mínimo de aspiración.

Orientación al viento

La vela de succión debe ser orientada en la dirección del viento para producir los coeficientes de sustentación descritos, por lo que necesitará un sistema de control que conozca la dirección del viento en cada instante. La vela de rotor, al tratarse de una sección axi-simétrica en los dos ejes, no necesita este sistema de control de orientación, solo necesita controlar su rotación.

Fuerzas generadas para la misma longitud característica

Las fuerzas de sustentación que generan ambas velas para longitudes características bajas, en torno a 2, y velocidades de viento bajas, en torno a 10m/s, son ligeramente superiores para las velas de rotor. Al subir dicha velocidad y/o la longitud característica, y debido a que el sistema para adherir el flujo no es eficiente en velas de succión, éstas no podrán generar sustentación más allá de su velocidad de viento máxima de diseño. En cambio, las velas de rotor pueden seguir generando sustentación, aunque a un coeficiente menor que el máximo. Este descenso del coeficiente de sustentación se ve compensado por la velocidad cuadrática del viento.

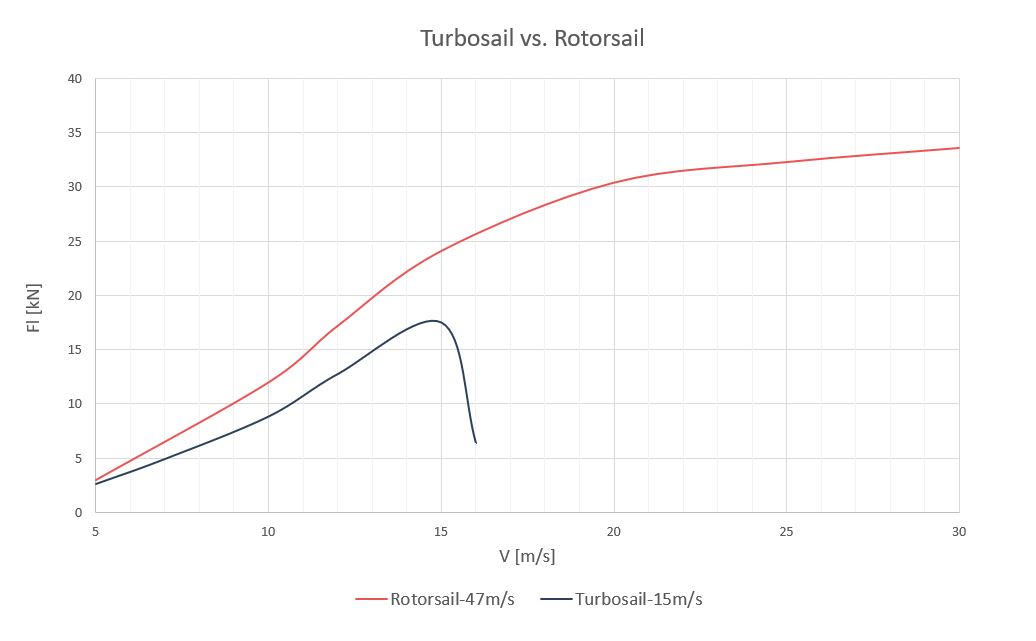
A continuación, se muestra una gráfica donde se comparan las fuerzas de sustentación para una turbovela, cuya velocidad máxima de flujo es de 15m/s, y una vela de rotor, ambas, con una longitud característica de 2m y una altura de 10.2m (configuración del Alcyone de Cousteau).

Turbo vs. Rotor. Lc = 2m, H = 10.2m

Escalabilidad con la longitud caraceterística (Lc)

Las velas de succión parecen tener limitado el crecimiento de su longitud característica en torno a 2 metros (Alcyone). Al aumentar este parámetro, el ventilador necesario para adherir el flujo empieza a ser enorme debido principalmente al aumento del valor absoluto de la presión negativa en la cara exterior de la superficie de succión a sotavento, alcanzándose presiones muy altas con caudales medios, por lo que se empieza a tener problemas a la hora de instalar ventiladores comerciales. En cambio, las velas de rotor al aumentar su longitud característica, requieren una disminución de la velocidad angular de rotación, lo que hace que decrezca su coeficiente de sustentación pero que compensan con la adherencia a altas velocidades de flujo de viento.

Escalabilidad con la altura (H)

Ambas tecnologías no parecen tener problemas con coeficientes de aspecto (λ) en torno a 5. Las velas de rotor llegan hasta 7, aumentando su altura sin ningún tipo de condición adicional. Las velas de succión también pueden hacerlo si se aumenta, a priori, el caudal de succión proporcionalmente con la nueva altura.

$\lambda = \Large \frac{H}{L_c}$

Resumen

En resumen, la velas de succión parecen tener limitado su tamaño a una geometría similar a la que se dispuso en el Alcyone, por lo que no son capaces de generar los grandes impulsos que necesitan los grandes buques de más de 40 metros de eslora.

La velas de rotor se muestran más versátiles que las velas de succión abarcando un rango bastante amplio de fuerzas de impulsión. Si bien para barcos de corta eslora ambas podrían entrar en competencia para velocidades de viento inferiores a 10-15 m/s, las velas de succión no pueden ni siquiera hacerles sombra en la impulsión de grandes buques, debido principalmente a su ineficiencia técnica a la hora de adherir el flujo para conseguir una sustentación significativa.

(+34) 605 304 564