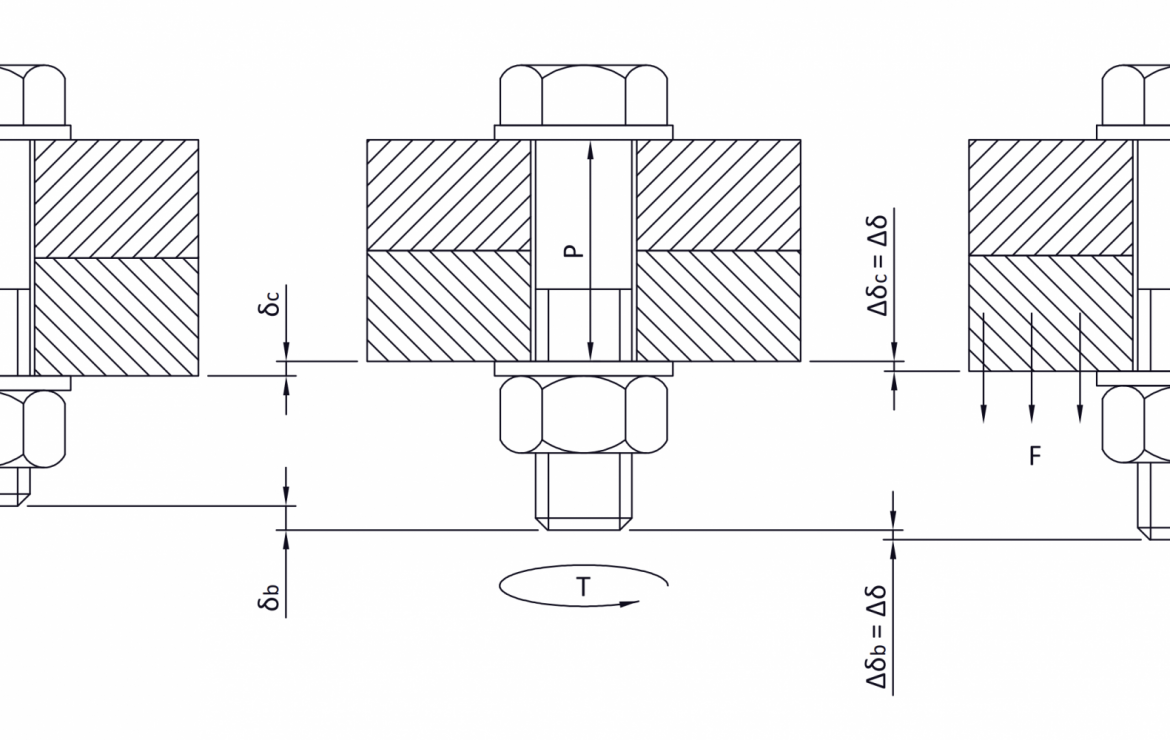
Tensile stress in preloaded bolts

A preloaded bolt joining two or more parts is subjected to a preloading force ( $P$ ) which is used to elongate the bolt ( $P_b$ ) and compress the connecting elements ( $P_c$ ).

$P = P_b + P_c$

Preload and strain in bolts

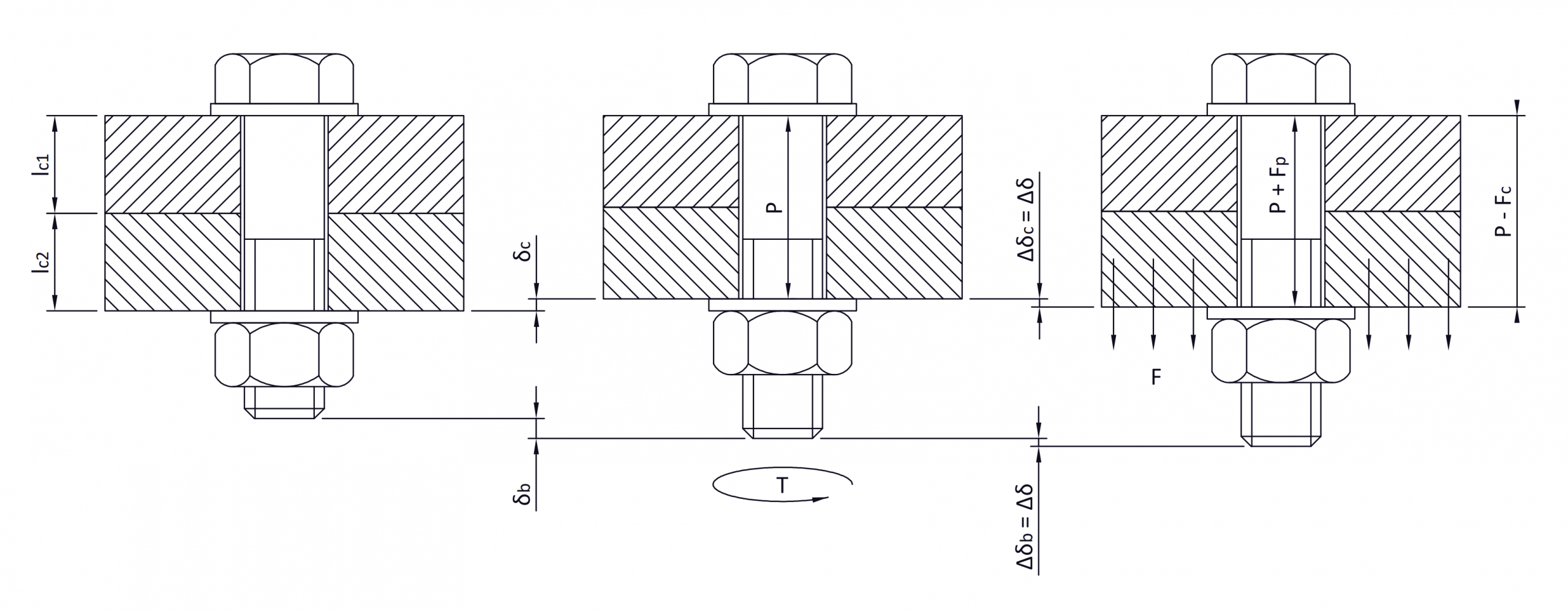
When a preloading force is applied, the bolt deforms a positive length ( $\delta_b$ ), it lengthens, and in the same time, the connecting parts deform a negative length ( $\delta_c$ ), they shorten.

$\delta_b = \Large \frac{P_b}{K_b}$

$\delta_c = \Large \frac{P_c}{K_c}$

Where:

$K_b$ : bolt stiffness constant
$K_c$ : stiffness constant of the joining parts

Preload graph

When an external load ( $F$ ) is applied through the joint parts, the bolt elongates again by a new shifting ( $\Delta \delta_b$ ) due to a force $F_b$ and the parts are to decompress by a negative shift ( $-\Delta \delta_c$ ) caused by a force $F_c$ .

Since the joint is in state of equilibrium it follows that:

$F = F_b + F_c$

$\left | \Delta \delta_b \right | = \left | \Delta \delta_c \right | = \Delta \delta$

Applying the equations relating load to displacement in the elastic domain, we have that:

$\Delta \delta_b = \Large \frac{F_b}{K_b}$

$\Delta \delta_c = \Large \frac{F_c}{K_c}$

Substituting:

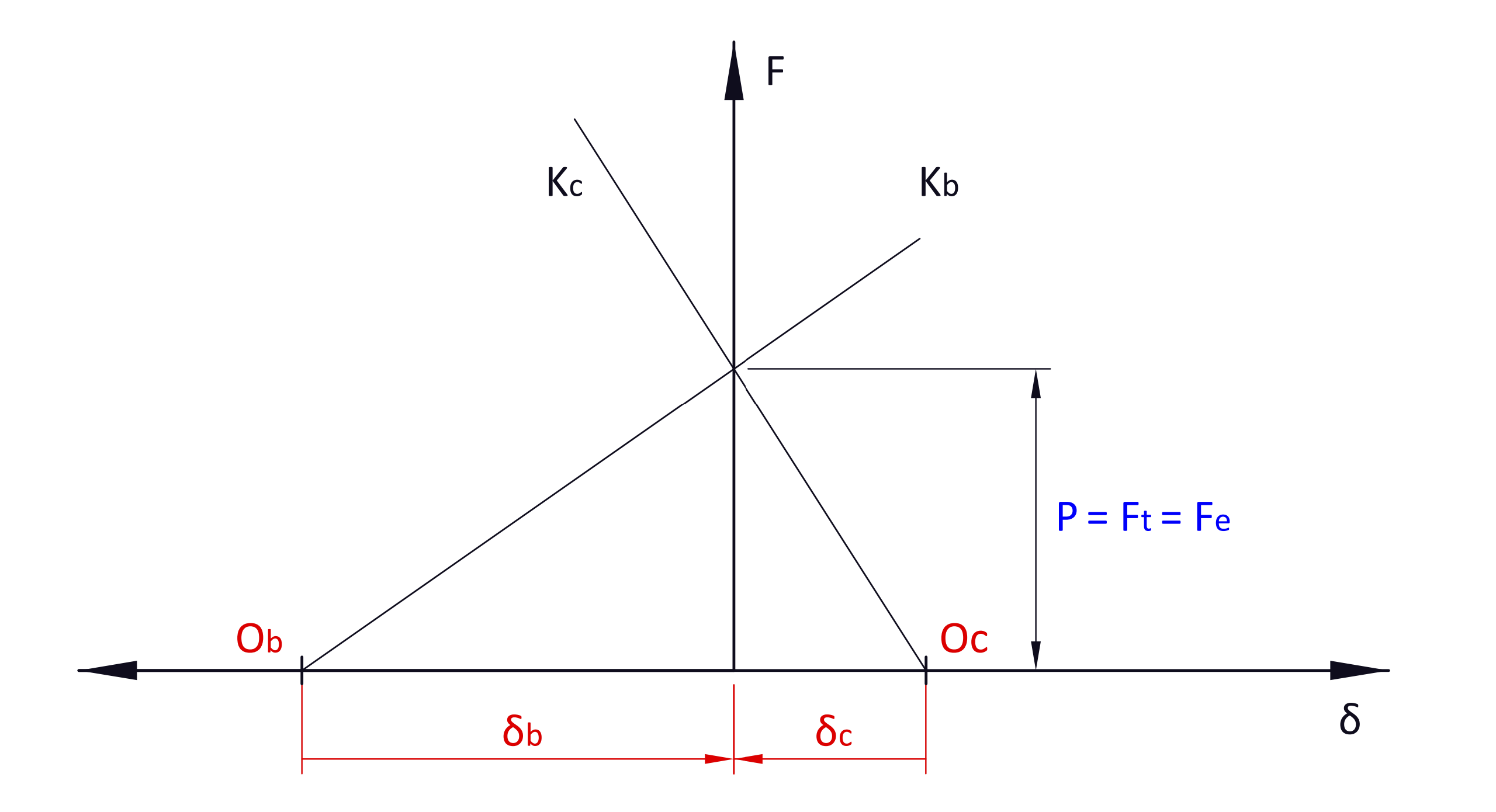
$\Delta \delta = \Large \frac{F_b}{K_b} \normalsize = \Large \Large \frac{F_c}{K_c}$

$F_b = K_b \Large \frac{F_c}{K_c}\normalsize = K_b \Large \frac{F-F_b}{K_c}$

$F_b = \Large \frac{K_b}{K_b+K_c}\normalsize F = C F$

With $C$ as the joint stiffness constant:

$C = \Large \frac{K_b}{K_b+K_c}$

In analogy for $F_c$ we have that:

$F_c = \Large \frac{K_c}{K_b+K_c}\normalsize F = (1- C) F$

To calculate the joint stiffness constant ( $C$ ), we must first determine the bolt stiffness constant ( $K_b$ ) and the joint element stiffness constant ( $K_c$ ). In our post Preloaded bolted joint stiffness the reader can find estimations of these parameters.

Applying an external force to preload bolts

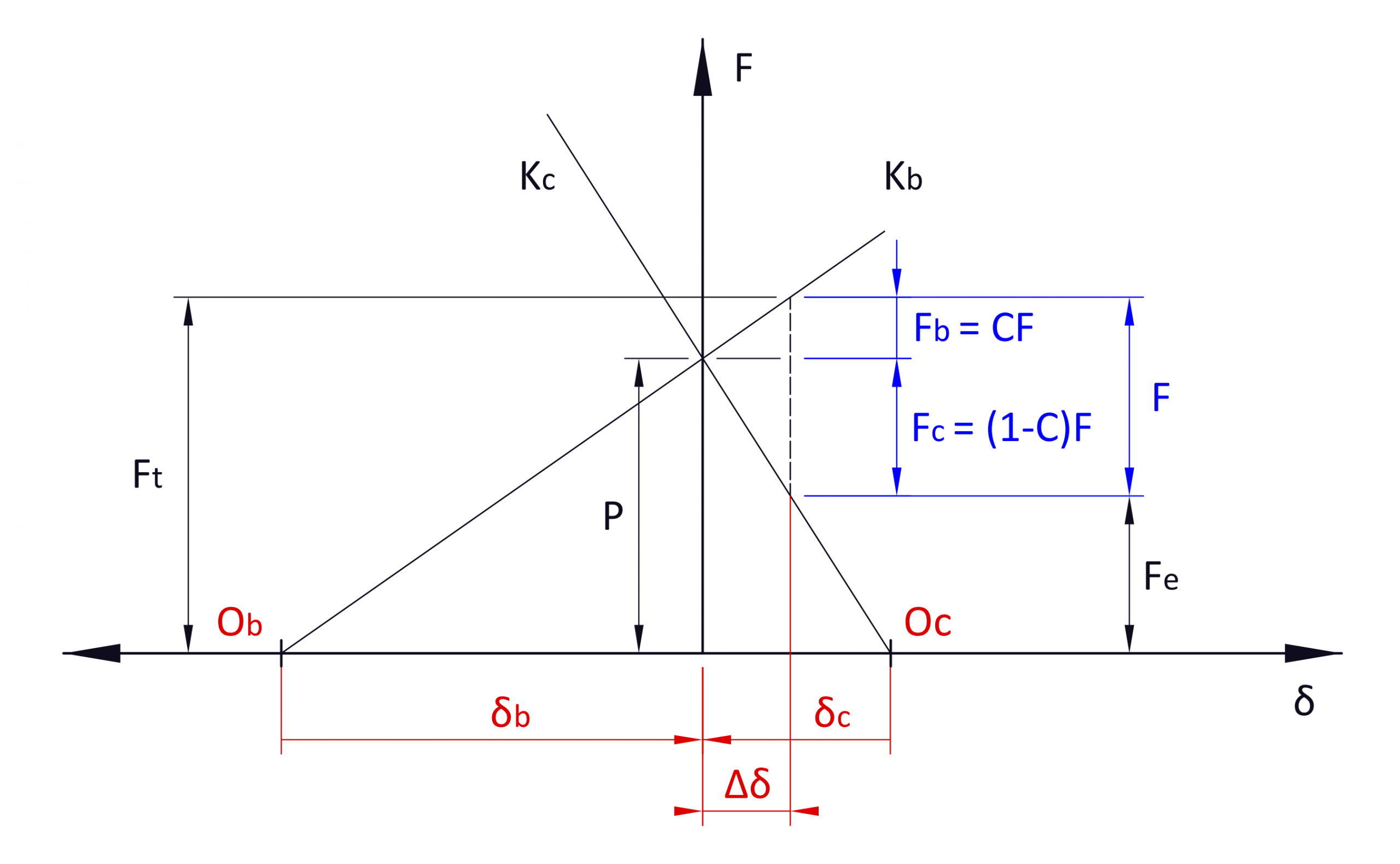
The final load on the bolt ( $F_t$ ) and on the connecting elements ( $F_e$ ) after applying an external load ( $F$ ) with a preload ( $P$ ) are:

$F_t = P+CF$

$F_e = P-(1-C)F$

Preload

Normally a preload ( $P$ ) is selected between:

$P_{min} \leq 0.6 A S_y \leq P \leq 0.8 A S_y \leq P_{max}$

With high preload values so that the bolts do not tend to loosen due to vibration:

$P = 0.75 A S_y$

Grade	Yield limit (Sy) [MPa]	Tensile limit (Su) [MPa]
5.8	400	500
8.8	640	800
10.9	900	1000
12.9	1080	1200

Minimum preload
Maximum preload

Minimum preload

It is the minimum preload ( $P_{min}$ ) so that the separation of the joint elements due to the external tensile force ( $P$ ) does not occur. This condition is met when:

$\Delta \delta_c = \delta_c$

$\Large \frac{F_c}{K_c}\normalsize = \Large \frac{P_c}{K_c}$

$P_{min} = F_c = \Large \frac{K_c}{K_b+K_c} \normalsize F = (1-C)F$

Maximum preload

External static loads

It is the maximum preload that the bolt can withstand ( $P_{max-s}$ ) so that it does not reach its yield limit ( $S_y$ ) when it is working at a tensile load ( $F_b$ ), therefore:

$F_y = P_{max-s} + F_b$

$P_{max-s} = S_y A - C F$

Where:

$F_y$ : force in the yield limit
$A$ : bolt resistant section

Alternating loads in fatigue

It is the maximum preload that the bolt can withstand ( $P_{max-f}$ ) for fatigue to occur at infinite life, i.e. over $10^6$ cycles, for an external tensile load ranging from zero to the $F$ value.

To calculate the fatigue failure, we have to determine the mean ( $\sigma_m$ ) and alternating stress ( $\sigma_a$ ) on the bolt. For more information, please see our Fatigue handbook:

$\sigma_a = \Large \frac{\sigma_{max} - \sigma_{min}}{2} \normalsize$

$\sigma_m = \Large \frac{\sigma_{max} + \sigma_{min}}{2} \normalsize$

With:

$\sigma_{min} = \Large \frac{P}{A}$

$\sigma_{max} = \Large \frac{P+F_b}{A}$

We have that:

$\sigma_a = \Large \frac{(P+F_b)-P}{2A} \normalsize = \Large \frac{F_b}{2A} \normalsize = \Large \frac{C F}{2A}$

$\sigma_m = \Large \frac{F_b+P}{2A} \normalsize + \Large \frac{2P}{2A} \normalsize = \Large \frac{CF}{2A}\normalsize + \Large \frac{P}{A}$

Using Goodman’s criterion in the fatigue calculation for infinite life defined in our Fatigue handbook:

$\Large \frac{\sigma_a}{S_e} \normalsize + \Large \frac{\sigma_m}{S_u} \normalsize = 1$

$P_{max-f} = S_u A - \Large \frac{CF}{2} \left(\frac{S_u}{S_e}\normalsize + 1 \right)$

(+34) 605 304 564