La importancia de la rigidez en seguidores solares
Se tiende a pensar que el amortiguamiento (ξ) es un valor crítico a la hora de un análisis aeroelástico de un seguidor a un eje, y esta afirmación es cierta sobre todo en el comportamiento frente al galope, pero la importancia de la rigidez en seguidores solares es tan grande que cualquier otro parámetro a su lado parece insignificante.
Si analizamos esta afirmación cualitativamente, las estructuras de gran rigidez permanecen estáticas, sin una deformación considerable, frente al viento que actúa sobre ellas, por lo que, la incorporación de amortiguamiento no tendría sentido ya que no hay un movimiento que atenuar.
No existe ninguna estructura infinitamente rígida por lo que ingeniería debe considerar si los movimientos producidos por el viento se pueden considerar dentro del cálculo estático o, en cambio, se debe pasar a un análisis dinámico, como es el caso de seguidores a un eje con un mecanismo central.
Se puede considerar que la rigidez a torsión de un seguidor viene dada enteramente por su tubo de torsión sin cometer errores significativos en el cálculo. Si suponemos que el viento actúa sobre el seguidor como un momento distribuido a lo largo de cada tubo de torsión, tenemos que:
- El máximo giro ( \phi_{max} ) se encuentra en la sección más alejada del mecanismo y depende de los siguientes parámetros:
\phi_{max} = \Large \frac{m L^2}{2GJ}
Donde:
-
- \phi_{max} : ángulo máximo girado de la sección en radianes
- m: momento distribuido a lo largo del tubo de torsión
- L: longitud del tubo de torsión
- G: módulo de cizalladura del material
- J: módulo de torsión de la sección
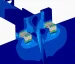
- La máxima tensión tangencial debida a la torsión ( \tau_{max} ) se encuentra en la sección más cercana al mecanismo. En de una sección cuadrada de pared delgada, la tensión tangencial es nula en los vértices del cuadrado y máxima en la mitad de los lados.
\tau_{max} = \Large \frac{m L}{2eA_m}
Donde:
- \tau_{max} : tensión tangencial máxima por torsión
- e : espesor de la pared del tubo de torsión
- A_m : área que encierra la línea media de la pared del tubo de torsión
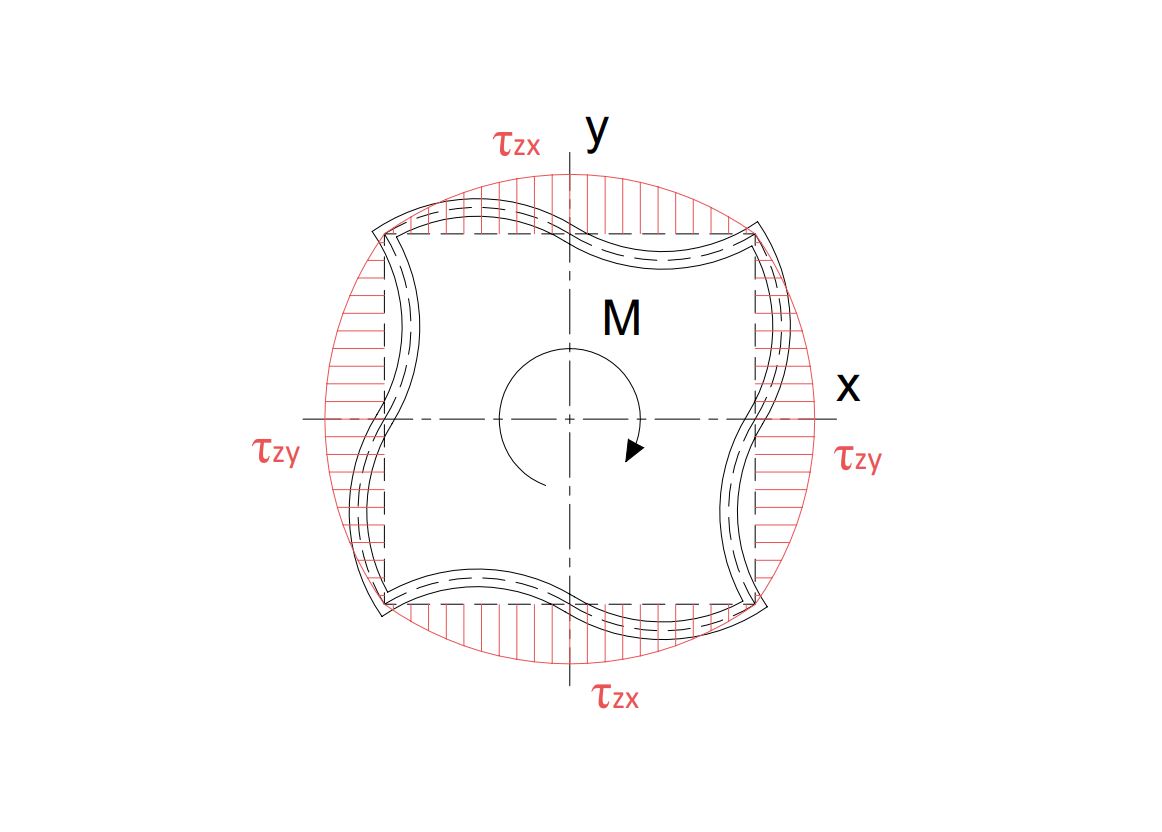
La mejor sección para soportar la torsión es uno circular macizo, pero debido a su alto coste no se emplea en este tipo de estructuras. El siguiente candidato es el perfil circular de pared delgada, aunque se emplea en algunos seguidores, se prefiere el perfil cuadrado hueco porque al tener cuatro planos facilita el montaje de elementos sobre él.
El módulo de torsión de la sección (J) para un perfil cuadrado de pared delgada tiene la expresión que viene dada por la fórmula de Bredt:
J = e(d-e)^3
Donde e y d son el espesor de la pared y el lado exterior del tubo de torsión respectivamente.
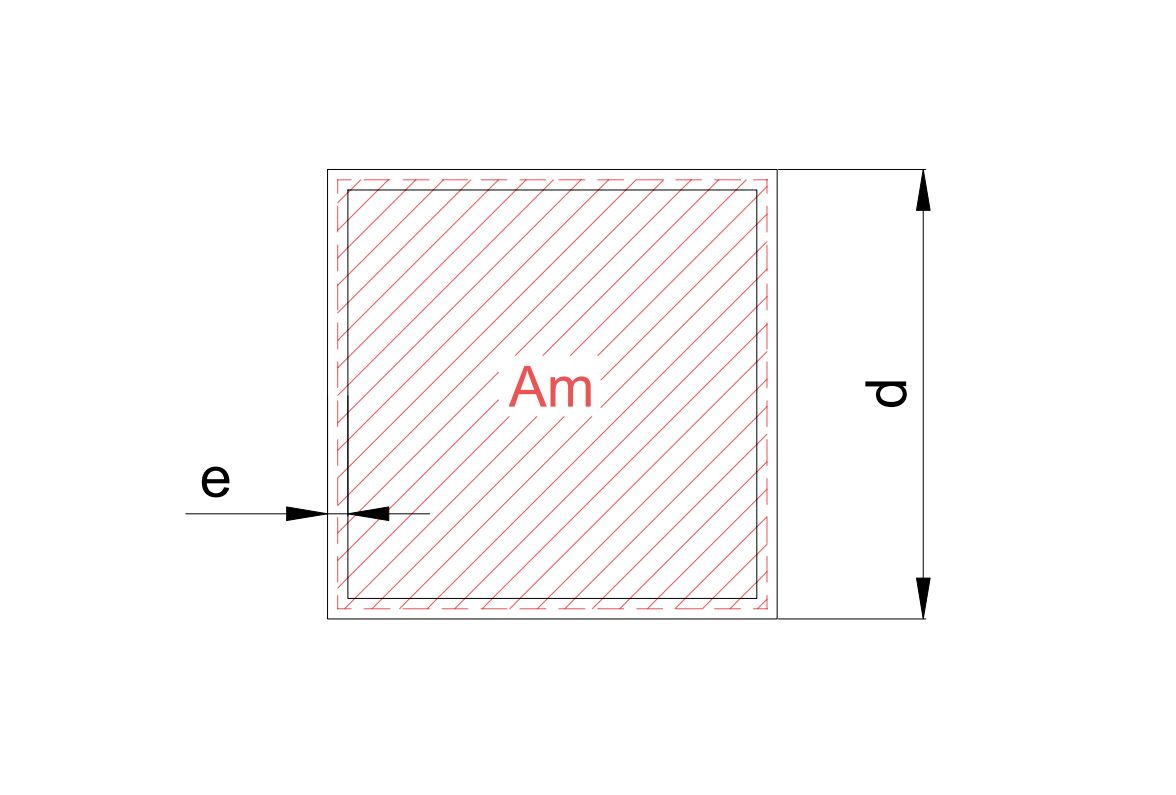
Por otro lado, el área que encierra la línea media del espesor del perfil ( A_m ) es:
A_m = (d-e)^3
Escribiendo de nuevo las expresiones de tensión y giro máximos para cada tubo de torsión, tenemos que:
\phi_{max} = \Large \frac{m L^2}{2Ge(d-e)^3}
\tau_{max} = \Large \frac{m L}{2e(d-e)^2}
Ambas expresiones se relacionan a través de los momentos distribuidos como:
\Large \frac{\tau_{max}}{\phi_{max}} \normalsize = \Large \frac{G(d-e)}{L}
También es posible deducir una rigidez distribuida (k) que será muy útil en el cálculo computacional CFD bidimensional.
k = \Large \frac{m}{\phi} \normalsize = \Large \frac{2Ge(d-e)^3}{L^2}
En vista a estas fórmulas simples se puede calcular el momento distribuido máximo admisible para la sección de una geometría dada y una longitud determina, así como la deflexión máxima para dichos momentos.
Se han tomado las tres cuartas partes del límite elástico admisible ( f_y ) del material (Acero S355JR) ya que existen otros esfuerzos de flexión y cortante que hay que considerar en el tubo de torsión:
\Large \frac{3}{4} \normalsize f_y > \sigma_{VM} = \sqrt{3} \tau_{max} = \sqrt{3} \Large \frac{mL}{2e(d-e)^2}
Con \sigma_{VM} como la tensión de Von Mises, y de donde se puede escribir el momento máximo distribuido como:
m < \Large \frac{2e(d-e)^2}{\sqrt{3}L} \frac{3}{4} \normalsize f_y
Se exponen a continuación los momentos distribuidos admisibles para tubos de torsión con las siguientes longitudes y secciones:
| Section | m max [Nm/m] | |||
|---|---|---|---|---|
| #140.5 | 2666 | 1439 | 1083 | 869 |
| #210.5 | 6146 | 3319 | 2498 | 2003 |
| #250.5 | 8779 | 4741 | 3568 | 2861 |
| #300.5 | 12728 | 6873 | 5173 | 4147 |
| L [m] | 9.5 | 17.5 | 23.3 | 29.1 |
Para estos momentos máximos, se exponen los giros máximos de la última sección.
| Section | ф max [º] | |||
|---|---|---|---|---|
| #140.5 | 6.90 | 12.77 | 16.97 | 21.17 |
| #210.5 | 4.54 | 8.41 | 11.18 | 13.94 |
| #250.5 | 3.80 | 7.04 | 9.35 | 11.66 |
| #300.5 | 3.16 | 5.85 | 7.77 | 9.69 |
| L [m] | 9.5 | 17.5 | 23.3 | 29.1 |
Si el momento distribuido sobre el seguidor calculado mediante estudios CFD o ensayos de túneles de viento es mayor que los admitidos por nuestro tubo de torsión marcados en la tabla anterior, el tubo colapsará por tensiones tangenciales.
Rigidez vs Divergencia torsional
En nuestro post de divergencia en seguidores solares una rigidez mínima ([/latex] = k_{div} ) es necesaria para evitar la divergencia torsional antes de alcanzar la velocidad de viento de supervivencia de la planta V_{surv,1h} = U = 30m/s:
k_{div} = \Large \frac{1}{2} \normalsize \rho U^2 b^2 \Large \frac {\partial C_m}{\partial \alpha}
Por lo que la rigidez en seguidores solares, definida por la geometría del tubo de torsión, debe ser mayor que la que marca este límite.
\Large \frac{2GJ}{L^2} \normalsize > \Large \frac{1}{2} \normalsize \rho U^2 b^2 \Large \frac {\partial C_m}{\partial \alpha}
| Section | k div30 | k [Nm/m rad] | |||
|---|---|---|---|---|---|
| #140.5 | 19087 | 22140 | 6456 | 3657 | 2351 |
| #210.5 | 19666 | 77525 | 22605 | 12806 | 8231 |
| #250.5 | 20001 | 132336 | 38587 | 21860 | 14051 |
| #300.5 | 20423 | 231018 | 67360 | 38162 | 24529 |
| L [m] | 9.5 | 17.5 | 23.3 | 29.1 | |
Los valores marcados en rojo indican una rigidez inferior a la necesitada para evitar la divergencia torsional para la sección y longitud de tubo marcados.
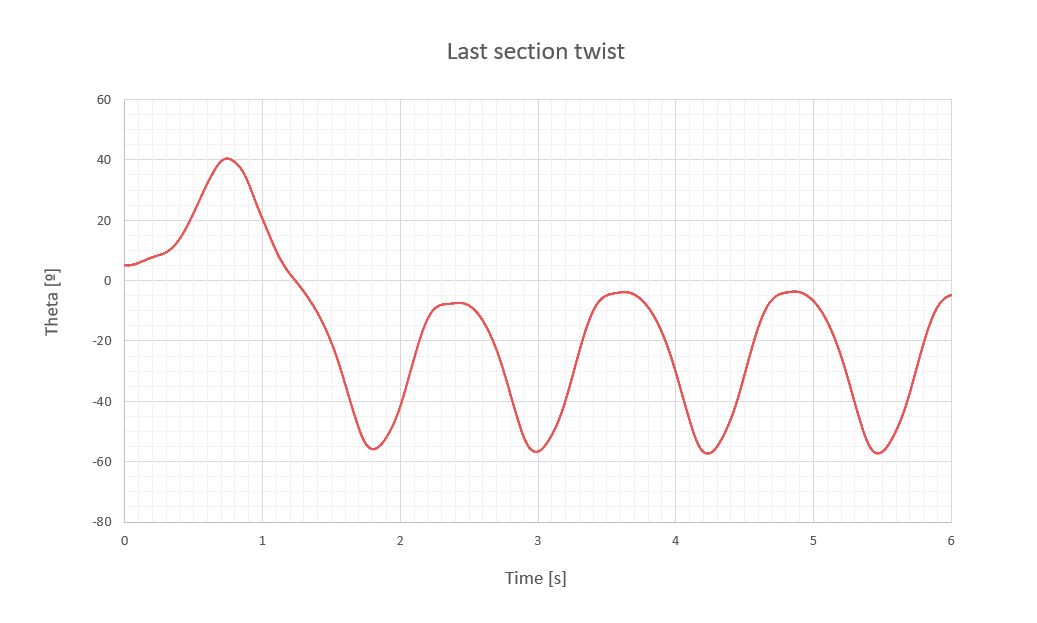
A continuación, se expone a modo de ejemplo los momentos calculados para un seguidor de un eje cuyos tubos de torsión miden 17.5m, 30 módulos a cada lado del mecanismo en dos filas de 15, con una sección #140.5, trabajando con la velocidad de supervivencia de la planta ( V_{surv,1h} = 30m/s ) con coeficiente de amortiguamiento de 0.25.
Según las tablas, la rigidez del tubo no cumpliría con la necesaria para salvar la divergencia torsional, pero además los momentos distribuidos alcanzados en la sección rebasarían el límite elástico del material, por lo que este tubo colapsaría ante las cargas dinámicas del viento de supervivencia, pudiendo o no acoplarse con fenómenos aeroelásticos de divergencia torsional, dependiendo de la velocidad del viento.
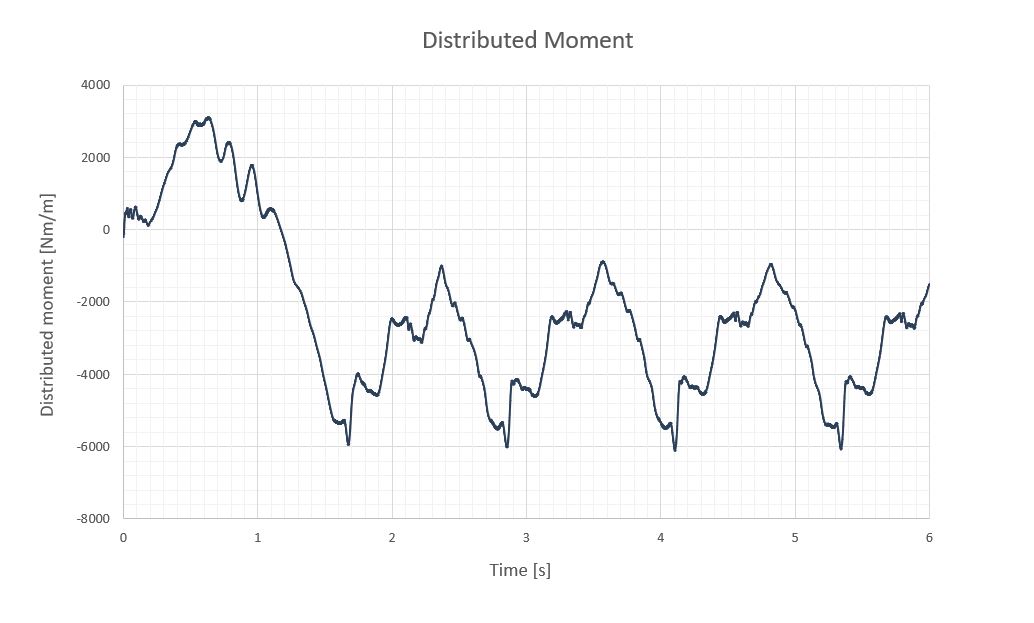
En este caso, el video no sería realista ya que el tubo de torsión colapsaría cuando se alcanzara los momentos distribuidos máximos admisibles, pero si no tuviéramos esta limitación en el material, el seguidor se deformarían grandes ángulos ante dichas cargas ya que su rigidez es pequeña frente a la energía que tiene el viento a la velocidad de supervivencia de la planta ( V_{surv,1h} = 30m/s )